Statystyka i model bayesowski: wyjaśnienie

Technika bayesowska to podejście w statystyce stosowane w analizie danych i estymacji parametrów. To podejście opiera się na twierdzeniu Bayesa.

Statystyka bayesowska opiera się na unikalnej zasadzie, w której pomaga określić łączny rozkład prawdopodobieństwa dla obserwowanych i nieobserwowanych parametrów przy użyciu modelu statystycznego. Znajomość statystyki jest niezbędna do rozwiązania problemów analitycznych w tym scenariuszu.

Od czasu wprowadzenia twierdzenia Bayesa w latach 70. XVIII wieku przez Thomasa Bayesa pozostaje ono nieodzownym narzędziem w statystyce. Modele bayesowskie są klasycznym zamiennikiem modeli częstościowych, ponieważ ostatnie innowacje w statystykach pomogły przekroczyć kamienie milowe w wielu branżach, w tym w badaniach medycznych, zrozumieniu wyszukiwań internetowych i przetwarzaniu języków naturalnych (przetwarzanie języka naturalnego).

Na przykład choroba Alzheimera jest chorobą, o której wiadomo, że stanowi postępujące ryzyko w miarę starzenia się osoby. Jednak za pomocą twierdzenia Bayesa lekarze mogą oszacować prawdopodobieństwo wystąpienia choroby Alzheimera w przyszłości. Dotyczy to również raka i innych chorób związanych z wiekiem, na które dana osoba staje się podatna w późniejszych latach życia.

Częste statystyki a statystyki Bayesa

Statystyka częsta kontra statystyka bayesowska stale była tematem kontrowersji i koszmarów dla początkujących, z których obaj mają trudności z wyborem między nimi. Na początku XX wieku statystyka bayesowska miała swój udział w problemach z nieufnością i akceptacją. Z czasem jednak ludzie zdali sobie sprawę z możliwości zastosowania modeli bayesowskich i dostarczanych przez nie dokładnych rozwiązań.

Oto przyjrzyjmy się częstym statystykom i związanej z nimi złożoności:

Częste statystyki

Jest to szeroko stosowana metodologia wnioskowania w świecie statystyki. Analizuje, czy zdarzenie (wymienione jako hipoteza) miało miejsce. Szacuje również prawdopodobieństwo wystąpienia zdarzenia w czasie trwania eksperymentu. Eksperyment powtarza się aż do osiągnięcia pożądanego rezultatu.

Ich próbki dystrybucji mają rzeczywistą wielkość, a eksperyment jest teoretycznie powtarzany nieskończenie wiele razy. Oto przykład pokazujący, jak często statystyki można wykorzystać do badania rzucania monetą.

• Możliwość zdobycia głowy przy jednorazowym rzucie monetą wynosi 0,5 (1/2).
• Liczba głowic oznacza rzeczywistą liczbę pozyskanych leadów.
• Różnica między rzeczywistą liczbą orłów a oczekiwaną liczbą orłów będzie się zwiększać wraz ze wzrostem liczby rzutów.

Tak więc tutaj wynik zależy od tego, ile razy eksperyment zostanie powtórzony. Jest to poważna wada częstych statystyk.

Inne wady związane z jego projektowaniem i technikami interpretacji stały się widoczne w XX wieku, kiedy stosowanie częstych statystyk do modeli numerycznych było u szczytu.

Ograniczenia częstych statystyk

Poniżej wymieniono trzy główne wady częstych statystyk:

1. Zmienne wartości p

Wartości p zmierzone dla próbki o stałej wielkości w eksperymencie ze zdefiniowanym punktem końcowym zmieniają się wraz ze zmianą punktu końcowego i wielkości próbki. Daje to dwie wartości p dla jednej niepoprawnej danych.

2. Niespójne przedziały ufności

CI (przedział ufności) zależy wyłącznie od wielkości próby. To sprawia, że ​​potencjał zatrzymania jest nieistotny.

3. Szacunkowe wartości CI

Przedziały ufności nie są rozkładem prawdopodobieństwa, a ich wartości dla parametru są jedynie wartościami szacunkowymi, a nie rzeczywistymi.

Powyższe trzy powody zrodziły podejście bayesowskie, które stosuje prawdopodobieństwa do problemów statystycznych.

Narodziny statystyki bayesowskiej

Wielebny Thomas Bayes po raz pierwszy zaproponował bayesowskie podejście do statystyki w swoim eseju napisanym w 1763 roku. Podejście to zostało opublikowane przez Richarda Price'a jako strategia odwrotnego prawdopodobieństwa do prognozowania przyszłych wydarzeń w oparciu o przeszłość.

Podejście opiera się na twierdzeniu Bayesa, które wyjaśniono poniżej:

Twierdzenie Bayesa

Aksjomat prawdopodobieństwa Renyiego bada prawdopodobieństwa warunkowe, w których możliwości wystąpienia zdarzenia A i zdarzenia B są zależne lub warunkowe. Podstawowe prawdopodobieństwo warunkowe można zapisać jako:

Prawdopodobieństwo wystąpienia Zdarzenia B zależy od Zdarzenia A.

Powyższe równanie jest podstawą reguły Bayesa, matematycznego wyrażenia twierdzenia Bayesa, które stwierdza:

Tutaj ∩ oznacza przecięcie.

Regułę Bayesa można zapisać jako:

Reguła Bayesa jest podstawą statystyki bayesowskiej, w której dostępne informacje o danym parametrze w modelu statystycznym są porównywane i aktualizowane zebranymi danymi.

Wiedza podstawowa jest reprezentowana jako rozkład a priori, który jest następnie porównywany i badany z zaobserwowanymi lub zebranymi danymi jako funkcja wiarygodności w celu znalezienia rozkładu a posteriori.

Ten rozkład a posteriori służy do przewidywania przyszłych wydarzeń.

Zastosowania podejścia bayesowskiego zależą od następujących parametrów:

1. Definiowanie a priori i modelu danych
2. Wyciąganie odpowiednich wniosków
3. Analiza i usprawnianie modeli

Czym są Bayesowskie Sieci Neuronowe?

Bayesowskie sieci neuronowe (BNN) to sieci tworzone podczas rozszerzania standardowych sieci przy użyciu metodologii statystycznej i zmiany wnioskowania a posteriori w celu śledzenia nadmiernego dopasowania. Ponieważ jest to podejście bayesowskie, istnieje rozkład prawdopodobieństwa związany z parametrami sieci neuronowych.

Służą do rozwiązywania złożonych problemów, w których nie ma swobodnego przepływu danych. Bayesowskie sieci neuronowe pomagają kontrolować nadmierne dopasowanie w dziedzinach takich jak biologia molekularna i diagnostyka medyczna.

Można rozważyć cały rozkład odpowiedzi na pytanie, a nie tylko jedną możliwość przy użyciu bayesowskich sieci neuronowych. Pomagają w określeniu wyboru/porównania modelu i rozwiązaniu problemów związanych z regularyzacją.

Statystyki bayesowskie oferują narzędzia matematyczne do racjonalizacji i aktualizacji subiektywnej wiedzy dotyczącej nowych danych lub dowodów naukowych. W przeciwieństwie do częstego podejścia statystycznego, funkcjonuje w oparciu o założenie, że prawdopodobieństwa zależą od częstotliwości zdarzeń powtarzających się w tych samych warunkach.

Krótko mówiąc, technika bayesowska jest rozszerzeniem założeń i opinii jednostki. Kluczowym aspektem modelu bayesowskiego, który czyni go bardziej efektywnym, jest zrozumienie, że jednostki różnią się w opiniach w zależności od rodzaju otrzymywanych informacji.

Jednak w miarę pojawiania się nowych dowodów i danych osoby mają punkt zbieżności, wnioskowanie bayesowskie . Ta racjonalna aktualizacja jest szczególną cechą statystyki bayesowskiej, która czyni ją bardziej efektywną w przypadku problemów analitycznych.

Tutaj prawdopodobieństwo 0 jest stosowane, gdy nie ma nadziei na wystąpienie zdarzenia, a prawdopodobieństwo 1 jest stosowane, gdy jest pewne, że zdarzenie nastąpi. Prawdopodobieństwo od 0 do 1 daje miejsce na inne potencjalne wyniki.

Reguła Bayesa jest teraz stosowana w celu uzyskania wnioskowania bayesowskiego w celu uzyskania lepszego wnioskowania z modelu.

Jak zastosować regułę Bayesa do uzyskania wnioskowania bayesowskiego?

Rozważ równanie:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) oznacza wcześniejszy rozkład,

P(θ|D) oznacza późniejsze przekonanie,

P(D) reprezentuje dowód,

P(D|θ) wskazuje na prawdopodobieństwo.

Głównym celem wnioskowania bayesowskiego jest zaoferowanie racjonalnej i matematycznie dokładnej metody łączenia przekonań z dowodami w celu uzyskania zaktualizowanych przekonań a posteriori. Późniejsze przekonania mogą być używane jako wcześniejsze przekonania, gdy generowane są nowe dane. Zatem wnioskowanie bayesowskie pomaga w ciągłym aktualizowaniu przekonań za pomocą reguły Bayesa.

Biorąc pod uwagę ten sam przykład rzucania monetą, model bayesowski aktualizuje procedurę od wcześniejszych do wcześniejszych przekonań o nowe rzuty monetą. Metoda Bayesowska daje następujące prawdopodobieństwa.

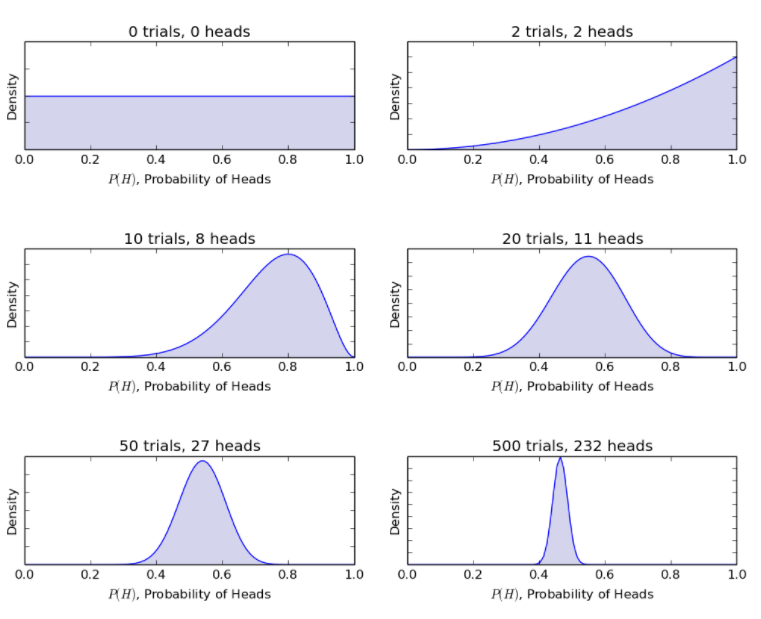
Źródło

W ten sposób model bayesowski pozwala na racjonalizację niepewnego scenariusza z ograniczonymi informacjami do bardziej zdefiniowanego scenariusza z dużą ilością danych.

Znaczące różnice między modelem bayesowskim a modelem częstym

Częste statystyki

Statystyki bayesowskie

Cel jest traktowany jako oszacowanie punktowe, a CI

Cel jest uważany za rozkład tylny

Procedura zaczyna się od obserwacji

Proces rozpoczyna się od wcześniejszej dystrybucji

Za każdym razem, gdy dokonywane są nowe obserwacje, podejście częstościowe ponownie oblicza istniejący model.

Za każdym razem, gdy dokonywane są nowe obserwacje, rozkład a posteriori (ideologia/hipoteza) jest aktualizowany

Przykłady: Estymacja średniej, test t i ANOVA.

Przykłady: Oszacowanie tylnego rozkładu średniej i nakładania się przedziałów o wysokiej gęstości.

Zalety statystyki bayesowskiej

• Zapewnia organiczny i prosty sposób na połączenie wcześniej przyjętych informacji z solidnymi ramami i dowodami naukowymi. Przeszłe informacje o parametrze można wykorzystać do utworzenia wcześniejszego rozkładu do przyszłego badania. Wnioski są zgodne z twierdzeniem Bayesa.
• Wnioski z modelu bayesowskiego są logicznymi i matematycznie dokładnymi, a nie prymitywnymi założeniami. Dokładność pozostaje stała niezależnie od wielkości próbki.
• Statystyka bayesowska opiera się na zasadzie prawdopodobieństwa. Gdy dwie różne próbki mają wspólną funkcję wiarygodności dla przekonania θ, wszystkie wnioski dotyczące przekonania powinny być podobne. Klasyczne techniki statystyczne nie są zgodne z zasadą prawdopodobieństwa.
• Rozwiązania z analizy bayesowskiej można łatwo zinterpretować.
• Oferuje sprzyjającą platformę dla różnych modeli, takich jak modele hierarchiczne i problemy z niekompletnymi danymi. Obliczenia wszystkich modeli parametrycznych można śledzić wirtualnie za pomocą innych technik numerycznych.

Pomyślne zastosowania modeli bayesowskich w historii

Metody bayesowskie miały wiele udanych zastosowań podczas II wojny światowej. Kilka z nich wymieniono poniżej:

• Rosyjski statystyk Andriej Kołmogorow z powodzeniem zastosował metody bayesowskie do poprawy skuteczności rosyjskiej artylerii.
• Modele bayesowskie zostały użyte do złamania kodów niemieckich łodzi podwodnych.
• Urodzony we Francji amerykański matematyk Bernard Koopman pomógł sojusznikom określić położenie niemieckich łodzi podwodnych za pomocą modeli bayesowskich, aby przechwycić transmisje radiowe.

Jeśli chcesz dowiedzieć się więcej o statystykach bayesowskich, zapoznaj się z Zaawansowaną certyfikacją w zakresie uczenia maszynowego i chmury upGrad, aby zrozumieć podstawowe koncepcje w rzeczywistych projektach branżowych i studiach przypadków. 12-miesięczny kurs jest oferowany przez IIT Madras i wspiera naukę we własnym tempie.

Skontaktuj się z nami, aby uzyskać więcej informacji.