Przykład sieci bayesowskiej [z reprezentacją graficzną]

Wstęp

W statystyce modele probabilistyczne są używane do definiowania relacji między zmiennymi i mogą być używane do obliczania prawdopodobieństw każdej zmiennej. W wielu problemach występuje duża liczba zmiennych. W takich przypadkach modele w pełni warunkowe wymagają ogromnej ilości danych, aby objąć każdy przypadek funkcji prawdopodobieństwa, których obliczenie w czasie rzeczywistym może być niewykonalne. Podjęto kilka prób uproszczenia obliczeń prawdopodobieństwa warunkowego, takich jak naiwne Bayesa, ale nadal nie okazuje się to skuteczne, ponieważ drastycznie ogranicza kilka zmiennych.

Jedynym sposobem jest opracowanie modelu, który może zachować warunkowe zależności między zmiennymi losowymi i warunkową niezależność w innych przypadkach. To prowadzi nas do koncepcji sieci bayesowskich. Te sieci bayesowskie pomagają nam skutecznie zwizualizować model probabilistyczny dla każdej domeny i zbadać związek między zmiennymi losowymi w postaci przyjaznego dla użytkownika wykresu.

Ucz się kursu ML z najlepszych światowych uniwersytetów. Zdobywaj programy Masters, Executive PGP lub Advanced Certificate Programy, aby przyspieszyć swoją karierę.

Czym są sieci bayesowskie?

Z definicji sieci bayesowskie są rodzajem probabilistycznego modelu graficznego, który wykorzystuje wnioski bayesowskie do obliczeń prawdopodobieństwa. Reprezentuje zbiór zmiennych i jego prawdopodobieństw warunkowych za pomocą ukierunkowanego grafu acyklicznego (DAG). Nadają się przede wszystkim do rozważenia zdarzenia, które miało miejsce i przewidywania prawdopodobieństwa, że ​​którakolwiek z kilku możliwych znanych przyczyn jest czynnikiem sprawczym.

Źródło

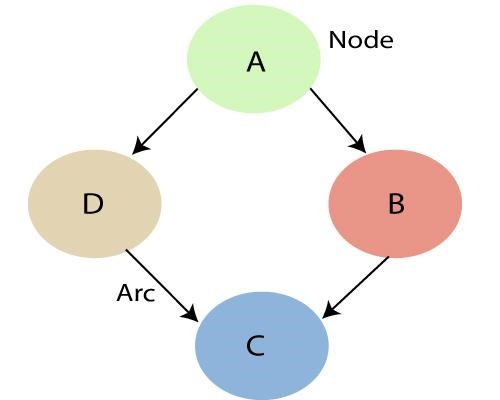
Jak wspomniano powyżej, korzystając z zależności określonych przez sieć bayesowską, możemy otrzymać wspólny rozkład prawdopodobieństwa (JPF) z prawdopodobieństwami warunkowymi. Każdy węzeł na wykresie reprezentuje zmienną losową, a łuk (lub strzałka skierowana) reprezentuje relację między węzłami. Mogą mieć charakter ciągły lub dyskretny.

Na powyższym diagramie A, B, C i D to 4 zmienne losowe reprezentowane przez węzły podane w sieci grafu. Do węzła B, A jest jego węzłem nadrzędnym, a C jest jego węzłem podrzędnym. Węzeł C jest niezależny od węzła A.

Zanim przejdziemy do implementacji sieci bayesowskiej, należy zrozumieć kilka podstaw prawdopodobieństwa.

Lokalna posiadłość Markowa

Sieci Bayesowskie spełniają własność znaną jako Lokalna Własność Markowa. Stwierdza, że ​​węzeł jest warunkowo niezależny od swoich niepotomnych, biorąc pod uwagę jego rodziców. W powyższym przykładzie P(D|A, B) jest równe P(D|A), ponieważ D jest niezależne od swojego niepotomnego, B. Ta właściwość pomaga nam w uproszczeniu Wspólnego Rozkładu. Lokalna właściwość Markowa prowadzi nas do koncepcji losowego pola Markowa, które jest losowym polem wokół zmiennej, o której mówi się, że podąża za właściwościami Markowa.

Warunkowe prawdopodobieństwo

W matematyce prawdopodobieństwo warunkowe zdarzenia A jest prawdopodobieństwem wystąpienia zdarzenia A, biorąc pod uwagę, że inne zdarzenie B już miało miejsce. Mówiąc prościej, p(A | B) jest prawdopodobieństwem wystąpienia zdarzenia A, przy założeniu, że zdarzenie B ma miejsce. Istnieją jednak dwa rodzaje możliwości zdarzeń między A i B. Mogą to być zdarzenia zależne lub zdarzenia niezależne. W zależności od ich typu istnieją dwa różne sposoby obliczania prawdopodobieństwa warunkowego.

• Biorąc pod uwagę, że A i B są zdarzeniami zależnymi, prawdopodobieństwo warunkowe oblicza się jako P (A| B) = P (A i B) / P (B)
• Jeżeli A i B są zdarzeniami niezależnymi, to wyrażenie na prawdopodobieństwo warunkowe jest podane przez: P(A| B) = P (A)

Wspólny rozkład prawdopodobieństwa

Zanim przejdziemy do przykładu sieci bayesowskich, zrozummy pojęcie wspólnego rozkładu prawdopodobieństwa. Rozważ 3 zmienne a1, a2 i a3. Z definicji prawdopodobieństwa wszystkich różnych możliwych kombinacji a1, a2 i a3 nazywane są jego łącznym rozkładem prawdopodobieństwa.

Jeśli P[a1,a2, a3,….., an] jest JPD następujących zmiennych od a1 do an, to istnieje kilka sposobów obliczenia wspólnego rozkładu prawdopodobieństwa jako kombinacji różnych terminów, takich jak:

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., an]….P[an-1|an] * P[an]

Uogólniając powyższe równanie, możemy zapisać wspólny rozkład prawdopodobieństwa jako,

P(X i |X i-1 ,………, X n ) = P(X i | Rodzice(X i ))

Przykład sieci bayesowskich

Przyjrzyjmy się teraz mechanizmowi sieci bayesowskich i ich zaletom na prostym przykładzie. W tym przykładzie wyobraźmy sobie, że otrzymujemy zadanie modelowania ocen ucznia ( m ) z egzaminu, który właśnie zdał. Z podanego poniżej wykresu sieci bayesowskiej widzimy, że oceny zależą od dwóch innych zmiennych. Oni są,

• Poziom egzaminu ( e ) — ta zmienna dyskretna oznacza poziom trudności egzaminu i ma dwie wartości (0 dla łatwego i 1 dla trudnego)
• Poziom IQ ( i ) – reprezentuje poziom ilorazu inteligencji ucznia i ma również charakter dyskretny i ma dwie wartości (0 dla niskiego i 1 dla wysokiego)

Dodatkowo poziom IQ ucznia prowadzi nas również do innej zmiennej, którą jest Wynik Umiejętności ucznia ( ów ). Teraz, z ocenami, które uzyskał student, może zapewnić sobie przyjęcie na konkretną uczelnię. Poniżej podano również rozkład prawdopodobieństwa przyjęcia ( a ) na uniwersytet.

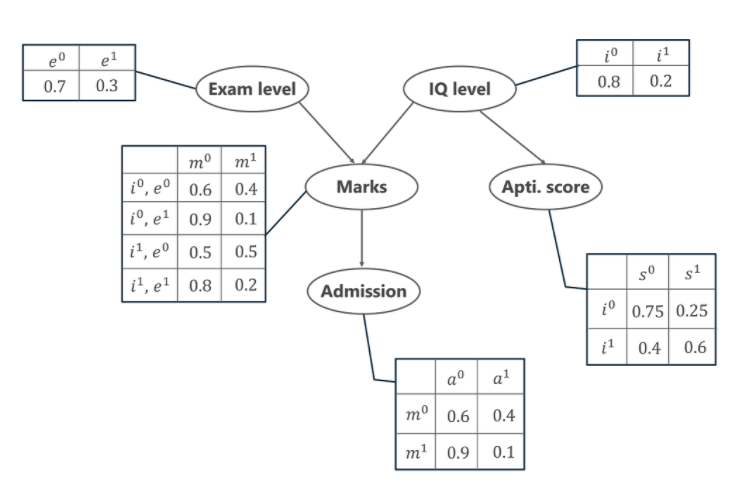
Na powyższym wykresie widzimy kilka tabel reprezentujących wartości rozkładu prawdopodobieństwa danych 5 zmiennych. Tabele te nazywane są tabelą prawdopodobieństw warunkowych lub CPT. Poniżej podano kilka właściwości CPT:

• Suma wartości CPT w każdym wierszu musi być równa 1, ponieważ wszystkie możliwe przypadki dla danej zmiennej są wyczerpujące (reprezentują wszystkie możliwości).
• Jeżeli zmienna o charakterze boolowskim ma k rodziców logicznych, to w CPT ma ona wartości prawdopodobieństwa 2K.

Wracając do naszego problemu, najpierw wypiszmy wszystkie możliwe zdarzenia, które mają miejsce w powyższej tabeli.

1. Poziom egzaminu (e)
2. Poziom IQ (i)
3. Wynik (s) uzdolnień
4. Znaki (m)
5. Wstęp (a)

Te pięć zmiennych jest reprezentowanych w postaci ukierunkowanego wykresu acyklicznego (DAG) w formacie sieci bayesowskiej z ich tabelami prawdopodobieństwa warunkowego. Teraz, aby obliczyć wspólny rozkład prawdopodobieństwa 5 zmiennych, wzór jest podany przez:

P[a, m, i, e, s]= P(a | m). P(m | i, e) . Liczba Pi) . P(e) . P(s | i)

Z powyższego wzoru,

• P(a | m) oznacza warunkowe prawdopodobieństwo przyjęcia studenta na studia na podstawie ocen z egzaminu.
• P(m | i, e) reprezentuje oceny, które uczeń uzyska na podstawie swojego poziomu IQ i trudności poziomu egzaminu.
• P(i) i P(e) reprezentują prawdopodobieństwo poziomu IQ i poziomu egzaminu.
• P(s | i) to warunkowe prawdopodobieństwo Wyniku Umiejętności ucznia, biorąc pod uwagę jego poziom IQ.

Obliczając następujące prawdopodobieństwa, możemy znaleźć łączny rozkład prawdopodobieństwa całej sieci bayesowskiej.

Obliczanie wspólnego rozkładu prawdopodobieństwa

Obliczmy teraz JPD dla dwóch przypadków.

Przypadek 1: Oblicz prawdopodobieństwo, że pomimo trudnego poziomu egzaminu, studentowi o niskim poziomie IQ i niskim Aptitude Score uda się zdać egzamin i zapewnić sobie przyjęcie na uczelnię.

Z powyższego zadania tekstowego, wspólny rozkład prawdopodobieństwa można zapisać jak poniżej,

P[a=1, m=1, i=0, e=1, s=0]

Z powyższych tabel Warunkowego Prawdopodobieństwa wartości dla danych warunków wprowadzane są do wzoru i obliczane jak poniżej.

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) . P(m=1 | i=0, e=1) . P(i=0) . P(e=1) . P(s=0 | i=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0,0018

Przypadek 2: W innym przypadku oblicz prawdopodobieństwo, że uczeń ma wysoki poziom IQ i Aptitude Score, egzamin jest łatwy, ale nie jest zdany i nie gwarantuje przyjęcia na uniwersytet.

Wzór na JPD jest podany przez

P[a=0, m=0, i=1, e=0, s=1]

Zatem,

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) . P(m=0 | i=1, e=0) . P(i=1) . P(e=0) . P(s=1 | i=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0,0252

Dlatego w ten sposób możemy wykorzystać tabele sieci bayesowskich i prawdopodobieństwa do obliczenia prawdopodobieństwa różnych możliwych zdarzeń, które mogą wystąpić.

Przeczytaj także: Pomysły i tematy projektów uczenia maszynowego

Wniosek

Istnieją niezliczone zastosowania sieci Bayesian w filtrowaniu spamu, wyszukiwaniu semantycznym, pobieraniu informacji i wielu innych. Na przykład z danym objawem możemy przewidzieć prawdopodobieństwo wystąpienia choroby z kilkoma innymi czynnikami przyczyniającymi się do choroby. Dlatego w niniejszym artykule przedstawiono koncepcję sieci bayesowskiej wraz z jej implementacją na przykładzie z życia wziętego.

Jeśli chcesz opanować uczenie maszynowe i sztuczną inteligencję, zwiększ swoją karierę dzięki zaawansowanemu kursowi uczenia maszynowego i sztucznej inteligencji z IIIT-B i Liverpool John Moores University.