Twierdzenie Bayesa wyjaśnione na przykładzie – kompletny przewodnik

Wstęp

Co to jest twierdzenie Bayesa?

Twierdzenie Bayesa służy do obliczania prawdopodobieństwa warunkowego, gdy intuicja często zawodzi. Chociaż jest szeroko stosowane w prawdopodobieństwie, twierdzenie to jest również stosowane w dziedzinie uczenia maszynowego. Jego zastosowanie w uczeniu maszynowym obejmuje dopasowanie modelu do szkoleniowego zestawu danych i opracowanie modeli klasyfikacji.

Co to jest prawdopodobieństwo warunkowe?

Prawdopodobieństwo warunkowe jest zwykle definiowane jako prawdopodobieństwo jednego zdarzenia, biorąc pod uwagę wystąpienie innego zdarzenia.

• Jeżeli A i B są dwoma zdarzeniami, to prawdopodobieństwo warunkowe me oznacza się jako P(A przy danym B) lub P(A|B).
• Prawdopodobieństwo warunkowe można obliczyć z prawdopodobieństwa łącznego (A | B) = P(A, B) / P(B)

• Prawdopodobieństwo warunkowe nie jest symetryczne; Na przykład P(A | B) != P(B | A)

Inne sposoby obliczania prawdopodobieństwa warunkowego obejmują wykorzystanie drugiego prawdopodobieństwa warunkowego, tj.

P(A|B) = P(B|A) * P(A) / P(B)

Rewers jest również używany

P(B|A) = P(A|B) * P(B) / P(A)

Ten sposób obliczania jest przydatny, gdy trudno jest obliczyć wspólne prawdopodobieństwo. W przeciwnym razie, gdy dostępne jest odwrotne prawdopodobieństwo warunkowe, obliczenia przez to stają się łatwe.

To alternatywne obliczanie prawdopodobieństwa warunkowego jest określane jako reguła Bayesa lub twierdzenie Bayesa. Jego nazwa pochodzi od osoby, która jako pierwsza go opisała, „wielebnego Thomasa Bayesa”.

Formuła twierdzenia Bayesa

Twierdzenie Bayesa to sposób obliczania prawdopodobieństwa warunkowego, gdy prawdopodobieństwo łączne nie jest dostępne. Czasami nie można uzyskać bezpośredniego dostępu do mianownika. W takich przypadkach alternatywnym sposobem obliczania jest:

P(B) = P(B|A) * P(A) + P(B|nie A) * P(nie A)

Jest to sformułowanie twierdzenia Bayesa, które pokazuje alternatywne obliczenie P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|nie A) * P(nie A)

Powyższy wzór można opisać za pomocą nawiasów wokół mianownika

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|nie A) * P(nie A))

Ponadto, jeśli mamy P(A), to P(nie A) można obliczyć jako

P(nie A) = 1 – P(A)

Podobnie, jeśli mamy P(not B|not A), to P(B|not A) można obliczyć jako

P(B|nie A) = 1 – P(nie B|nie A)

Twierdzenie Bayesa o prawdopodobieństwie warunkowym

Twierdzenie Bayesa składa się z kilku terminów, których nazwy podano na podstawie kontekstu jego zastosowania w równaniu.

Prawdopodobieństwo a posteriori odnosi się do wyniku P(A|B), a prawdopodobieństwo a priori odnosi się do P(A).

• P(A|B): Prawdopodobieństwo a posteriori.
• P(A): Prawdopodobieństwo pierwszeństwa.

Podobnie, P(B|A) i P(B) są określane jako prawdopodobieństwo i dowód.

• P(B|A): Prawdopodobieństwo.
• P(B): Dowód.

Dlatego twierdzenie Bayesa o prawdopodobieństwie warunkowym można przeformułować jako:

Tylny = Prawdopodobieństwo * Wcześniejszy / Dowód

Jeśli musimy obliczyć prawdopodobieństwo wystąpienia pożaru, biorąc pod uwagę, że jest dym, użyjemy następującego równania:

P(ogień|dym) = P(dym|ogień) * P(ogień) / P(dym)

Gdzie P(Ogień) to Priorytet, P(Dym|Ogień) to Prawdopodobieństwo, a P(Dym) to dowód.

Ilustracja twierdzenia Bayesa

Aby zilustrować użycie twierdzenia Bayesa w zadaniu, opisano przykład twierdzenia Bayesa.

Problem

Obecne są trzy pudełka oznaczone jako A, B i C. Szczegóły pudełek to:

• Pudełko A zawiera 2 czerwone i 3 czarne kule
• Pudełko B zawiera 3 czerwone i 1 czarną kulkę
• A pudełko C zawiera 1 czerwoną kulę i 4 czarne kule

Wszystkie trzy pudełka są identyczne i mają jednakowe prawdopodobieństwo, że zostaną podniesione. Jakie jest zatem prawdopodobieństwo, że czerwona piłka została podniesiona z pola A?

Rozwiązanie

Niech E oznacza zdarzenie, w którym czerwona piłka została podniesiona, a A, B i C oznaczają, że piłka została podniesiona z odpowiednich pól. Dlatego prawdopodobieństwo warunkowe byłoby P(A|E), które należy obliczyć.

Istniejące prawdopodobieństwa P(A) = P(B) = P(C) = 1/3, ponieważ wszystkie pola mają jednakowe prawdopodobieństwo trafienia.

P(E|A) = Liczba czerwonych piłek w polu A / Całkowita liczba piłek w polu A = 2 / 5

Podobnie, P(E|B) = 3/4 i P(E|C) = 1/5

Wtedy dowód P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Dlatego P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Przykład twierdzenia Bayesa

Twierdzenie Bayesa podaje prawdopodobieństwo „zdarzenia” z podaną informacją o „testach”.

• Istnieje różnica między „zdarzeniami” a „testami”. Na przykład istnieje test na chorobę wątroby, który różni się od faktycznej choroby wątroby, tj. zdarzenia.
• Rzadkie zdarzenia mogą mieć wyższy współczynnik fałszywych trafień.

Przykład 1

Jakie jest prawdopodobieństwo choroby wątroby u pacjenta będącego alkoholikiem?

Tutaj „bycie alkoholikiem” jest „testem” (rodzajem papierka lakmusowego) na chorobę wątroby.

• A to zdarzenie, tj. „pacjent ma chorobę wątroby”.

Zgodnie z wcześniejszymi zapisami kliniki, stwierdza się, że 10% pacjentów zgłaszających się do kliniki cierpi na choroby wątroby.

Dlatego P(A)=0,10

• B to papierek lakmusowy, że „Pacjent jest alkoholikiem”.

Wcześniejsze zapisy kliniki wskazywały, że 5% pacjentów wchodzących do kliniki to alkoholicy.

Dlatego P(B)=0,05

• Ponadto 7% pacjentów, u których zdiagnozowano chorobę wątroby, to alkoholicy. To określa B|A: prawdopodobieństwo, że pacjent jest alkoholikiem, biorąc pod uwagę, że ma chorobę wątroby, wynosi 7%.

Zgodnie ze wzorem na twierdzenie Bayesa ,

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Dlatego dla pacjenta będącego alkoholikiem prawdopodobieństwo wystąpienia choroby wątroby wynosi 0,14 (14%).

Przykład 2

• Niebezpieczne pożary są rzadkie (1%)
• Ale dym jest dość powszechny (10%) ze względu na grille,
• A 90% niebezpiecznych pożarów powoduje dym

Jakie jest prawdopodobieństwo niebezpiecznego pożaru, gdy jest dym?

Obliczenie

P(ogień|dym) =P(ogień) P(dym|ogień)/P(dym)

= 1% x 90%/10%

= 9%

Przykład 3

Jaka jest szansa na deszcz w ciągu dnia? Gdzie deszcz oznacza deszcz w ciągu dnia, a chmura oznacza pochmurny poranek.

Szansa na deszcz w przypadku chmury jest zapisana jako P (deszcz|chmura)

P(deszcz|chmura) = P(deszcz) P(chmura|deszcz)/P(chmura)

P (deszcz) to prawdopodobieństwo deszczu = 10%

P(chmura|deszcz) to prawdopodobieństwo zachmurzenia, biorąc pod uwagę, że zdarza się deszcz = 50%

P (chmura) to prawdopodobieństwo chmury = 40%

P(deszcz|chmura) = 0,1 x 0,5/0,4 = 0,125

Dlatego 12,5% szans na deszcz.

Aplikacje

W świecie rzeczywistym istnieje kilka zastosowań twierdzenia Bayesa. Kilka głównych zastosowań twierdzenia to:

1. Hipotezy modelowania

Twierdzenie Bayesa znajduje szerokie zastosowanie w stosowanym uczeniu maszynowym i ustanawia związek między danymi a modelem. Stosowane uczenie maszynowe wykorzystuje proces testowania i analizy różnych hipotez na danym zbiorze danych.

Aby opisać związek między danymi a modelem, twierdzenie Bayesa zapewnia model probabilistyczny.

P(h|D) = P(D|h) * P(h) / P(D)

Gdzie,

P(h|D): Prawdopodobieństwo a posteriori hipotezy

P(h): Prawdopodobieństwo a priori hipotezy.

Wzrost P(D) zmniejsza P(h|D). Odwrotnie, jeśli P(h) i prawdopodobieństwo obserwacji danych danej hipotezy wzrasta, to prawdopodobieństwo P(h|D) wzrasta.

2. Twierdzenie Bayesa do klasyfikacji

Metoda klasyfikacji polega na oznakowaniu danych. Można to zdefiniować jako obliczenie warunkowego prawdopodobieństwa etykiety klasy na podstawie próbki danych.

P(klasa|dane) = (P(dane|klasa) * P(klasa)) / P(dane)

Gdzie P(klasa|dane) jest prawdopodobieństwem klasy przy podanych danych.

Obliczenia można przeprowadzić dla każdej klasy. Danym wejściowym można przypisać klasę o największym prawdopodobieństwie.

Obliczenie prawdopodobieństwa warunkowego nie jest możliwe w warunkach małej liczby przykładów. Dlatego bezpośrednie zastosowanie twierdzenia Bayesa nie jest możliwe. Rozwiązaniem modelu klasyfikacji jest uproszczona kalkulacja.

• Naiwny klasyfikator Bayesa

Twierdzenie Bayesa zakłada, że ​​zmienne wejściowe są zależne od innych zmiennych, które powodują złożoność obliczeń. W związku z tym założenie jest usuwane, a każda zmienna wejściowa jest uważana za zmienną niezależną. W rezultacie model zmienia się z zależnego na niezależny model prawdopodobieństwa warunkowego. Ostatecznie zmniejsza złożoność.

To uproszczenie twierdzenia Bayesa jest określane jako Naive Bayes. Jest szeroko stosowany do klasyfikacji i przewidywania modeli.

• Optymalny klasyfikator Bayesa

Jest to rodzaj modelu probabilistycznego, który obejmuje przewidywanie nowego przykładu na podstawie zestawu danych uczących. Jednym z przykładów Bayes Optimal Classifier jest „Jaka jest najbardziej prawdopodobna klasyfikacja nowej instancji, biorąc pod uwagę dane treningowe?”

Obliczenie warunkowego prawdopodobieństwa nowej instancji na podstawie danych uczących można wykonać za pomocą następującego równania:

P(vj | D) = suma {h w H} P(vj | hi) * P(hi | D)

Gdzie vj jest nową instancją do sklasyfikowania,

H to zbiór hipotez do klasyfikacji instancji,

cześć to dana hipoteza,

P(vj | hi) jest prawdopodobieństwem a posteriori dla vi przy danej hipotezie hi oraz

P(hi | D) jest prawdopodobieństwem a posteriori hipotezy hi dla danych D.

3. Zastosowania twierdzenia Bayesa w uczeniu maszynowym

Najczęstszym zastosowaniem twierdzenia Bayesa w uczeniu maszynowym jest rozwój problemów klasyfikacyjnych. Inne zastosowania, a nie klasyfikacja, obejmują modele optymalizacyjne i casualowe.

• Optymalizacja bayesowska

Zawsze wyzwaniem jest znalezienie danych wejściowych, które skutkują minimalnym lub maksymalnym kosztem danej funkcji celu. Optymalizacja bayesowska opiera się na twierdzeniu Bayesa i stanowi aspekt poszukiwania globalnego problemu optymalizacji. Metoda obejmuje budowę modelu probabilistycznego (funkcja zastępcza), przeszukiwanie funkcji akwizycji oraz wybór próbek kandydatów do oceny rzeczywistej funkcji celu.

W stosowanym uczeniu maszynowym optymalizacja bayesowska służy do dostrajania hiperparametrów dobrze działającego modelu.

• Bayesowskie sieci wierzeń

Relacje między zmiennymi można określić za pomocą modeli probabilistycznych. Wykorzystywane są również do obliczania prawdopodobieństw. W pełni warunkowy model prawdopodobieństwa może nie być w stanie obliczyć prawdopodobieństw ze względu na dużą ilość danych. Naive Bayes uprościł podejście do obliczeń. Istnieje jeszcze inna metoda, w której model tworzony jest w oparciu o znaną zależność warunkową między zmiennymi losowymi i niezależność warunkową w innych przypadkach. Sieć bayesowska przedstawia tę zależność i niezależność poprzez probabilistyczny model grafowy z ukierunkowanymi krawędziami. Znana zależność warunkowa jest wyświetlana jako skierowane krawędzie, a brakujące połączenia reprezentują warunkowe zależności w modelu.

4. Bayesowskie filtrowanie spamu

Filtrowanie spamu to kolejne zastosowanie twierdzenia Bayesa. Obecne są dwa wydarzenia:

• Zdarzenie A: wiadomość jest spamem.
• Test X: Wiadomość zawiera określone słowa (X)

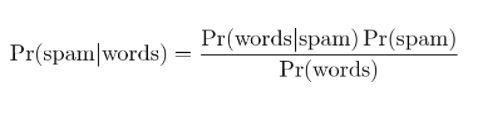
Dzięki zastosowaniu twierdzenia Bayesa można przewidzieć, czy wiadomość jest spamem, biorąc pod uwagę „wyniki testu”. Analiza słów w wiadomości może obliczyć prawdopodobieństwo, że jest to spam. Trenując filtry z powtarzającymi się wiadomościami, aktualizuje fakt, że prawdopodobieństwo posiadania określonych słów w wiadomości będzie spamem.

Zastosowanie twierdzenia Bayesa na przykładzie

Producent katalizatora produkuje urządzenie do badania defektów w pewnym elektrokatalizatorze (EC). Producent katalizatora twierdzi, że test jest wiarygodny w 97%, jeśli EC jest wadliwy i w 99%, gdy jest bezbłędny. Jednak można oczekiwać, że 4% wspomnianego WE będzie wadliwe w momencie dostawy. W celu ustalenia prawdziwej niezawodności urządzenia stosowana jest reguła Bayesa. Podstawowe zestawy wydarzeń to

Odp .: WE jest wadliwa; A': WE jest bez zarzutu; B: WE jest testowany pod kątem wadliwości; B': EC jest testowane pod kątem bezbłędności.

Prawdopodobieństwa byłyby:

B/A: EC jest (wiadomo, że) wadliwe i przetestowane wadliwe, P(B/A) = 0,97,

B'/A: EC jest (wiadomo, że) wadliwe, ale przetestowane bezbłędnie, P(B'/A)=1-P(B/A)=0,03,

B/A': EC jest (wiadomo, że jest) wadliwe, ale testowane wadliwe, P(B/A') = 1- P(B'/A')=0,01

B'/A: = EC jest (wiadomo, że) bez skazy i przetestowane bez skazy P(B'/A') = 0,99

Prawdopodobieństwa obliczone przez twierdzenie Bayesa to:

Prawdopodobieństwo obliczeń pokazuje, że istnieje duże prawdopodobieństwo odrzucenia bezbłędnych EC (około 20%) i niskie prawdopodobieństwo zidentyfikowania wadliwych EC (około 80%).

Wniosek

Jedną z najbardziej uderzających cech twierdzenia Bayesa jest to, że z kilku współczynników prawdopodobieństwa można uzyskać ogromną ilość informacji. Za pomocą metod prawdopodobieństwa prawdopodobieństwo wcześniejszego zdarzenia może zostać przekształcone w prawdopodobieństwo a posteriori. Podejścia twierdzenia Bayesa można zastosować w obszarach statystyki, epistemologii i logiki indukcyjnej.

Jeśli chcesz dowiedzieć się więcej o twierdzeniu Bayesa, sztucznej inteligencji i uczeniu maszynowym, zapoznaj się z programem Executive PG IIIT-B i upGrad w uczeniu maszynowym i sztucznej inteligencji, który jest przeznaczony dla pracujących profesjonalistów i oferuje ponad 450 godzin rygorystycznych szkoleń, ponad 30 przypadków studia i zadania, status absolwentów IIIT-B, ponad 5 praktycznych projektów zwieńczenia i pomoc w pracy z najlepszymi firmami.