베이지안 사고 란 무엇입니까? 소개 및 정리

1700년대 영국의 통계학자이자 철학자인 Thomas Bayes가 제시한 통계적 정리는 전 세계의 과학자와 분석가에게 계속해서 지침이 되고 있습니다. 오늘날 베이지안 사고는 의학, 과학, 기술 및 기타 여러 분야에 적용되며 계속해서 우리의 세계관과 그에 따른 행동에 강력하게 영향을 미치고 있습니다.

Thomas Bayes의 아이디어는 놀라울 정도로 간단했습니다. Bayes에 따르면 가설이 참일 확률은 두 가지 조건, 즉 우리가 이미 알고 있는 것(사전 지식)을 기반으로 한 가설이 얼마나 합리적인지와 새로운 증거에 얼마나 잘 부합하는지에 달려 있습니다. 따라서 베이지안 사고는 전자가 결론으로 ​​점프하기 전에 사전 지식을 포함한다는 점에서 전통적인 가설 테스트와 다릅니다.

예비 소개를 염두에 두고 베이지안 통계에 대해 좀 더 자세히 살펴보겠습니다.

베이지안 통계

간단히 말해서, 베이지안 통계는 새로운 데이터의 증거에 비추어 사전 신념을 업데이트하기 위해 통계 문제에 확률을 적용합니다. 확률은 특정 사건에 대한 믿음의 정도를 나타냅니다.

믿음의 정도는 개인적인 가정이나 이전 실험의 결과를 기반으로 한 사건에 대한 사전 지식을 기반으로 할 수 있습니다. 베이지안 통계는 베이지안 정리를 사용하여 확률을 계산합니다. Bayes의 정리는 차례로 사건과 관련된 새로운 증거 및 사전 정보를 기반으로 사건의 조건부 확률을 설명합니다.

이를 염두에 두고 Bayes의 정리를 깊이 이해하기 전에 조건부 확률의 기본 개념을 살펴보겠습니다.

조건부 확률

조건부 확률은 이전 이벤트 또는 결과의 발생을 기반으로 하는 이벤트 또는 결과의 가능성으로 정의할 수 있습니다. 이는 이전 이벤트의 확률에 후속 또는 조건부 이벤트의 확률을 곱하여 계산됩니다.

개념을 더 잘 이해하기 위해 예제를 살펴보겠습니다 .

• 사건 A는 나들이를 계획하는 가족이 소풍을 가는 것이다. 가족이 소풍을 갈 확률은 80%입니다.
• 사건 B는 가족들이 소풍을 가는 날 비가 온다는 것이다. 일기예보에 따르면 피크닉 당일 강수확률은 60%입니다.
• 따라서 가족이 소풍을 가고 비가 올 확률(P)은 다음과 같이 계산됩니다.

P(피크닉 및 비) = P(비 | 피크닉) P(피크닉) = (0.60) * (0.80) = 0.48

위의 예에서 조건부 확률은 두 사건 A와 B가 서로 관계가 있는지, 즉 가족이 소풍에 가고 같은 날 비가 올 확률을 봅니다.

따라서 조건부 확률은 다른 이벤트 또는 이벤트가 발생했는지 여부 또는 다른 조건이 존재하는지 여부에 관계없이 이벤트가 발생할 가능성을 의미하기 때문에 무조건 확률과 다릅니다.

조건부 확률 공식

조건부 확률 공식은 확률 곱셈 규칙에서 가져옵니다.

P(A 및 B) 또는 P(AUB) = P( B 주어진 A) 또는 P(B | A) * P(A)

위의 방정식에서 P(A 및 B)는 결합 확률로 둘 이상의 이벤트가 동시에 발생할 가능성을 나타냅니다. P(A,B)로도 표기합니다.

곱셈 규칙에서 조건부 확률 방정식을 추론하는 방법은 다음과 같습니다.

1단계: 곱셈 규칙을 적습니다.

P(A 및 B) = P(B | A) * P(A)

2단계: 방정식의 양변을 P(A)로 나눕니다.

P(A 및 B) / P(A) = P(B | A) * P(A) / P(A)

3단계: 방정식의 오른쪽에 있는 P(A)를 취소합니다.

P(A 및 B) / P(A) = P(B | A)

4단계: 방정식을 다시 작성합니다.

P(A 및 B) = P(B | A) / P(A)

따라서 조건부 확률 공식은 다음과 같습니다.

P(A 및 B) = P(B | A) / P(A)

베이즈의 정리

Bayes' Theorem을 사용하여 새롭고 적절한 증거를 기반으로 우리의 신념과 신념을 업데이트할 수 있습니다. 예를 들어, 특정 사람이 암에 걸릴 확률을 알아내려고 할 때 일반적으로 암에 걸린 인구의 백분율로 가정합니다. 그러나 문제의 사람이 일반 흡연자라는 추가 증거를 제시하면 개인이 흡연자인 경우 암에 걸릴 확률이 더 높기 때문에 우리의 인식(및 그에 따른 확률)을 업데이트할 수 있습니다. 따라서 우리는 사전 지식과 추가 증거를 모두 활용하여 추정치를 개선합니다.

베이즈 정리 공식

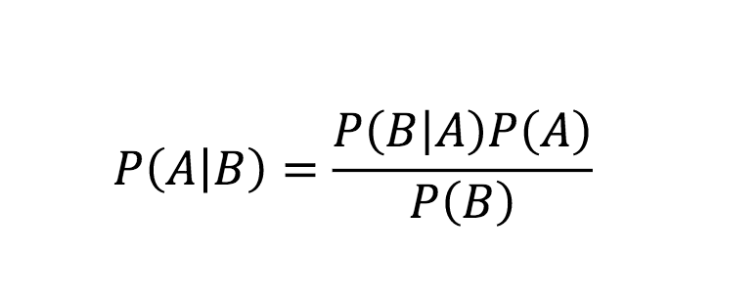
원천

위의 방정식은 Bayes의 법칙입니다. 이제 Bayes' Theorem 방정식의 단계적 유도를 살펴보겠습니다.

1단계: 두 사건 A와 B를 고려합니다. A는 확률을 계산하려는 사건이고 B는 A와 관련된 추가 증거입니다.

2단계: 결합 확률과 사건 A와 B의 조건부 확률 사이의 관계를 기록합니다.

P(A,B) = P(A | B) * P(B) = P(B,A) = P(B | A) * P(A)

3단계: 두 개의 조건부 확률 항을 서로 동일하게 설정합니다.

P(A | B) * P(B) = P(B | A) * P(A)

4단계: 방정식의 양변을 P(B)로 나눕니다.

P(A | B) * P(B) / P(B) = P(B | A) * P(A) / P(B)

5단계: 방정식의 왼쪽에서 P(B)를 취소합니다.

P(A | B) = P(B | A) * P(A) / P(B)

따라서 다음과 같이 Bayes' Theorem의 공식을 얻습니다.

P(A | B) = P(B | A) * P(A) / P(B)

베이즈 정리 방정식의 용어 이해하기

P(A | B) = P(B | A) * P(A) / P(B)

• P(A | B) 를 사후 확률 또는 추정하려는 확률 이라고 합니다 . 앞의 예에 기초하여 사후 확률은 그 사람이 정기적인 흡연자인 경우 암에 걸릴 확률입니다.
• P(B | A) 는 우도 라고 하며 , 초기 가설이 주어졌을 때 추가 증거를 발견할 확률을 나타냅니다. 위의 예에서 가능성은 사람이 암에 걸렸을 때 흡연자가 될 확률입니다.
• P(A) 는 사전 확률 또는 추가 증거나 정보가 없는 가설의 확률입니다. 위의 예에서 사전 확률은 암에 걸릴 확률입니다.
• P(B) 는 증거를 관찰할 수 있는 한계 가능성 또는 총 확률입니다. 위의 예와 관련하여 한계 가능성은 흡연자가 될 확률입니다.

베이즈 정리를 이해하는 간단한 예

이전 예에서 몇 가지 가상 숫자를 사용하여 Bayes' Theorem을 적용한 효과를 볼 수 있습니다.

암에 걸릴 확률이 0.06, 즉 6%의 사람들이 암에 걸렸다고 가정합니다. 이제 흡연자가 될 확률이 0.20 또는 20%의 사람들이 흡연자이고 암에 걸린 사람들의 30%가 흡연자라고 가정합니다. 따라서 P(흡연자 | 암) = 0.30입니다.

초기에 암에 걸릴 확률은 단순히 0.06(이전)입니다. 그러나 새로운 증거를 사용하여 P(암 | 흡연자) = P((흡연자 | 암) * P(암)) / P(흡연자) = (0.30*0.06) / (0.20) = 0.09를 계산할 수 있습니다.

세계 최고의 대학에서 온라인으로 데이터 과학 과정 을 배우십시오 . 이그 제 큐 티브 PG 프로그램, 고급 인증 프로그램 또는 석사 프로그램을 획득하여 경력을 빠르게 추적하십시오.

앞으로 나아갈 길: 데이터 과학 또는 기계 학습 분야의 직업을 위한 통계 개념 마스터

upGrad의 고등 교육 기술 학습 플랫폼은 풍부한 과정과 몰입형 학습 경험을 통해 전 세계적으로 500,000명 이상의 실무 전문가에게 영향을 미쳤습니다. 85개 이상의 국가에 걸쳐 40,000명 이상의 학습자 기반이 있는 upGrad의 업계 관련 과정은 선택한 분야에서 경력을 발전시킬 수 있습니다.

데이터 과학의 이학 석사는 통계, 예측 분석, 기계 학습, 빅 데이터 분석, 데이터 시각화 등의 핵심 기술을 제공하는 18개월 과정입니다.

프로그램 하이라이트:

• 리버풀 존 무어 대학에서 석사 학위 및 IIIT 방갈로르에서 최고 경영자 PGP
• 500시간 이상의 콘텐츠, 60개 이상의 사례 연구 및 프로젝트, 20개 이상의 라이브 세션, 14개 이상의 프로그래밍 언어 및 도구
• 업계 네트워킹, 의심 해결 세션 및 학습 지원

기계 학습 및 딥 러닝의 고급 인증 프로그램은 동료 네트워킹 기회, 실습 프로젝트, 업계 멘토십 및 360도 경력 지원이 포함된 엄격한 6개월 과정입니다.

프로그램 하이라이트:

• IIT 방갈로르의 권위 있는 인정
• 240시간 이상의 콘텐츠, 5개 이상의 사례 연구 및 프로젝트, 24개 이상의 라이브 세션, 12개 프로그래밍 언어, 도구 및 라이브러리 적용
• 업계 전문가와 1:8 그룹 코칭 및 1:1 멘토링

결론

베이지안 사고는 우리 대부분이 그것을 인식하지 못함에도 불구하고 인간의 사고, 탐구, 믿음의 여러 영역을 뒷받침합니다. 암 검진 및 지구 온난화 에서 통화 정책 및 위험 평가 및 보험 에 이르기까지 베이지안 사고는 기본입니다. 유명한 영국 수학자 앨런 튜링 (Alan Turing)조차도 제2차 세계 대전 중에 독일의 수수께끼 암호를 해독하기 위해 베이지안 접근 방식을 사용한 것으로 믿어집니다.

upGrad에 가입하고 주요 통계 개념 등에 대한 지식을 더 넓히십시오!