음의 이항 회귀 분석 시작하기: 단계별 가이드
게시 됨: 2022-04-17Negative Binomial Regression 기법은 카운트 변수의 모델링을 수행하는 데 사용됩니다. 방법은 다중 회귀 방법과 거의 유사합니다. 그러나 음이항회귀의 경우 종속변수인 Y가 음의 이항분포를 따른다는 차이점이 있다. 따라서 변수의 값은 0, 1, 2와 같은 음이 아닌 정수가 될 수 있습니다.
이 방법은 평균이 분산과 같다고 가정할 때 완화하는 푸아송 회귀의 확장이기도 합니다. "NB2"로 정의되는 이항 회귀의 기존 모델 중 하나는 푸아송-감마의 혼합 분포를 기반으로 합니다.
Poisson 회귀의 방법은 감마 노이즈의 변수를 추가하여 일반화됩니다. 이 변수는 평균값이 1이고 척도 매개변수가 "v"입니다.
다음은 음의 이항 회귀의 몇 가지 예입니다.
- 학교 관리자는 두 학교의 고등학생의 출석 행동을 연구하기 위해 연구를 수행했습니다. 출석 행동에 영향을 줄 수 있는 요인에는 후배가 결석한 날이 포함될 수 있습니다. 또한 그들이 등록한 프로그램.
- 건강 관련 연구의 연구원은 지난 12개월 동안 얼마나 많은 노인들이 병원을 방문했는지에 대한 연구를 수행했습니다. 연구는 개인의 특성과 노인들이 구입한 건강 플랜을 기반으로 했습니다.
음의 이항 회귀의 예
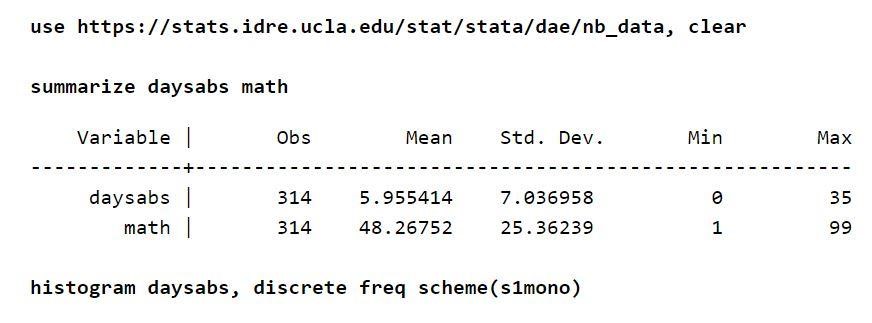
약 314명의 고등학생의 출석표가 있다고 가정합니다. 데이터는 두 개의 도시 학교에서 가져와 nb_data.dta라는 파일에 저장됩니다. 이 예에서 흥미로운 응답 변수는 "daysab"인 부재일입니다. 모든 학생의 수학 점수를 정의하는 "수학"이라는 변수가 하나 있습니다. "prog"라는 또 다른 변수가 있습니다. 이 변수는 학생들이 등록한 프로그램을 나타냅니다.
원천

각 변수에는 약 314개의 관측치가 있습니다. 따라서 변수 간의 분포도 합리적입니다. 또한 결과변수를 고려하면 무조건 평균이 분산보다 낮다.
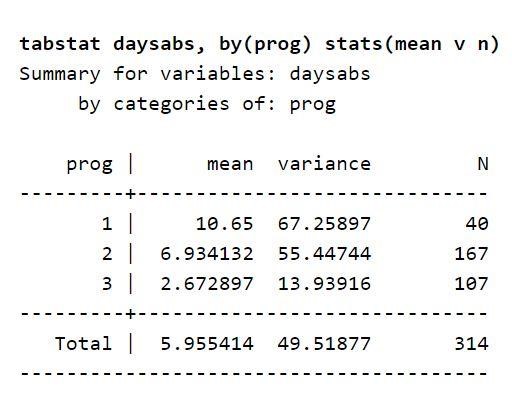
이제 데이터 세트에서 고려되는 변수 설명에 초점을 맞춥니다. 표에는 모든 프로그램 유형에서 학생이 결석한 평균 일수가 나와 있습니다. 이는 변수형 프로그램이 결석일을 예측할 수 있음을 시사한다. 결과 변수를 예측하는 데 사용할 수도 있습니다. 이는 결과 변수의 평균값이 변수 prog에 따라 다르기 때문입니다. 또한 분산 값은 변수 prog의 각 수준에서보다 높습니다. 이러한 값을 분산 및 평균이라고 합니다. 기존 차이점은 과산포가 존재함을 시사하므로 음의 이항 모델을 사용하는 것이 적절할 것입니다.
원천
연구자는 이러한 유형의 연구에 대해 몇 가지 분석 방법을 고려할 수 있습니다. 이러한 방법은 아래에 설명되어 있습니다. 사용자가 회귀 모델을 분석하는 데 사용할 수 있는 몇 가지 분석 방법은 다음과 같습니다.
1. 음의 이항 회귀
Negative Binomial Regression 방법은 데이터가 과분산된 경우에 사용합니다. 이는 조건부 분산 값이 조건부 평균 값보다 높거나 초과한다는 것을 의미합니다. 이 방법은 Poisson 회귀 방법에서 일반화한 것으로 간주됩니다. 이는 두 방법 모두 평균 구조가 동일하기 때문입니다. 그러나 과대산포를 모델링하는 데 사용되는 음의 이항 회귀 분석에는 추가 매개변수가 있습니다. 조건부 분포가 결과 변수에서 과도하게 분산된 경우 신뢰 구간은 열정 회귀보다 좁은 것으로 간주됩니다.
2. 푸아송 회귀
카운트 데이터의 모델링에는 푸아송 회귀 방법이 사용됩니다. 푸아송 회귀에서 개수 변수를 모델링하는 데 많은 확장을 사용할 수 있습니다.
3. OLS 회귀
카운트 변수의 결과는 때때로 로그 변환된 후 OLS 회귀 방법을 통해 분석됩니다. 그러나 때때로 OLS 회귀 방법과 관련된 문제가 있습니다. 이러한 문제는 값 0의 로그를 고려하여 정의되지 않은 값 생성으로 인한 데이터 손실일 수 있습니다. 또한 분산된 데이터를 모델링하지 못하여 생성될 수 있습니다.
4. 제로 팽창 모델
이러한 유형의 모델은 모델의 모든 초과 0을 설명하려고 합니다.
음의 이항 회귀를 사용한 분석
"nbreg" 명령은 음이항 회귀 모델을 추정하는 데 사용됩니다. "prog" 변수 앞에 "i"가 있습니다. "i"의 존재는 변수가 유형 요인, 즉 범주형 변수임을 나타냅니다. 이들은 모델에 지표 변수로 포함되어야 합니다.

- 모델의 출력은 반복 로그로 시작됩니다. Poisson 모델의 피팅을 통해 시작하고, null 모델, 음의 이항 모델이 이어집니다. 이 방법은 최대 가능성의 추정치를 사용하고 최종 로그 값이 변경될 때까지 계속 반복합니다. 로그의 가능성은 모델 비교에 사용됩니다.
- 다음 정보는 헤더 파일에 있습니다.
- 헤더 바로 아래에 Negative Binomial Regression 계수 정보가 있습니다. 계수는 p-값, z-점수와 같은 오류와 함께 모든 변수에 대해 생성됩니다. 또한 모든 계수에 대해 95%의 신뢰 구간이 있습니다. "수학" 변수의 계수는 -0.006으로 통계적으로 유의함을 나타냅니다. 결과는 변수 "수학"에서 한 단위가 증가하면 부재일 수에 대한 예상 로그 수가 0.006 값만큼 감소한다는 것을 의미합니다. 또한 지시변수인 2. prog의 값은 두 그룹(그룹 2 및 참조 그룹) 간의 로그 카운트에서 예상되는 차이입니다.
- 로그 전송 과산포에 대한 매개변수 추정이 완료되고 변환되지 않은 값으로 표시됩니다. 푸아송 모델에서 값은 0입니다.
- 계수 테이블 아래에 비율 테스트 가능성 정보가 있습니다. 모델은 "여백" 명령을 사용하여 더 자세히 이해할 수 있습니다.
Python에서 음이항 회귀 분석을 수행하는 프로세스
회귀 프로세스를 수행하는 데 필요한 패키지는 Python에서 가져와야 합니다. 이러한 패키지는 다음과 같습니다.

- statsmodels.api를 sm으로 가져오기
- matplotlib.pyplot을 plt로 가져오기
- numpy를 np로 가져오기
- patsy import dmatrices에서
- pandas를 pd로 가져오기
음의 이항 회귀 분석에 대한 고려 사항
Negative Binomial Regression 분석 방법을 적용할 때 고려해야 할 몇 가지 사항이 있습니다. 여기에는 다음이 포함됩니다.
- 작은 표본이 있는 경우 음의 이항 회귀 방법은 권장되지 않습니다.
- 때때로 과대산포의 원인이 될 수 있는 초과 0이 존재합니다. 이러한 0은 데이터 생성 추가 프로세스로 인해 생성될 수 있습니다. 이러한 유형의 경우가 발생하면 제로 팽창 모델의 방법을 사용하는 것이 좋습니다.
- 데이터 생성 프로세스에서 0을 고려하지 않는 경우 이러한 경우 0이 잘린 모델의 방법을 사용하는 것이 좋습니다.
- 카운트 데이터와 관련된 노출 변수가 있습니다. 변수는 이벤트가 발생할 수 있는 기회가 있는 시간을 나타냅니다. 이 변수는 Negative Binomial Regression 모델에 통합하는 데 필요합니다. 이것은 exp() 옵션을 통해 수행됩니다.
- 음 이항 회귀 분석 모델에서 결과 변수는 음수 값이 될 수 없습니다. 또한 노출 변수는 값 0을 가질 수 없습니다.
- "glm" 명령은 음이항 회귀 분석 방법을 실행하는 데에도 사용할 수 있습니다. 이것은 로그의 링크와 이항식 계열을 통해 수행할 수 있습니다.
- 잔차를 구하려면 "glm" 명령이 필요합니다. 이것은 Negative Binomial Regression의 모델에 다른 가정이 있는지 확인하기 위한 것입니다.
- 의사 R 제곱의 다양한 측정값이 존재합니다. 그러나 모든 측정값은 OLS 회귀에서 R-제곱이 제공하는 정보와 유사한 정보를 제공합니다.
결론
이 기사에서는 음의 이항 회귀( Negative Binomial Regression ) 주제에 대해 논의했습니다 . 우리는 이것이 다중 회귀 방법과 거의 유사하고 포아송 분포의 일반화된 형태임을 보았습니다. 방법의 여러 응용 프로그램이 있습니다. 이 기술은 Python 프로그래밍 언어나 R을 통해 적용할 수도 있습니다.
노화와 같은 연구에서의 적용을 보여주는 여러 사례 연구도 있습니다. 또한 계수 데이터에 사용할 수 있는 회귀의 고전적 모델은 포아송 회귀, 음의 이항 회귀 및 기하 회귀입니다. 이러한 방법은 선형 모델 계열에 속하며 R 시스템과 같은 거의 모든 통계 패키지에 포함되었습니다.
머신 러닝에 뛰어나고 데이터 분야를 탐색하고 싶다면 upGrad에서 제공하는 머신 러닝 및 AI의 Executive PG Program 과정을 확인할 수 있습니다. 따라서 머신러닝 전문가를 꿈꾸는 실무 전문가라면 오셔서 전문가 밑에서 교육을 받는 경험을 해보세요. 자세한 내용은 당사 웹사이트를 통해 확인할 수 있습니다. 문의 사항이 있는 경우 당사 팀에서 신속하게 도움을 드릴 수 있습니다.