기계 학습을 위한 나이브 베이즈 알고리즘 배우기 [예제 포함]
게시 됨: 2021-02-25목차
소개
수학 및 프로그래밍에서 가장 간단한 솔루션 중 일부는 일반적으로 가장 강력한 솔루션입니다. Naive Bayes Algorithm은 이 문장의 전형적인 예입니다. 기계 학습 분야의 강력하고 빠른 발전과 발전에도 불구하고 이 나이브 베이즈 알고리즘은 여전히 가장 널리 사용되는 효율적인 알고리즘 중 하나로 굳건히 자리잡고 있습니다. 나이브 베이즈 알고리즘은 분류 작업 및 자연어 처리(NLP) 문제를 비롯한 다양한 문제에서 응용 프로그램을 찾습니다.
Bayes Theorem의 수학적 가설은 이 Naive Bayes 알고리즘의 기본 개념으로 사용됩니다. 이 글에서 우리는 베이즈 정리의 기초, 나이브 베이즈 알고리즘과 실시간 예제 문제를 파이썬으로 구현하는 방법에 대해 알아볼 것입니다. 이와 함께 Naive Bayes Algorithm의 장점과 단점을 경쟁 제품과 비교하여 살펴보겠습니다.
확률의 기초
Bayes Theorem과 Naive Bayes Algorithm을 이해하기 시작하기 전에 Probability의 기초에 대한 기존 지식을 정리하겠습니다.
정의에 의해 우리 모두가 알고 있듯이 이벤트 A가 주어지면 해당 이벤트가 발생할 확률은 P(A)로 표시됩니다. 확률에서 두 사건 A와 B는 사건 A의 발생이 사건 B의 발생 확률을 변경하지 않고 그 반대의 경우에도 독립 사건이라고 합니다. 반면에 하나의 발생이 다른 하나의 확률을 변경하면 종속 이벤트라고 합니다.
Conditional Probability 라는 새로운 용어를 소개하겠습니다 . 수학에서 P(A| B)로 주어진 두 사건 A와 B에 대한 조건부 확률은 사건 B가 이미 발생한 경우 사건 A가 발생할 확률로 정의됩니다. 종속 또는 독립 여부에 대한 두 이벤트 A와 B 사이의 관계에 따라 조건부 확률은 두 가지 방식으로 계산됩니다.
- 두 종속 이벤트 A 및 B의 조건부 확률은 P(A| B) = P(A 및 B) / P(B)로 표시됩니다.
- 두 개의 독립적인 사건 A와 B 의 조건부 확률에 대한 표현은 다음과 같습니다. P(A| B) = P(A)
확률과 조건부 확률 뒤에 있는 수학을 알았으니 이제 베이즈 정리로 넘어 갑시다.

베이즈 정리
통계 및 확률 이론에서 베이즈의 규칙이라고도 알려진 베이즈의 정리는 이벤트의 조건부 확률을 결정하는 데 사용됩니다. 즉, Bayes의 정리는 이벤트와 관련될 수 있는 조건에 대한 사전 지식을 기반으로 이벤트의 확률을 설명합니다.
더 쉽게 이해하려면 집값이 매우 높을 확률을 알아야 한다고 생각해보자. 근처에 학교, 의료 상점 및 병원이 있는지 여부와 같은 다른 매개변수에 대해 알면 더 정확하게 평가할 수 있습니다. 이것이 바로 Bayes Theorem이 수행하는 것입니다.
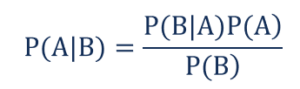
그런,
- P(A|B) – 이벤트 B가 발생했을 때 이벤트 A가 발생할 조건부 확률은 사후 확률 이라고도 합니다.
- P(B|A) – 이벤트 A가 발생했을 때 발생하는 이벤트 B의 조건부 확률은 우도 확률 이라고도 합니다.
- P(A) – 사전 확률이라고도 하는 사건 A가 발생할 확률.
- P(B) – 한계 확률 이라고도 하는 사건 B가 발생할 확률.
'n'개의 독립 변수와 출력인 종속 변수가 부울 값(True 또는 False)인 간단한 기계 학습 문제가 있다고 가정합니다. 독립 속성이 본질적으로 범주형이라고 가정하고 이 예에 대해 2개의 범주를 고려하겠습니다. 따라서 이러한 데이터를 사용하여 우도 확률 P(B|A)의 값을 계산해야 합니다.
따라서 위의 내용을 관찰하면 이 기계 학습 모델을 학습하기 위해 2*(2^ n -1 ) 매개변수 를 계산해야 함을 알 수 있습니다. 마찬가지로 30개의 독립 부울 속성이 있는 경우 계산할 매개변수의 총 수는 30억에 가까우므로 계산 비용이 매우 높습니다.
Bayes Theorem으로 기계 학습 모델을 구축하는 데 있어 이러한 어려움은 Naive Bayes 알고리즘의 탄생과 개발로 이어졌습니다.
나이브 베이즈 알고리즘
실용적이기 위해서는 위에서 언급한 Bayes Theorem의 복잡성을 줄여야 합니다. 이것은 Naive Bayes Algorithm에서 몇 가지 가정을 함으로써 정확하게 달성됩니다. 만들어진 가정은 각 기능이 결과에 독립 적이고 동등한 기여를 한다는 것입니다.
Naive Bayes Algorithm은 지도 학습 알고리즘이며 주로 분류 문제를 해결하는 데 사용되는 Bayes 정리를 기반으로 합니다. 빠른 예측을 위해 기계 학습 모델을 구축하는 가장 간단하고 정확한 분류기 중 하나입니다. 수학적으로는 이벤트의 확률 함수를 사용하여 예측을 수행하므로 확률론적 분류기입니다.
예제 문제
가정 뒤에 있는 논리를 이해하기 위해 더 나은 직관을 얻기 위해 간단한 데이터 세트를 살펴보겠습니다.
| 색깔 | 유형 | 기원 | 훔침? |
| 검은 색 | 의자 가마 | 수입 | 네 |
| 검은 색 | SUV | 수입 | 아니요 |
| 검은 색 | 의자 가마 | 국내의 | 네 |
| 검은 색 | 의자 가마 | 수입 | 아니요 |
| 갈색 | SUV | 국내의 | 네 |
| 갈색 | SUV | 국내의 | 아니요 |
| 갈색 | 의자 가마 | 수입 | 아니요 |
| 갈색 | SUV | 수입 | 네 |
| 갈색 | 의자 가마 | 국내의 | 아니요 |
위에 주어진 데이터 세트에서 우리는 위의 Naive Bayes 알고리즘에 대해 정의한 두 가지 가정의 개념을 도출할 수 있습니다.
- 첫 번째 가정은 모든 기능이 서로 독립적이라는 것입니다. 여기에서 "빨간색" 색상 이 자동차의 유형 및 원산지와 무관 한 것처럼 각 속성이 독립적임을 알 수 있습니다.
- 다음으로, 각 기능에 동일한 중요성을 부여해야 합니다. 마찬가지로, 자동차의 유형과 원산지에 대한 지식만으로는 문제의 결과를 예측하기에 충분하지 않습니다. 따라서 변수 중 어느 것도 관련이 없으며 따라서 모두 결과에 동등하게 기여합니다.
요약하자면 A와 B는 C가 주어졌을 때 조건부 독립입니다. C가 발생한다는 지식이 주어졌을 때 A가 발생했는지 여부에 대한 지식은 B가 발생할 가능성에 대한 정보를 제공하지 않고 B가 발생했는지 여부에 대한 지식은 A가 발생할 가능성. 이러한 가정은 Bayes 알고리즘을 Naive 로 만듭니다. 따라서 이름은 나이브 베이즈 알고리즘입니다.
따라서 위에 주어진 문제에 대해 Bayes Theorem은 다음과 같이 다시 쓸 수 있습니다.
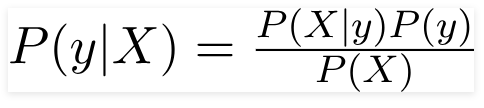
그런,
- 독립 특징 벡터 X = (x 1 , x 2 , x 3 …x n )은 자동차의 색상, 유형 및 원점과 같은 특징을 나타냅니다.
- 출력 변수 y에는 Yes 또는 No의 두 가지 결과만 있습니다.
따라서 위의 값을 대입하여 Naive Bayes Formula를 다음과 같이 얻습니다.
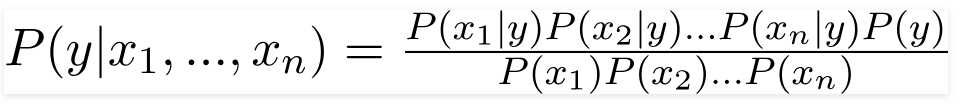
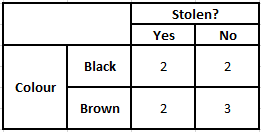
사후 확률 P(y|X)를 계산하려면 출력에 대한 각 속성에 대한 빈도 테이블을 만들어야 합니다. 그런 다음 빈도 테이블을 가능성 테이블로 변환한 후 최종적으로 나이브 베이지안 방정식을 사용하여 각 클래스에 대한 사후 확률을 계산합니다. 사후 확률이 가장 높은 클래스가 예측 결과로 선택됩니다. 다음은 세 가지 예측 변수 모두에 대한 빈도 및 가능성 표입니다.
색상의 빈도 표 색상 가능성 표
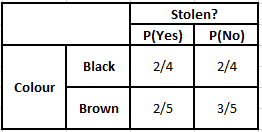
유형의 빈도 테이블 유형의 가능성 테이블
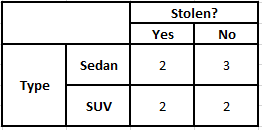
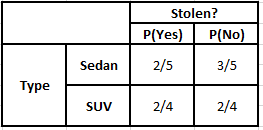

기원의 빈도표 기원의 가능성 표
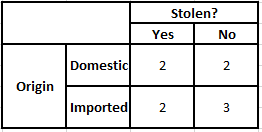
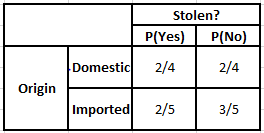
아래 주어진 조건에 대한 사후 확률을 계산해야 하는 경우를 고려하십시오.
| 색깔 | 유형 | 기원 |
| 갈색 | SUV | 수입 |
따라서 위의 주어진 공식에서 다음과 같이 사후 확률을 계산할 수 있습니다.
P(예 | X) = P(브라운 | 예) * P(SUV | 예) * P(수입 | 예) * P(예)
= 2/5 * 2/4 * 2/5 * 1
= 0.08
P(아니요 | X) = P(갈색 | 아니요) * P(SUV | 아니요) * P(수입 | 아니요) * P(아니요)
= 3/5 * 2/4 * 3/5 * 1
= 0.18
위와 같이 계산된 값들로부터 No에 대한 사후확률이 Yes보다 크므로(0.18>0.08), Brown Color, SUV Type of Imported Origin의 차량은 "No"로 분류됨을 유추할 수 있습니다. 따라서 차는 도난당하지 않습니다.
파이썬에서의 구현
이제 Naive Bayes 알고리즘의 이면에 있는 수학을 이해하고 예제를 통해 시각화했으므로 Python 언어로 기계 학습 코드를 살펴보겠습니다.
관련 항목: 나이브 베이즈 분류기
문제 분석
Python을 사용하여 기계 학습에서 Naive Bayes 분류 프로그램을 구현하기 위해 매우 유명한 'Iris Flower Dataset'을 사용할 것입니다. Iris flower 데이터셋 또는 Fisher's Iris 데이터셋은 1998년 영국의 통계학자이자 우생학자이자 생물학자인 Ronald Fisher에 의해 도입된 다변량 데이터셋입니다. 이것은 3개의 클래스에 대한 정보를 포함하는 매우 적은 수의 데이터로 구성된 매우 작고 기본적인 데이터셋입니다. 붓꽃 종에 속하는 꽃은 다음과 같습니다.
- 아이리스 세토사
- 아이리스 버시컬러
- 아이리스 버지니아
150행의 총 데이터 세트에 해당 하는 세 종 의 각 샘플이 50 개 있습니다. 이 데이터 세트에 사용된 4개의 속성(또는) 독립 변수는 다음과 같습니다.
- 꽃받침 길이(cm)
- 꽃받침 너비(cm)
- 꽃잎 길이(cm)
- 꽃잎 너비(cm)
종속변수는 위에 주어진 네 가지 속성에 의해 식별되는 꽃 의 " 종 "입니다.
1단계 – 라이브러리 가져오기
항상 그렇듯이 머신 러닝 모델을 구축하는 기본 단계는 관련 라이브러리를 가져오는 것입니다. 이를 위해 데이터 전처리를 위한 NumPy, Mathplotlib 및 Pandas 라이브러리를 로드합니다.
numpy를 np로 가져오기
matplotlib.pyplot을 plt로 가져오기
pandas를 pd로 가져오기
2단계 – 데이터 세트 로드
Naive Bayes Classifier 훈련에 사용할 홍채 꽃 데이터 세트는 Pandas DataFrame에 로드됩니다. 4개의 독립 변수는 변수 X에 할당되고 최종 출력 종 변수는 y에 할당됩니다.
데이터 세트 = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc[:,:4].values
y = 데이터세트['종'].valuesdataset.head(5)>>
sepal_length sepal_width 꽃잎_length 꽃잎_width 종
5.1 3.5 1.4 0.2 세토사
4.9 3.0 1.4 0.2 세토사
4.7 3.2 1.3 0.2 세토사
4.6 3.1 1.5 0.2 세토사
5.0 3.6 1.4 0.2 세토사
3단계 – 데이터 세트를 훈련 세트와 테스트 세트로 분할
데이터 세트와 변수를 로드한 후 다음 단계는 훈련 프로세스를 거칠 변수를 준비하는 것입니다. 이 단계에서는 X 및 y 변수를 훈련 데이터 세트와 테스트 데이터 세트로 분할해야 합니다. 이를 위해 데이터의 80%를 훈련 목적으로 사용할 훈련 세트에 무작위로 할당하고 데이터의 나머지 20%를 훈련된 나이브 베이즈 분류기가 정확도에 대해 테스트할 테스트 세트로 할당합니다.
sklearn.model_selection import train_test_split에서
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
4단계 – 기능 확장
이것은 이 작은 데이터 세트에 대한 추가 프로세스이지만 더 큰 데이터 세트에서 사용할 수 있도록 추가합니다. 여기에서 훈련 및 테스트 세트의 데이터는 0과 1 사이의 값 범위로 축소됩니다. 이렇게 하면 계산 비용이 줄어듭니다.
sklearn.preprocessing 가져오기 StandardScaler에서
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
5단계 – 훈련 세트에서 나이브 베이즈 분류 모델 훈련
이 단계에서 sklearn 라이브러리에서 Naive Bayes 클래스를 가져옵니다. 이 모델의 경우 가우스 모델을 사용하며 Bernoulli, Categorical 및 Multinomial과 같은 몇 가지 다른 모델이 있습니다. 따라서 X_train 및 y_train은 훈련 목적으로 분류기 변수에 적합합니다.
sklearn.naive_bayes에서 GaussianNB 가져오기
분류기 = GaussianNB()
classifier.fit(X_train, y_train)
6단계 – 테스트 세트 결과 예측 –
훈련된 모델을 사용하여 테스트 세트에 대한 종의 클래스를 예측하고 종 클래스의 실제 값과 비교합니다.
y_pred = classifier.predict(X_test)
df = pd.DataFrame({'실제 값':y_test, '예상 값':y_pred})
DF>>
실제 값 예측 값
세토사 세토사
세토사 세토사
버지니아 버지니아
버시 컬러 버시 컬러
세토사 세토사
세토사 세토사
… … … … …
버지니아 베르시 컬러
버지니아 버지니아
세토사 세토사
세토사 세토사
버시 컬러 버시 컬러
버시 컬러 버시 컬러
위의 비교에서 Virginica 대신 Versicolor를 예측한 잘못된 예측이 하나 있음을 알 수 있습니다.
7단계 – 혼동 매트릭스 및 정확도
분류를 다룰 때 분류기 모델을 평가하는 가장 좋은 방법은 테스트 세트의 정확도와 함께 Confusion Matrix를 인쇄하는 것입니다.
sklearn.metrics에서 혼동_매트릭스 가져오기
cm = sklearn.metrics 가져오기 정확도_점수에서 cm =confusion_matrix(y_test, y_pred)

인쇄("정확도 : ", 정확도_점수(y_test, y_pred))
cm >> 정확도 : 0.9666666666666667
>>배열([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
결론
따라서 이 기사에서는 Naive Bayes 알고리즘의 기본 사항을 살펴보고 손으로 해결한 예제와 함께 분류 이면의 수학을 이해했습니다. 마지막으로 Naive Bayes Classification 알고리즘을 사용하여 인기 있는 데이터 세트를 해결하기 위해 기계 학습 코드를 구현했습니다.
AI, 기계 학습에 대해 자세히 알아보려면 IIIT-B & upGrad의 기계 학습 및 AI PG 디플로마를 확인하십시오. 기계 학습 및 AI는 일하는 전문가를 위해 설계되었으며 450시간 이상의 엄격한 교육, 30개 이상의 사례 연구 및 과제를 제공합니다. IIIT-B 동문 자격, 5개 이상의 실용적인 실습 캡스톤 프로젝트 및 최고의 기업과의 취업 지원.
확률은 기계 학습에서 어떻게 도움이 되나요?
실제 시나리오에서 부분적이거나 불완전한 정보를 기반으로 결정을 내려야 할 수도 있습니다. 확률은 그러한 시스템의 불확실성을 수량화하고 작업에 대한 위험을 관리하는 데 도움이 됩니다. 전통적인 방법은 특정 작업에 대한 결정론적 결과에만 작동하지만 모든 예측 모델에는 항상 일정 범위의 불확실성이 있습니다. 이 불확실성은 데이터의 노이즈와 같은 입력 데이터의 많은 매개변수에서 비롯될 수 있습니다. 또한 확률 정리의 베이지안 보기는 입력 데이터의 패턴 인식에 도움이 될 수 있습니다. 이를 위해 확률은 최대 우도 추정 개념을 사용하므로 관련 결과를 생성하는 데 도움이 됩니다.
Confusion Matrix의 용도는 무엇입니까?
혼동 행렬은 분류 모델의 성능을 해석하는 데 사용되는 2x2 행렬입니다. 이것이 작동하려면 입력 데이터의 실제 값을 알아야 하므로 레이블이 지정되지 않은 데이터에 대해 표현할 수 없습니다. 거짓양성(FP), 참양성(TP), 거짓음성(FN), 참음성(TN)의 수로 구성됩니다. 예측은 훈련 세트와 테스트 세트의 카운트를 사용하여 이러한 클래스로 분류됩니다. 정확도, 정밀도, 재현율 및 특이성과 같은 유용한 매개변수를 시각화하는 데 도움이 됩니다. 비교적 이해하기 쉽고 알고리즘에 대한 명확한 아이디어를 제공합니다.
나이브 베이즈 모델의 다른 유형은 무엇입니까?
모든 유형은 주로 베이즈 정리를 기반으로 합니다. Naive Bayes 모델에는 일반적으로 Gaussian, Bernoulli 및 Multinomial의 세 가지 유형이 있습니다. Gaussian Naive Bayes는 입력 매개변수의 연속 값을 지원하며 입력 데이터의 모든 클래스가 균일하게 분포되어 있다고 가정합니다. Bernoulli의 순진한 Bayes는 데이터 기능이 독립적이고 부울 값으로 표시되는 이벤트 기반 모델입니다. Multinomial Naive Bayes도 이벤트 기반 모델을 기반으로 합니다. 이벤트 발생에 따라 관련 빈도를 나타내는 벡터 형식의 데이터 기능이 있습니다.
