データ構造内のツリー：すべてのデータサイエンティストが知っておくべき8種類のツリー

序章

コンピューティングドメインでは、データ構造はディスク上のデータ配置のパターンを指し、これにより便利なストレージと表示が可能になります。 それらは、2021年に有利なキャリアの選択であると予測されたデータサイエンスの分野に関連しています。今後数年間の予測に基づいて、大規模なディープラーニングモデルと次世代のスマートデバイスがこのセクター。

したがって、データ構造の知識を取得することは、技術の進歩の中で適切なキャリアを見つけるために不可欠です。 2021年のデータサイエンス業界の予測によると、米国とインドは、250,000以上の企業内で約50000人のデータサイエンティストと300,000人のデータアナリストを雇用します。 [1]

データ構造は、情報の割り当て、管理、および取得の経路を設計するために適用されます。 データ構造は、処理されるデータ全体の効率を向上させるために特に必要です。 彼らは、情報交換を効果的に促進するためにデータをグループ化および編成することによってデータを管理します。

データ構造のツリー

「ツリー」はADT（抽象データ型）の一種であり、データ割り当ての階層パターンに従います。 基本的に、ツリーはエッジを介して接続された複数のノードのコレクションです。 これらの「ツリー」は、ツリーに似たデータ構造設計を形成します。「ルート」ノードは「親」ノードにつながり、最終的には「子」ノードにつながります。 接続は「エッジ」と呼ばれる線で行われます。

「リーフ」ノードはエンドポイントであり、それらから発信される子ノードはありません。 データ構造内のツリーは、その配置が非線形であるため、重要な役割を果たします。 これにより、検索中の応答時間が短縮され、設計段階全体での利便性が向上します。

データ構造内のツリーの種類

データ構造内のさまざまなタイプのツリーについて、以下で詳しく説明します。

1.一般的なツリー

一般的なツリーは、ノードが持つことができる子の数に仕様や制約がないことを特徴としています。 階層構造を持つツリーはすべて、一般ツリーとして分類できます。 ノードには複数の子を含めることができ、ツリーの方向には任意の組み合わせを使用できます。 ノードは、0からnまでの任意の次数にすることができます。

以下は、データ構造内の一般的なツリーの典型的な例であり、上部の「2」がルートノードです。

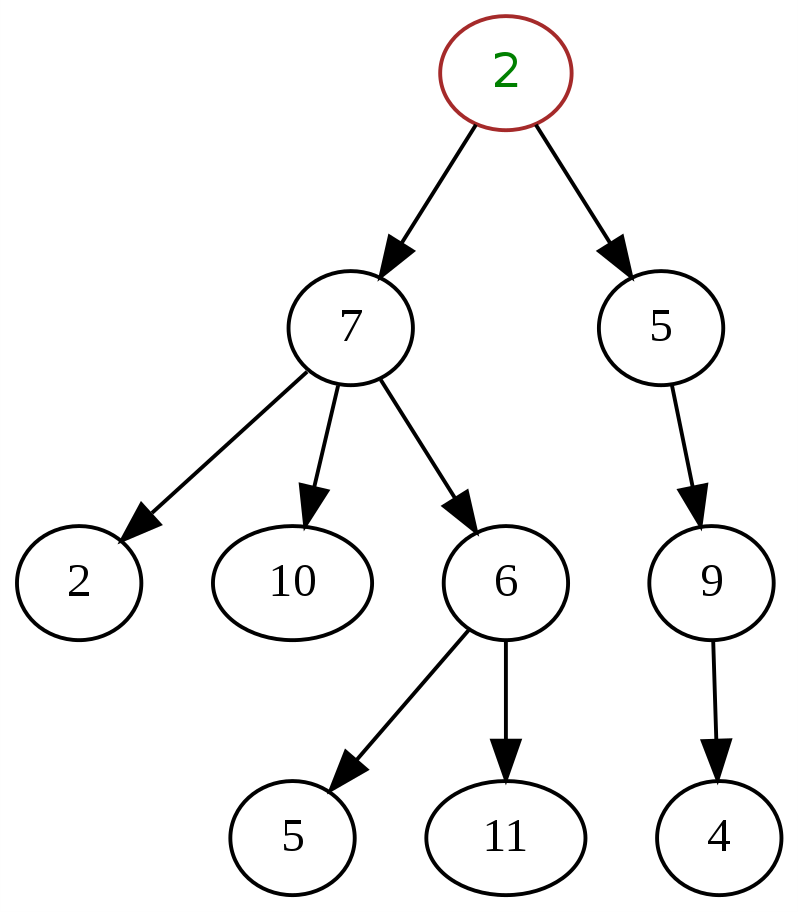
ソース

2.二分木

2つの数値を意味する「バイナリ」という単語で定義されているように、バイナリツリーは2つの子ノードを持つことができるノードで構成されます。 二分木のノードは、最大で0、1、または2つのノードを持つことができます。 データ構造の二分木は非常に機能的なADTであり、さらに多くのタイプに細分化できます。 これらは主に、次の2つの目的でデータ構造で使用されます。

1. 二分探索木で観察されるように、ノードにアクセスしてそれらにラベルを付けるため。
2. 分岐構造によるデータの表現用。

以下は、データ構造内のバイナリツリーの基本的な図です。

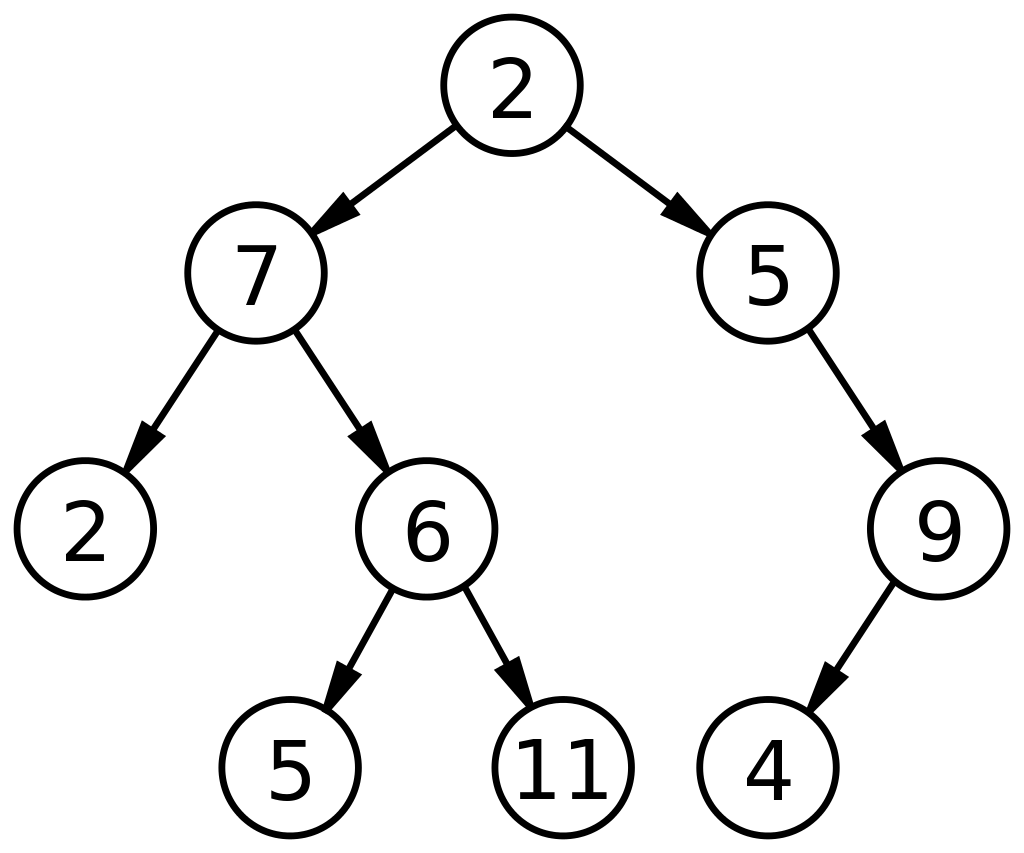
ソース

3.二分探索木

バイナリ検索ツリー（BST）は、データの検索/検索または追加/削除を高速化するように配置された、バイナリツリーの一意のサブタイプです。 BSTは、データ、その左の子、およびその右の子の3つのフィールドに基づくノードの表現によって定義されます。 BSTの支配要因は次のとおりです。

1. 左側のすべてのノード（左側の子）は、その親ノードよりも小さい値を保持する必要があります。
2. 右側のすべてのノード（右側の子）は、その親ノードよりも高い値を保持する必要があります。

このような配置により、配列で見られるように、検索時間が線形検索の半分に短縮されます。 したがって、データ構造内の二分探索木は、他のADTと比較して、検索と並べ替えに広く適用できます。

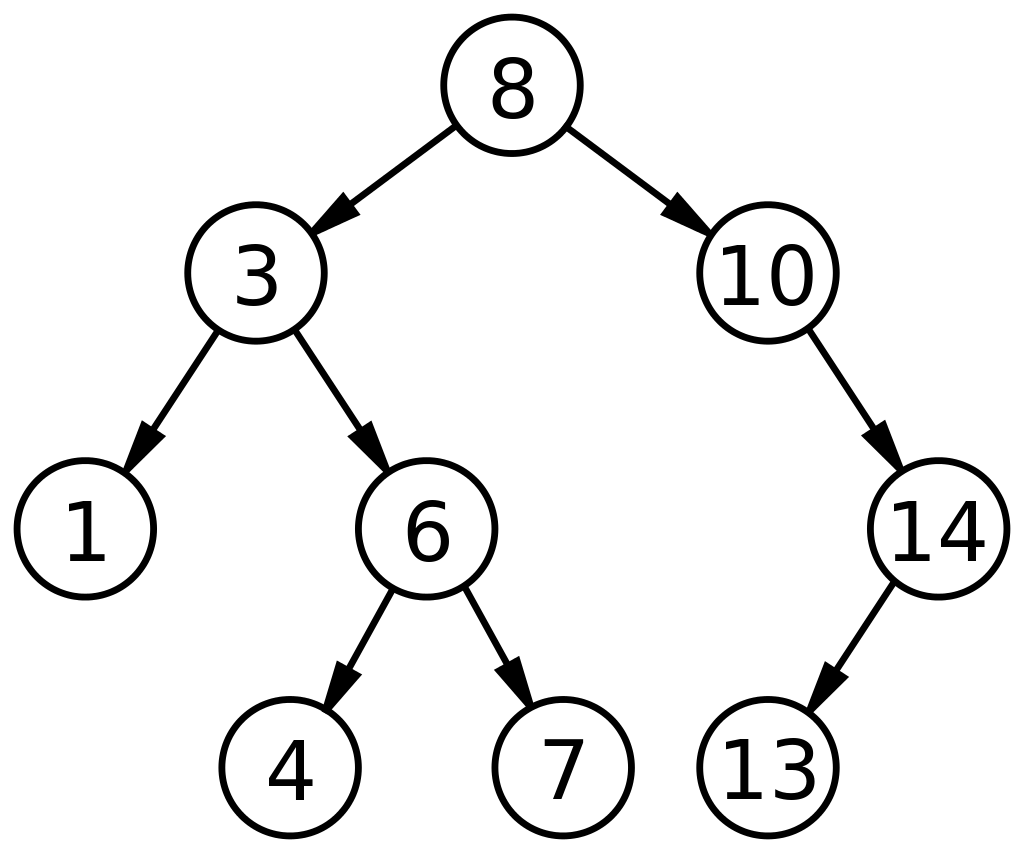
ソース

BTとBSTはどちらも本質的にデータ構造のツリーですが、名前の類似性に惑わされないでください。 upGradで、バイナリツリーとバイナリ検索ツリーの違いを詳しく調べてください。

4.AVLツリー

AVLツリーの名前は、その発明者であるAdelson-VelskyとLandisに由来しています。 AVLツリーは、自己平衡型の性質を備えています。 ルートノードの2つのサブツリーの高さは2未満に制限されています。 高さの差が1を超えると、子ノードのバランスが再調整されます。

AVLツリーは高さのバランスが取れており、このリバランスは1回転または2回転で発生します。 バランス係数は、左側のサブツリーと右側のサブツリーの高さの差であり、値は-1、0、および1です。

5.赤黒木

このタイプは、赤黒木も高さのバランスが取れているため、AVL木に似ています。 それらを分離するのは、バランスを取るために2回転以上を必要としないことです。 これらには、ノードの赤または黒の色を定義する追加のビットが含まれています。これにより、削除と挿入の際にツリーのバランスがとれます。 赤黒の色分けも変更中に再描画されますが、メモリの追加コストはほとんどありません。

6.スプレーツリー

二分探索木の別のサブタイプであるスプレー木には、回転操作を実行して最近のノードを調整するという独自の特性があります。 最近アクセスしたノードは、ローテーションを行うことでルートノードとして配置されます。 バランスの取れた木ですが、高さのバランスの取れた木ではありません。

木の回転は特定の方法で実行されるため、「スプレイ」の動作は、最初の二分木検索の後に実行されます。 すべての操作の後、ツリーはそれ自体のバランスをとるために回転され、検索された要素はルートノードとして一番上に配置されます。

7.治療

データ構造の「Treaps」は、ツリーとヒープの組み合わせです。 BSTでは、左側の子の値はルートノードよりも小さく、右側の子の値は高くする必要があります。 ヒープデータ構造では、ルートノードの値が最も低く、その子ノード（左と右の両方）の値が大きくなります。

したがって、treapは、キー（BSTに似ている）と優先度（ヒープに似ている）の形式で値を保持します。 最も優先度の高いノードは、優先度番号が独立した乱数になるように、最初にバイナリ検索ツリーに挿入されます。 それらは順序付けられたキーの動的なセットを維持し、それらのキー内でのバイナリ検索を可能にします。

8.Bツリー

データ構造内の自己平衡型ツリーとして、B-Treeはデータをソートして、対数時間での検索、順次アクセス、削除、および挿入を可能にします。 バイナリツリーとは異なり、Bツリーではノードに3つ以上の子を含めることができます。 これらは、より大きなデータブロックを読み書きするデータベースおよびファイルシステムと互換性があります。

データ構造のBツリーは、ディスクなどの大規模なストレージシステムに使用されます。 すべての葉には情報がなく、同じレベルに表示されます。 Bツリーの内部ノードは、範囲によってバインドされた可変サイズの子ノードを持つことができます。

これらは、データの流れを設計するプログラマーによって実装されるデータ構造のツリーです。 それらの独自の特性とアプリケーションを学ぶことは、データサイエンティストになるためのあなたの旅に不可欠です。 自分自身をスキルアップするもう1つの方法は、データ構造やその他の形式のADTのツリーに関する知識を必要とするさまざまなプロジェクトを通じて実践することです。

DSプロジェクトに知識を適用するために、次のブログリンクには、初心者向けの13の興味深いデータ構造プロジェクトのアイデアとトピックがあります[2021] 。

結論

データ構造内のツリーのような概念について学ぶのは難しい場合があり、プログラミング志願者は自分自身を教育するための専門家の指導が必要です。 データ構造内のツリーの詳細については、 upGradによるオンラインコースをご覧ください。 ソフトウェア開発のエグゼクティブPGプログラム– IIIT-BおよびupGradによるDevOpsを使用したDevOpsの専門化は、プログラマーとしてのキャリアを構築するのに役立ちます。

データ構造の習熟度はコーディングのプロセスに不可欠であるため、学生がエキスパートプログラマーおよびソフトウェア開発者になるのに役立ちます。 プログラマーとデータサイエンティストは、今後数十年の需要があります。

インドには5億人のインターネットユーザーがおり、大量のデータを生成および消費しているため、需要を満たすには数千人のデータサイエンティストを雇用する必要があります。 [2]これらのデータサイエンティストは、このセクター内での雇用を求めるために、関連する技術的専門知識を備えた適切な教育を必要としています。

upGrad＆IIIT-Bangaloreによってキュレーションされたソフトウェア開発のエグゼクティブPGプログラム–フルスタック開発の専門分野は、あなたのプロフィールを改善し、プログラマーとしてのより良い雇用機会を確保するのに役立ちます。