機械学習のためのナイーブベイズアルゴリズムを学ぶ[例を挙げて]
公開: 2021-02-25目次
序章
数学とプログラミングでは、通常、最も単純なソリューションのいくつかが最も強力なソリューションです。 単純ベイズアルゴリズムは、このステートメントの典型的な例です。 機械学習の分野で強力かつ急速な進歩と発展があったとしても、このナイーブベイズアルゴリズムは、最も広く使用されている効率的なアルゴリズムの1つとして依然として強力です。 単純ベイズアルゴリズムは、分類タスクや自然言語処理(NLP)の問題など、さまざまな問題でそのアプリケーションを見つけます。
ベイズの定理の数学的仮説は、このナイーブベイズアルゴリズムの背後にある基本的な概念として機能します。 この記事では、ベイズの定理の基本であるナイーブベイズアルゴリズムと、リアルタイムのサンプル問題を使用したPythonでの実装について説明します。 これらに加えて、競合他社と比較したナイーブベイズアルゴリズムのいくつかの長所と短所についても見ていきます。
確率の基本
ベイズの定理とナイーブベイズアルゴリズムの理解に取り掛かる前に、確率の基礎について既存の知識をブラッシュアップしましょう。
定義上、イベントAが与えられると、そのイベントが発生する確率はP(A)で与えられます。 確率的には、イベントAの発生がイベントBの発生確率を変更しない場合、およびその逆の場合、2つのイベントAおよびBは独立したイベントと呼ばれます。 一方、一方の発生によって他方の確率が変化する場合、それらは依存イベントと呼ばれます。
条件付き確率と呼ばれる新しい用語を紹介しましょう。 数学では、P(A | B)によって与えられる2つのイベントAとBの条件付き確率は、イベントBがすでに発生している場合のイベントAの発生確率として定義されます。 2つのイベントAとBの関係に応じて、それらが依存しているか独立しているかについて、条件付き確率は2つの方法で計算されます。
- 2つの従属イベントAおよびBの条件付き確率は、P(A | B)= P(AおよびB)/ P(B)で与えられます。
- 2つの独立したイベントAおよびBの条件付き確率の式は、次の式で与えられます。P(A | B)= P(A)
確率と条件付き確率の背後にある数学を知っているので、ベイズの定理に進みましょう。

ベイズの定理
統計と確率論では、ベイズの定理はベイズの定理とも呼ばれ、イベントの条件付き確率を決定するために使用されます。 言い換えると、ベイズの定理は、イベントに関連する可能性のある条件の事前知識に基づいて、イベントの確率を記述します。
より簡単に理解するには、家の価格の確率が非常に高いことを知る必要があると考えてください。 近くの学校、医療店、病院の存在など、他のパラメータがわかっている場合は、同じものをより正確に評価できます。 これはまさにベイズの定理が実行することです。
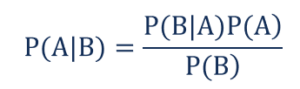
そのような、
- P(A | B)–イベントBが発生した場合の、イベントAの条件付き確率は、事後確率とも呼ばれます。
- P(B | A)–イベントAが発生した場合の、イベントBの条件付き確率は、尤度確率とも呼ばれます。
- P(A)–事前確率とも呼ばれるイベントAが発生する確率。
- P(B)–イベントBが発生する確率は、周辺確率とも呼ばれます。
'n'の独立変数を使用した単純な機械学習の問題があり、出力である従属変数がブール値(TrueまたはFalse)であるとします。 独立した属性が本質的にカテゴリであると仮定して、この例では2つのカテゴリを考えてみましょう。 したがって、これらのデータを使用して、尤度確率P(B | A)の値を計算する必要があります。
したがって、上記を観察すると、この機械学習モデルを学習するために2 *(2 ^ n -1 )パラメーターを計算する必要があることがわかります。 同様に、30個のブール独立属性がある場合、計算されるパラメーターの総数は30億に近くなり、計算コストが非常に高くなります。
ベイズの定理を使用して機械学習モデルを構築する際のこの困難は、ナイーブベイズアルゴリズムの誕生と発展につながりました。
ナイーブベイズアルゴリズム
実用的であるためには、ベイズの定理の上記の複雑さを減らす必要があります。 これは、ナイーブベイズアルゴリズムでいくつかの仮定を行うことによって正確に達成されます。 行われた仮定は、各機能が結果に独立した同等の貢献をするということです。
単純ベイズアルゴリズムは教師あり学習アルゴリズムであり、分類問題の解決に主に使用されるベイズの定理に基づいています。 これは、機械学習モデルを構築して迅速な予測を行う、最も単純で最も正確な分類器の1つです。 数学的には、イベントの確率関数を使用して予測を行うため、確率的分類子です。
問題の例
仮定の背後にあるロジックを理解するために、より良い直感を得るために簡単なデータセットを調べてみましょう。
| 色 | タイプ | 元 | 盗難? |
| 黒 | セダン | インポート | はい |
| 黒 | SUV | インポート | 番号 |
| 黒 | セダン | 国内の | はい |
| 黒 | セダン | インポート | 番号 |
| 茶色 | SUV | 国内の | はい |
| 茶色 | SUV | 国内の | 番号 |
| 茶色 | セダン | インポート | 番号 |
| 茶色 | SUV | インポート | はい |
| 茶色 | セダン | 国内の | 番号 |
上記のデータセットから、上記のナイーブベイズアルゴリズムに対して定義した2つの仮定の概念を導き出すことができます。
- 最初の仮定は、すべての機能が互いに独立しているということです。 ここでは、「赤」の色が車のタイプと原産地に依存しないなど、各属性が独立していることがわかります。
- 次に、各機能に同等の重要性を与えます。 同様に、車のタイプと起源についての知識だけでは、問題の出力を予測するのに十分ではありません。 したがって、どの変数も無関係ではなく、したがって、それらはすべて結果に等しく貢献します。
要約すると、Cが発生するという知識が与えられ、Aが発生するかどうかの知識がBの発生の可能性に関する情報を提供せず、Bが発生するかどうかの知識がAが発生する可能性。 これらの仮定により、ベイズアルゴリズムはナイーブになります。 そのため、名前はNaiveBayesAlgorithmです。
したがって、上記の問題の場合、ベイズの定理は次のように書き直すことができます–
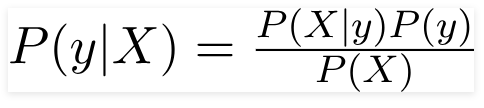
そのような、
- 車の色、タイプ、原点などの特徴を表す独立した特徴ベクトルX =(x 1 、x 2 、x3 ……xn ) 。
- 出力変数yには、YesまたはNoの2つの結果しかありません。
したがって、上記の値を代入することにより、ナイーブベイズ式は次のようになります。
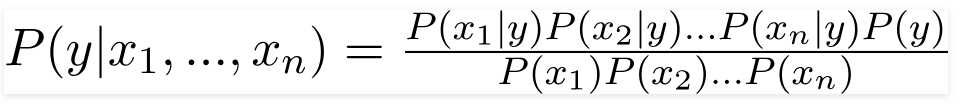
事後確率P(y | X)を計算するには、出力に対する属性ごとに度数分布表を作成する必要があります。 次に、度数分布表を尤度表に変換します。その後、最後に単純ベイズ方程式を使用して、各クラスの事後確率を計算します。 事後確率が最も高いクラスが予測の結果として選択されます。 以下は、3つの予測子すべての頻度と尤度の表です。
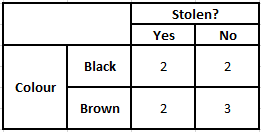
色の頻度表色の尤度表
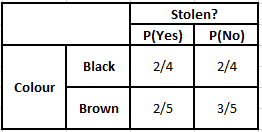
タイプの度数分布タイプの尤度テーブル
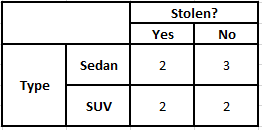
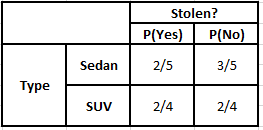
起源の頻度表起源の可能性表
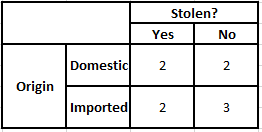
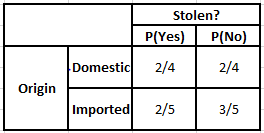

以下の条件の事後確率を計算する必要がある場合を考えてみましょう–
| 色 | タイプ | 元 |
| 茶色 | SUV | インポート |
したがって、上記の式から、以下に示すように事後確率を計算できます。
P(はい| X)= P(ブラウン|はい)* P(SUV |はい)* P(インポート|はい)* P(はい)
= 2/5 * 2/4 * 2/5 * 1
= 0.08
P(No | X)= P(Brown | No)* P(SUV | No)* P(Imported | No)* P(No)
= 3/5 * 2/4 * 3/5 * 1
= 0.18
上記の計算値から、「いいえ」の事後確率は「はい」よりも大きい(0.18> 0.08)ため、輸入元のSUVタイプであるブラウンカラーの車は「いいえ」に分類されると推測できます。 したがって、車は盗まれません。
Pythonでの実装
Naive Bayesアルゴリズムの背後にある数学を理解し、例を使用して視覚化したので、Python言語での機械学習コードを見ていきましょう。
関連:単純ベイズ分類器
問題分析
Pythonを使用した機械学習で単純ベイズ分類プログラムを実装するために、非常に有名な「アイリスフラワーデータセット」を使用します。 アイリスフラワーデータセットまたはフィッシャーのアイリスデータセットは、1998年に英国の統計学者、優生学者、生物学者のロナルドフィッシャーによって導入された多変量データセットです。これは、3つのクラスに関する情報を含む非常に少ない数値データで構成される、非常に小さく基本的なデータセットです。アイリス種に属する花の
- アイリスセトサ
- アイリスバーシカラー
- アイリスバージニカ
3つの種のそれぞれに50のサンプルがあり、合計150行のデータセットになります。 このデータセットで使用される4つの属性(または)独立変数は–
- がく片の長さ(cm)
- がく片の幅(cm)
- 花びらの長さ(cm)
- 花びらの幅(cm)
従属変数は、上記の4つの属性によって識別される花の「種」です。
ステップ1-ライブラリのインポート
いつものように、機械学習モデルを構築するための主なステップは、関連するライブラリをインポートすることです。 このために、データを前処理するためにNumPy、Mathplotlib、およびPandasライブラリをロードします。
numpyをnpとしてインポートします
matplotlib.pyplotをpltとしてインポートします
パンダをpdとしてインポートします
ステップ2–データセットのロード
ナイーブベイズ分類器のトレーニングに使用されるアイリスフラワーデータセットは、パンダデータフレームにロードされます。 4つの独立変数は変数Xに割り当てられ、最終的な出力種変数はyに割り当てられます。
データセット=pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc [:、:4] .values
y =dataset ['species']。valuesdataset.head(5)>>
sepal_length sepal_widthpetal_lengthpetal_width種
5.1 3.5 1.4 0.2 setosa
4.9 3.0 1.4 0.2 setosa
4.7 3.2 1.3 0.2 setosa
4.6 3.1 1.5 0.2 setosa
5.0 3.6 1.4 0.2 setosa
ステップ3–データセットをトレーニングセットとテストセットに分割する
データセットと変数を読み込んだ後、次のステップは、トレーニングプロセスを受ける変数を準備することです。 このステップでは、X変数とy変数をトレーニングデータセットとテストデータセットに分割する必要があります。 このために、データの80%をトレーニング目的で使用されるトレーニングセットにランダムに割り当て、残りの20%を、トレーニングされた単純ベイズ分類器の精度をテストするテストセットとして割り当てます。
sklearn.model_selectionからimporttrain_test_split
X_train、X_test、y_train、y_test = train_test_split(X、y、test_size = 0.2)
ステップ4–機能のスケーリング
これはこの小さなデータセットへの追加プロセスですが、より大きなデータセットで使用できるようにこれを追加しています。 この場合、トレーニングセットとテストセットのデータは、0〜1の範囲の値に縮小されます。これにより、計算コストが削減されます。
sklearn.preprocessingからインポートStandardScaler
sc = StandardScaler()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
ステップ5–トレーニングセットで単純ベイズ分類モデルをトレーニングする
このステップで、sklearnライブラリからNaiveBayesクラスをインポートします。 このモデルでは、ガウスモデルを使用します。ベルヌーイ、カテゴリカル、多項など、他のいくつかのモデルがあります。 したがって、X_trainとy_trainは、トレーニングの目的で分類変数に適合されます。
sklearn.naive_bayesからGaussianNBをインポート
分類子=GaussianNB()
classifier.fit(X_train、y_train)
ステップ6–テストセットの結果を予測する–
トレーニングされたモデルを使用してテストセットの種のクラスを予測し、種クラスの実際の値と比較します。
y_pred = classifier.predict(X_test)
df = pd.DataFrame({'実際の値':y_test、'予測値':y_pred})
df >>
実数値予測値
setosa setosa
setosa setosa
virginica virginica
versicolor versicolor
setosa setosa
setosa setosa
……………………
癜風
virginica virginica
setosa setosa
setosa setosa
versicolor versicolor
versicolor versicolor
上記の比較では、virginicaの代わりにVersicolorを予測した1つの誤った予測があることがわかります。
ステップ7–混同行列と精度
分類を扱っているので、分類器モデルを評価する最良の方法は、混同行列とその精度をテストセットに印刷することです。
sklearn.metricsからimportconfusion_matrix
cm = confusion_matrix(y_test、y_pred)from sklearn.metrics importaccuracy_score

print(“ Accuracy:“、accuracy_score(y_test、y_pred))
cm >>精度:0.9666666666666667
>> array([[14、0、0]、
[0、7、0]、
[0、1、8]])
結論
したがって、この記事では、単純ベイズアルゴリズムの基本を理解し、分類の背後にある数学を手作業で解決した例とともに理解しました。 最後に、単純ベイズ分類アルゴリズムを使用して人気のあるデータセットを解決するための機械学習コードを実装しました。
AI、機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのPGディプロマをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディと課題を提供します。 IIIT-B卒業生のステータス、5つ以上の実践的な実践的なキャップストーンプロジェクト、トップ企業との雇用支援。
確率は機械学習にどのように役立ちますか?
実際のシナリオでは、部分的または不完全な情報に基づいて決定を下さなければならない場合があります。 確率は、そのようなシステムの不確実性を定量化し、タスクのリスクを管理するのに役立ちます。 従来の方法は、特定のアクションの決定論的な結果に対してのみ機能しますが、予測モデルには常にある程度の不確実性があります。 この不確実性は、データのノイズなど、入力データの多くのパラメータに起因する可能性があります。 また、確率定理からのベイズビューは、入力データからのパターン認識に役立ちます。 このため、確率は最尤推定の概念を使用するため、関連する結果を生成するのに役立ちます。
混同行列の用途は何ですか?
混同行列は、分類モデルのパフォーマンスを解釈するために使用される2x2行列です。 これが機能するには、入力データの真の値がわかっている必要があるため、ラベルのないデータで表すことはできません。 これは、偽陽性(FP)、真陽性(TP)、偽陰性(FN)、および真陰性(TN)の数で構成されます。 予測は、トレーニングセットとテストセットからのカウントを使用してこれらのクラスに分類されます。 これは、精度、適合率、再現率、特異性などの有用なパラメーターを視覚化するのに役立ちます。 比較的理解しやすく、アルゴリズムについて明確なアイデアが得られます。
ナイーブベイズモデルのさまざまなタイプは何ですか?
すべてのタイプは、主にベイズの定理に基づいています。 ナイーブベイズモデルには、一般に、ガウス、ベルヌーイ、および多項の3つのタイプがあります。 Gaussian Naive Bayesは、入力パラメーターからの連続値を支援し、入力データのすべてのクラスが均一に分布していることを前提としています。 ベルヌーイのナイーブベイズは、データ機能が独立しており、ブール値で存在するイベントベースのモデルです。 多項ナイーブベイズもイベントベースのモデルに基づいています。 これは、イベントの発生に基づいて関連する頻度を表すベクトル形式のデータ機能を備えています。
