知っておくべきPythonで最もよく使われる7つの機械学習アルゴリズム

機械学習は、あらゆるデータで使用されているコンピューターアルゴリズムを処理する人工知能（AI）のブランチです。 そこに入力されたデータから自動的に学習することに焦点を当てており、毎回以前の予測を改善することで結果を得ることができます。

Pythonで使用される上位の機械学習アルゴリズム

以下は、Pythonで使用される主要な機械学習アルゴリズムの一部であり、コードスニペットとともに、分類境界の実装と視覚化を示しています。

1.線形回帰

線形回帰は、最も一般的に使用される教師あり機械学習手法の1つです。 その名前が示すように、この回帰は、線形方程式を使用して2つの変数間の関係をモデル化し、その線を観測データに適合させようとします。 この手法は、総売上高や住宅のコストなどの実際の連続値を推定するために使用されます。

最適な線は回帰直線とも呼ばれます。 これは次の式で与えられます。

Y = a * X + b

ここで、Yは従属変数、aは勾配、Xは独立変数、bは切片値です。 係数aとbは、さまざまなデータポイントと回帰直線方程式の間の距離の差の2乗を最小化することによって導出されます。

＃単純な回帰のための合成データセット

sklearn.datasetsからimportmake_regression

plt.figure（）

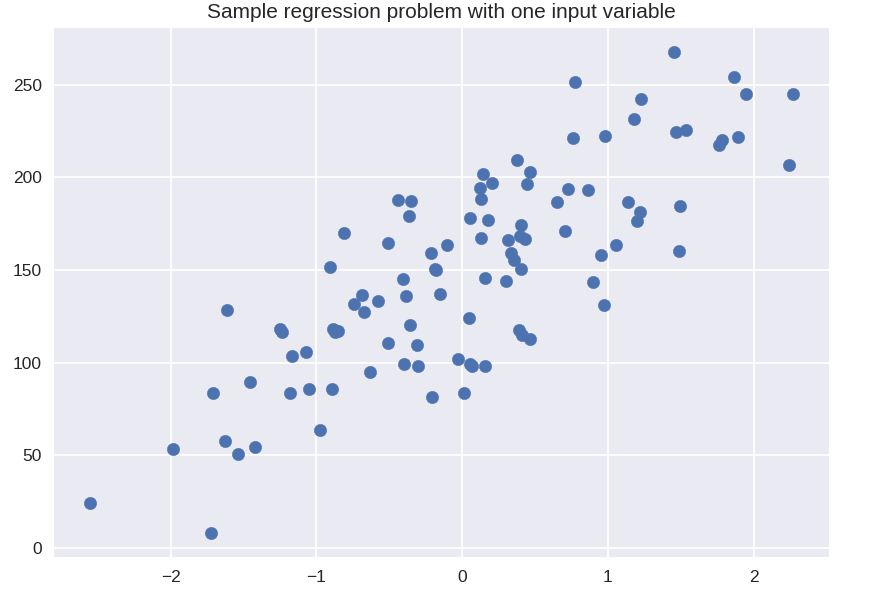
plt.title（ '1つの入力変数を使用したサンプル回帰問題'）

X_R1、y_R1 = make_regression（n_samples = 100、n_features = 1、n_informative = 1、bias = 150.0、noise = 30、random_state = 0）

plt.scatter（X_R1、y_R1、marker ='o'、s = 50）

plt.show（）

sklearn.linear_modelからimportLinearRegression

X_train、X_test、y_train、y_test = train_test_split（X_R1、y_R1、

random_state = 0）

linreg = LinearRegression（）。fit（X_train、y_train）

print（'線形モデル係数（w）：{}' .format（linreg.coef_））

print（'線形モデル切片（b）：{：.3f}' z.format（linreg.intercept_））

print（'決定係数スコア（トレーニング）：{：.3f}'。format（linreg.score（X_train、y_train）））

print（'決定係数スコア（テスト）：{：.3f}'。format（linreg.score（X_test、y_test）））

出力

線形モデル係数（w）：[45.71]

線形モデル切片（b）：148.446

決定係数スコア（トレーニング）：0.679

決定係数スコア（検定）：0.492

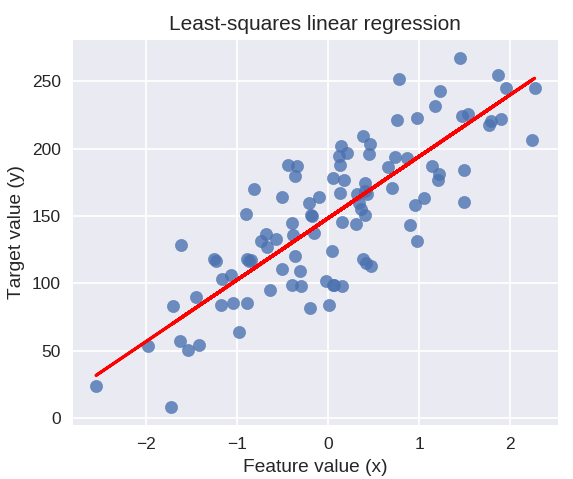
次のコードは、データポイントのプロットに近似回帰直線を描画します。

plt.figure（figsize =（5、4））

plt.scatter（X_R1、y_R1、marker ='o'、s = 50、alpha = 0.8）

plt.plot（X_R1、linreg.coef_ * X_R1 + linreg.intercept_、'r-'）

plt.title（'最小二乗線形回帰'）

plt.xlabel（'機能値（x）'）

plt.ylabel（'ターゲット値（y）'）

plt.show（）

分類手法を調査するための共通データセットの準備

次のデータは、Pythonの機械学習で最も一般的に使用されるさまざまな分類アルゴリズムを示すために使用されます。

UCIマッシュルームデータセットはmushrooms.csvに保存されます。

％matplotlibノートブック

パンダをpdとしてインポートします

numpyをnpとしてインポートします

matplotlib.pyplotをpltとしてインポートします

sklearn.decompositionからインポートPCA

sklearn.model_selectionからimporttrain_test_split

df = pd.read_csv（'readonly / mushrooms.csv'）

df2 = pd.get_dummies（df）

df3 = df2.sample（frac = 0.08）

X = df3.iloc [：、2：]

y = df3.iloc [：、1]

pca = PCA（n_components = 2）.fit_transform（X）

X_train、X_test、y_train、y_test = train_test_split（pca、y、random_state = 0）

plt.figure（dpi = 120）

plt.scatter（pca [y.values == 0、0]、pca [y.values == 0、1]、alpha = 0.5、label ='食用'、s = 2）

plt.scatter（pca [y.values == 1、0]、pca [y.values == 1、1]、alpha = 0.5、label ='有毒'、s = 2）

plt.legend（）

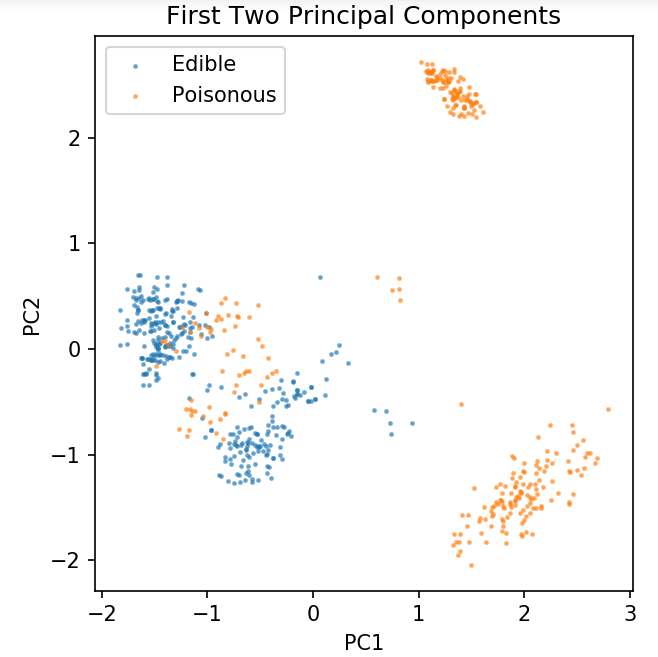
plt.title（'きのこデータセット\n最初の2つの主成分'）

plt.xlabel（'PC1'）

plt.ylabel（'PC2'）

plt.gca（）。set_aspect（'equal'）

以下に定義する関数を使用して、キノコのデータセットで使用するさまざまな分類子の決定境界を取得します。

def plot_mushroom_boundary（X、y、fitted_model）：

plt.figure（figsize =（9.8、5）、dpi = 100）

iの場合、enumerate（['Decision Boundary'、'Decision Probabilities']）のplot_type：

plt.subplot（1、2、i + 1）

mesh_step_size = 0.01＃メッシュのステップサイズ

x_min、x_max = X [：、0] .min（）– .1、X [：、0] .max（）+ .1

y_min、y_max = X [：、1] .min（）– .1、X [：、1] .max（）+ .1

xx、yy = np.meshgrid（np.arange（x_min、x_max、mesh_step_size）、np.arange（y_min、y_max、mesh_step_size））

i == 0の場合：

Z = fited_model.predict（np.c_ [xx.ravel（）、yy.ravel（）]）

そうしないと：

試す：

Z = fited_model.predict_proba（np.c_ [xx.ravel（）、yy.ravel（）]）[：、1]

それ外：

plt.text（0.4、0.5、'確率が利用できません'、horizo​​ntalalignment ='center'、verticalalignment ='center'、transform = plt.gca（）。transAxes、fontsize = 12）

plt.axis（'off'）

壊す

Z = Z.reshape（xx.shape）

plt.scatter（X [y.values == 0、0]、X [y.values == 0、1]、alpha = 0.4、label ='食用'、s = 5）

plt.scatter（X [y.values == 1、0]、X [y.values == 1、1]、alpha = 0.4、label ='Posionous'、s = 5）

plt.imshow（Z、interpolation ='nearest'、cmap ='RdYlBu_r'、alpha = 0.15、extent =（x_min、x_max、y_min、y_max）、origin ='lower'）

plt.title（plot_type +'\ n'+ str（fitted_model）.split（'（'）[0] +'テスト精度：' + str（np.round（fitted_model.score（X、y）、5）） ）。

plt.gca（）。set_aspect（'等しい'）;

plt.tight_layout（）

plt.subplots_adjust（top = 0.9、bottom = 0.08、wspace = 0.02）

2.ロジスティック回帰

線形回帰とは異なり、ロジスティック回帰は離散値（0/1バイナリ値、true / false、yes / no）の推定を扱います。 この手法は、ロジスティック回帰とも呼ばれます。 これは、ロジット関数を使用して特定のデータをトレーニングすることにより、イベントの確率を予測するためです。 その値は常に0と1の間にあります（確率を計算しているため）。

結果の対数オッズは、次のように予測変数の線形結合として構成されます。

オッズ=p/（1 – p）=イベントが発生する確率またはイベントが発生しない確率

ln（オッズ）= ln（p /（1 – p））

logit（p）= ln（p /（1 – p））= b0 + b1X1 + b2X2 +b3X3+…+bkXk

ここで、pは特性が存在する確率です。

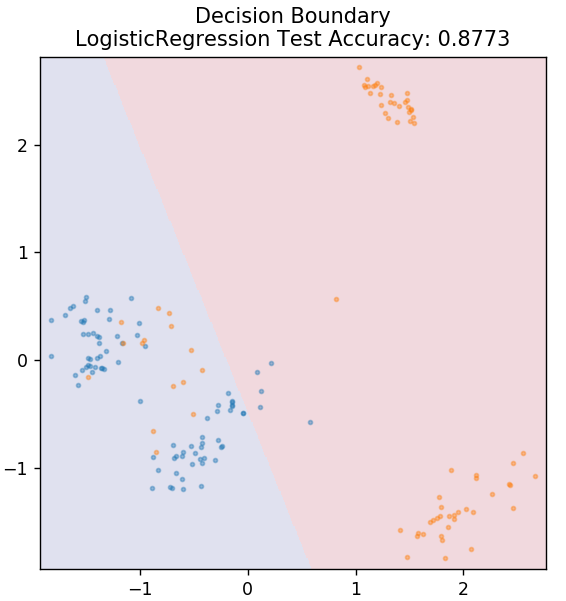
sklearn.linear_modelからimportLogisticRegression

モデル=LogisticRegression（）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

世界のトップ大学であるマスター、エグゼクティブポストグラデュエイトプログラム、ML＆AIの高度な証明書プログラムから人工知能の認定をオンラインで取得して、キャリアを早急に進めましょう。

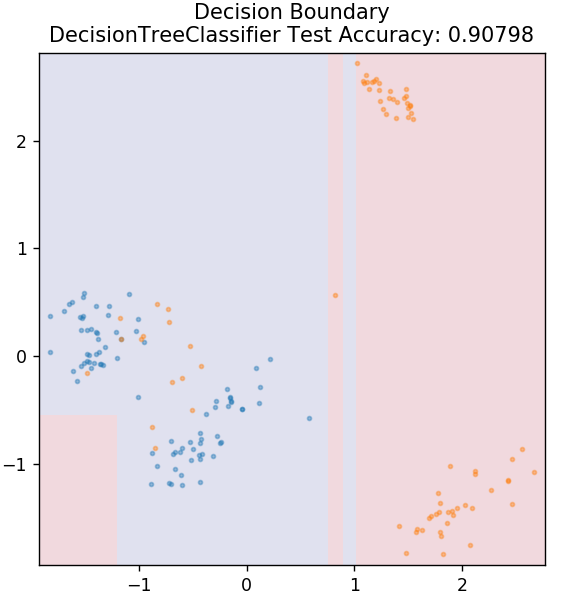
3.ディシジョンツリー

これは、データの連続変数と離散変数の両方を分類するために使用できる非常に一般的なアルゴリズムです。 すべてのステップで、データはいくつかの分割属性/条件に基づいて複数の同種のセットに分割されます。

sklearn.treeからインポートDecisionTreeClassifier

モデル=DecisionTreeClassifier（max_depth = 3）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

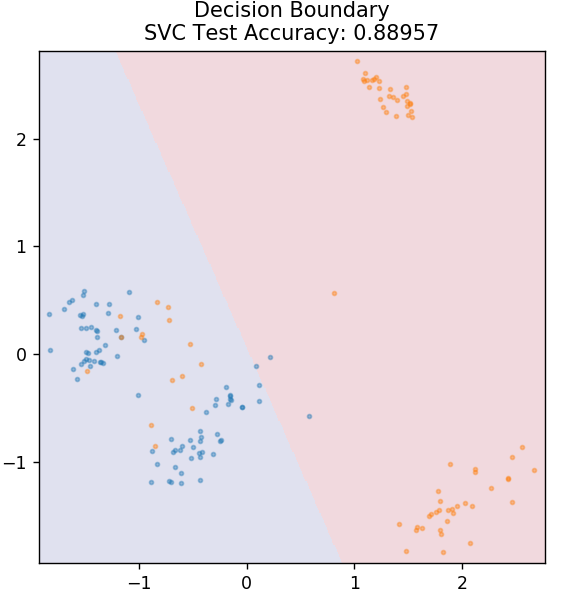
4.SVM

SVMはSupportVectorMachinesの略です。 ここでの基本的な考え方は、分離に超平面を使用してデータポイントを分類することです。 目標は、クラスまたはカテゴリの両方のデータポイント間の最大距離（またはマージン）を持つ超平面を見つけることです。

将来的に未知点を最も自信を持って分類できるように飛行機を選びます。 SVMは、非常に少ない計算能力で高精度を実現するため、有名に使用されています。 SVMは、回帰問題にも使用できます。

sklearn.svmからインポートSVC

モデル=SVC（カーネル='線形'）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

チェックアウト： GitHub上のPythonプロジェクト

5.ナイーブベイズ

名前が示すように、ナイーブベイズアルゴリズムはベイズの定理に基づく教師あり学習アルゴリズムです。 ベイズの定理は、条件付き確率を使用して、特定の知識に基づいてイベントの確率を提供します。

どこ、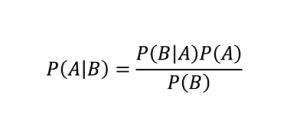

P（A | B）：イベントBがすでに発生している場合に、イベントAが発生する条件付き確率。 （事後確率とも呼ばれます）

P（A）：イベントAの確率。

P（B）：イベントBの確率。

P（B | A）：イベントAがすでに発生している場合に、イベントBが発生する条件付き確率。

なぜこのアルゴリズムはナイーブという名前なのですか？ これは、すべてのイベントの発生が互いに独立していることを前提としているためです。 したがって、各機能は、データポイント間の依存関係を持たずに、データポイントが属するクラスを個別に定義します。 ナイーブベイズは、テキストの分類に最適です。 少量のトレーニングデータでも十分に機能します。

sklearn.naive_bayesからGaussianNBをインポート

モデル=GaussianNB（）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

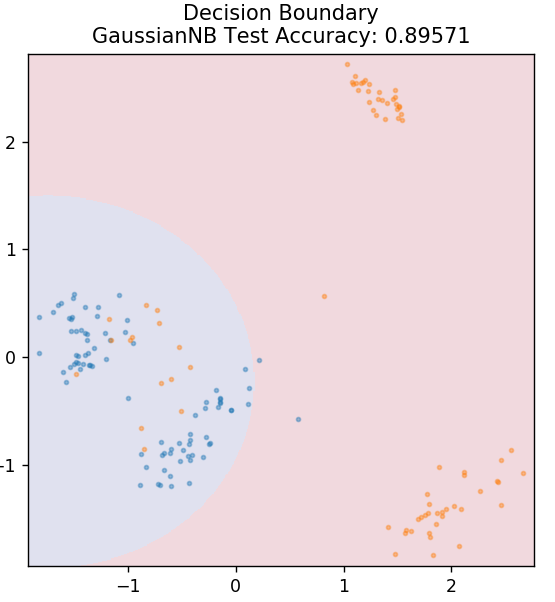
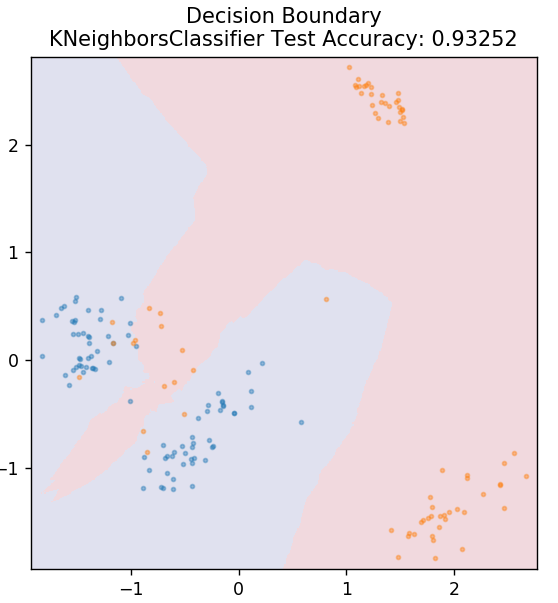
5.KNN

KNNはK最近傍法の略です。 これは、以前に分類されたトレーニングデータとの類似性に従ってテストデータを分類する、非常に広く使用されている教師あり学習アルゴリズムです。 KNNは、トレーニング中にすべてのデータポイントを分類するわけではありません。 代わりに、データセットを保存するだけで、新しいデータを取得すると、類似性に基づいてそれらのデータポイントを分類します。 これは、そのデータポイントのK個の最近傍（ここではn_neighbors ）のユークリッド距離を計算することによって行われます。

sklearn.neighborsからインポートKNeighborsClassifier

モデル=KNeighborsClassifier（n_neighbors = 20）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

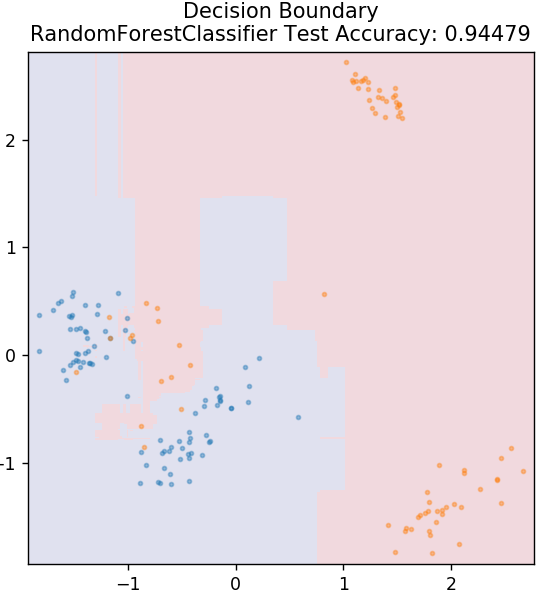
6.ランダムフォレスト

ランダムフォレストは、教師あり学習手法を使用する非常にシンプルで多様な機械学習アルゴリズムです。 名前から推測できるように、ランダムフォレストは、アンサンブルとして機能する多数の決定木で構成されています。 各決定木はデータポイントの出力クラスを把握し、モデルの最終出力として多数派クラスが選択されます。 ここでの考え方は、同じデータで作業するツリーが多いほど、個々のツリーよりも結果が正確になる傾向があるということです。

sklearn.ensembleからインポートRandomForestClassifier

model = RandomForestClassifier（）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

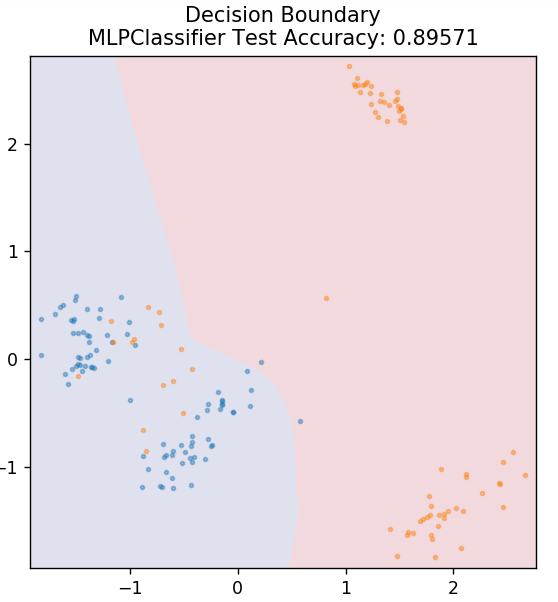
7.多層パーセプトロン

多層パーセプトロン（またはMLP）は、ディープラーニングの分野に属する非常に魅力的なアルゴリズムです。 より具体的には、フィードフォワード人工ニューラルネットワーク（ANN）のクラスに属します。 MLPは、入力層、出力層、および隠れ層の少なくとも3つの層を持つ複数のパーセプトロンのネットワークを形成します。 MLPは、非線形分離可能であるデータを区別することができます。

隠れ層の各ニューロンは、活性化関数を使用して次の層に進みます。 ここでは、バックプロパゲーションアルゴリズムを使用して、実際にパラメーターを調整し、ニューラルネットワークをトレーニングします。 これは主に単純な回帰問題に使用できます。

sklearn.neural_networkからインポートMLPClassifier

モデル=MLPClassifier（）

model.fit（X_train、y_train）

plot_mushroom_boundary（X_test、y_test、model）

また読む： Pythonプロジェクトのアイデアとトピック

結論

異なる機械学習アルゴリズムは異なる決定境界を生成し、したがって異なる精度は同じデータセットを分類する結果になると結論付けることができます。

一般に、あらゆる種類のデータに最適なアルゴリズムとして誰かのアルゴリズムを宣言する方法はありません。 機械学習では、各データセットに最適なものを個別に決定するために、さまざまなアルゴリズムについて厳密な試行錯誤が必要です。 MLアルゴリズムのリストは、明らかにここで終わりではありません。 PythonのScikit-Learnライブラリで探求されるのを待っている他のテクニックの膨大な海があります。 これらすべてを使用してデータセットをトレーニングし、楽しんでください。

デシジョンツリー、機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのエグゼクティブPGプログラムをご覧ください。このプログラムは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30以上のケーススタディを提供しています。課題、IIIT-B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。