確率密度関数の概要[式、プロパティ、アプリケーション、例]
公開: 2021-09-28確率密度関数(PDF)は、離散確率変数の確率分布を示す統計の式です。 確率分布は、簡単に言えば、株式やETFなどの確率変数の結果の尤度として定義できます。 離散変数は、正確な値を決定できる連続確率変数とは対照的に発生します。
たとえば、株式市場のスクリプトの値は、任意の数の小数点を持つ連続変数(例:65.7685434567)ではなく、離散確率変数に2つの小数点(たとえば、65.76)しかありません。
確率密度関数は、離散確率変数の結果の尤度を決定するために使用される統計ツールです。 グラフにプロットすると、PDFは、曲線の下の領域が結果の確率を表すベル曲線と同じように見えます。
グラフィックモデルとして投影された場合、曲線の下の領域は、離散確率変数の値が下がる範囲を表します。 したがって、曲線の下の総面積は、変数の結果の確率に等しくなります。
確率密度関数は、確率変数が特定の値の範囲内に入る可能性を判断できます。
通常、確率密度関数は、株式市場の特定のファンドに関連するリスクと潜在的な収益を分析します。

目次
確率密度関数と見なされる関数が満たすべき条件
離散変数の値は、無限の数の値を持つことができる連続変数とは対照的に、正確に測定できます。 確率密度関数であるためには、どの関数も以下の2つの条件を満たす必要があります。
- 確率変数の可能な各値のf(x)値は、正(非負)である必要があります。
- 曲線の総面積の積分値(確率変数のすべての可能な値の積分)は1である必要があります。
確率密度関数と確率分布関数の違い
確率変数は多くの値を持つことができます。 確率変数が持つことができる各可能な値の記述は、その確率分布と呼ばれます。
確率分布は、一連の結果とそれに関連する確率を示します。 連続確率分布を表す統計関数は、確率密度関数として知られています。
確率質量関数と呼ばれる離散確率分布を表す別の統計ツールがあります。 これにより、考えられるすべての結果とその可能性の確率について詳細に説明されます。
確率密度関数の式
確率変数が離散である場合、その確率分布は確率質量関数と呼ばれ、連続変数である場合、確率分布は確率密度関数と呼ばれます。
PDFは、問題の確率変数に可能な値の範囲がある場合に使用されます。 それらの確率分布は、正確な値を決定するために使用されます。
確率変数をXで表すとします。確率変数Xの確率密度関数fは、次のように表すことができます。
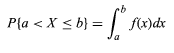
- 確率変数の値はaとbの間にあります。
- Xが範囲(区間)rおよびsから特定の数値を選択する確率を表す場合、確率密度関数は次のように表すことができます。
f ( x )= 1 /( s − r ) ( r < x < sの場合)およびf ( x )= 0 ( x < rまたはx > sの場合) 。
- PDFFは次のように表されます。
F ( x ) = P { X≤x } _
これは、Xの分布関数または累積分布関数と呼ばれます。
確率変数Xが確率分布関数f ( x )を持っていることを考えると、fとFの間の関係は次のように確立できます。
F ′(。 x )= f ( x )
離散確率変数の分布関数は、その確率分布関数とは異なります。 2つの関係は次のように表すことができます。

確率変数の期待値は、次のように表されます。
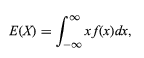

したがって、すべての離散変数と確率変数は、結合された理論の助けを借りて均一に扱うことができます。
確率密度関数の式
ある固定値xでの連続確率変数Xの確率は常に0です。この場合、P(X = x)は使用できません。 値の範囲(a、b)の間にあるXの値を決定する必要があります。 同じことを決定するために、次の式が使用されます。
![]()
確率密度関数のプロパティ
たとえば、範囲(a、b)の間の値をとる連続確率変数は、曲線の下の面積と、(a)を下限として、(b)をその下限としてプロットされたX軸を計算することによって推定されます。上限。 上記の確率密度関数は次のように表されます。
![]()
確率密度関数は、すべての可能な値に対して正(非負)です。 これは、すべてのxについてf(x)≥0を意味します。 密度曲線とX軸(横軸)の間にある面積は1です。
これは、次のように表すこともできます。
![]()
密度関数曲線は、一連の連続値または変数の定義域に対して明確に定義された、指定された範囲全体で連続しています。
世界のトップ大学(修士、エグゼクティブ大学院プログラム、ML&AIの高度な証明書プログラム)からオンラインで機械学習コースに参加して、キャリアを早急に進めましょう。
確率密度関数の応用
- 確率密度関数は、大気中のNO濃度レベルの年次モデリングで使用されます。
- ディーゼルエンジン燃焼のモデリング。
- 統計では、確率密度関数を使用して、確率変数の結果の可能性を判断します。
確率密度関数の例
例1
以下は、確率密度関数(PDF)を使用して株式市場への投資家のリスクの可能性を判断する方法の例です。
まず、PDFは履歴情報に基づいてグラフィックツールとして生成されます。
PDFの最も一般的な形式はニュートラルな予測であり、リスクはさまざまな可能性にわたって報酬と等しくなります。 リスクテイク能力の低い投資家は、限られた利益しか得られないため、ベルカーブの左側になります。 逆に、リスクテイク能力の高い投資家は、より高い利回りで報われる可能性が高いため、曲線の右側に分類されます。
ほとんどの投資家は平均的なリスクテイク能力を下回っているため、カーブの真ん中を占めています。
これは、受け取ったデータに基づいて投資家のカテゴリを分析するのに役立ちます。 これは、株式市場のブローカーが製品を販売する顧客のターゲットカテゴリを特定するのに役立ちます。
例2
確率密度関数の重要なアプリケーションの1つは、正規確率変数としても知られるガウス確率変数です。
どちらの場合も、グラフは確率密度関数のベル曲線を示します。
密度は次のように表すことができます

上記の密度方程式のグラフを以下に示します。


曲線の下の領域は、ガウス確率変数の実際の値を表します。
結論
確率密度関数は、機械学習で重要な役割を果たします。 機械学習と人工知能でのキャリアを目指す学生には、upGradのIIT-機械学習の高度な証明書プログラムに登録することを強くお勧めします。 このプログラムは、クラウドコンピューティングテクノロジーを使用して機械学習モデルを展開できるように、上級の専門家を対象にカスタマイズおよび設計されています。
カリキュラムは、学習プロセスをより適切で実用的なものにするために、IITマドラスの教員と業界の専門家によって設計されています。 このプログラムは、インドで切望され、1位にランクされているエンジニアリングカレッジから世界的に認められた認定と、upGradからの360度の配置サポートを提供します。
さらに、upGradの40,000人以上の有料学習者ベースで大規模なプロジェクトに協力する多くの機会が得られます。
私たちのウェブサイトにアクセスして、学習の旅を始めましょう!
確率密度関数を1より大きくすることはできますか?
確率関数は固定確率を与えるため、1を超えることはできません。ただし、PDF f(x)は、Xの特定の値に対して1より大きい値を持つことができます。これは、確率値(曲線の下の面積)であり、f(x)の正確な値ではありません。
確率密度関数から何を推測できますか?
確率密度関数は、離散確率変数の結果の可能性を判断するために使用される統計手法です。 PDFは、X軸とY軸に背景データがプロットされたグラフに表示されます。 グラフはベル曲線を示しています。 曲線の範囲は可能な値の範囲を示し、曲線の下の領域は離散確率変数の正確な値を提供します。
正規分布の確率密度関数はどうなりますか?
正規分布は対称であり、確率変数のすべての正の値と負の値に対してゼロ以外の確率があります。 平均が無視できるため、確率が3または4標準偏差を超える値に割り当てられている場合でも、ゼロ以外の確率は有効です。
