機械学習における多変量回帰の概要：完全ガイド

今日のテクノロジーがデータ駆動型であることは周知の事実です。 データは数字をまとめたものにすぎない場合がありますが、有意義に処理して、企業が長期的に競争力と持続可能性を維持するための生産性と機知を引き出すことができます。 たまたま、データ分析は生の情報から正確な見積もりを導き出すための答えです。

データ分析は、データを精査し、処理し、使用可能な形式に変換するための統計的および論理的なアイデアを含む手法です。 データ分析によって引き出されたソリューションは、重要な決定を行うためにビジネスで使用されます。 データサイエンスとデータ分析を使用して、将来の結果を高精度で予測します。 これは、科学技術とアルゴリズムを使用して、データのプールから実行可能な情報を取得するプロセスです。

データの専門家が直面する一般的な問題は、応答変数（Yで示される）と説明変数（Xiで示される）の間に統計的関係が存在するかどうかを判断する方法です。

この懸念に対する答えは回帰分析です。 これをさらに詳しく理解しましょう。

回帰分析とは何ですか？

回帰分析は、制御または教師あり機械学習アルゴリズムに従うデータ分析で一般的な方法の1つです。 これは、データ内の変数間の関係を識別して確立するための効果的な手法です。

回帰分析では、数学的戦略を使用して実行可能な変数を分類し、それらの分類された変数について非常に正確な結論を導き出します。

多変量回帰とは何ですか？

多変量は、複数のデータ変数を分析する制御または教師あり機械学習アルゴリズムです。 これは、1つの従属変数と多くの独立変数を含む重回帰の続きです。 出力は、独立変数の数に基づいて予測されます。

多変量回帰は、他の変数の変化に対する変数に存在する因子の同時応答を説明する式を計算します。 それらは、さまざまな分野のデータを研究するために使用されます。 たとえば、不動産では、多変量回帰を使用して、場所、部屋の数、利用可能な設備などのいくつかの要因に基づいて家の価格を予測します。

多変量回帰のコスト関数

コスト関数は、モデルの結果が観測データから逸脱した場合にサンプルにコストを割り当てます。 コスト関数の式は、予測値と実際の値の差の2乗の合計を、データセットの長さの2倍で割ったものです。

次に例を示します。

結果：

ソース

多変量回帰分析の使用方法は？

多変量回帰分析に含まれるプロセスには、特徴の選択、特徴のエンジニアリング、特徴の正規化、選択損失関数、仮説分析、および回帰モデルの作成が含まれます。

1. 機能の選択：これは、多変量回帰の最も重要なステップです。 変数選択とも呼ばれるこのプロセスでは、実行可能な変数を選択して効率的なモデルを構築します。
2. 機能の正規化：これには、合理化された分散とデータ比率を維持するための機能のスケーリングが含まれます。 これは、より良いデータ分析に役立ちます。 すべての機能の値は、要件に応じて変更できます。
3. 損失関数と仮説の選択：損失関数は、エラーを予測するために使用されます。 仮説の予測が実際の数値から変化すると、損失関数が機能します。 ここで、仮説は、特徴または変数から予測された値を表します。
4. 仮説パラメーターの固定：仮説のパラメーターは、損失関数を最小化し、より良い予測を強化するように固定または設定されます。
5. 損失関数の削減：データセットで損失を最小化するためのアルゴリズムを生成することにより、損失関数を最小化します。これにより、仮説パラメーターの変更が容易になります。 最急降下法は、損失を最小化するために最も一般的に使用されるアルゴリズムです。 損失の最小化が完了すると、アルゴリズムを他のアクションに使用することもできます。
6. 仮説関数の分析：値を予測するために重要であるため、仮説の関数を分析する必要があります。 関数が分析された後、テストデータでテストされます。

ここで、多変量​​回帰を使用できる2つの方法を見てみましょう。

1.多変量線形回帰

多変量線形回帰は単純な線形回帰に似ていますが、多変量線形回帰では、複数の独立変数が従属変数に寄与するため、計算で複数の係数が使用される点が異なります。

• これは、複数の確率変数間の数学的関係を導出するために使用されます。 1つの従属変数に関連付けられている複数の独立変数の数を説明します。
• 複数の独立変数の詳細は、それらが結果変数に与える影響を正確に予測するために使用されます。
• 多変量線形回帰モデルは、各データポイントの最良の近似を使用して、線形形式（直線の形式）で関係を生成します。
• 多変量線形回帰モデルの方程式は次のとおりです。

yi=β0+β1xi1+β2xi2+…+βpxip+

ここで、i = n個の観測値の場合：

ソース

線形回帰はいつ使用できますか？

線形回帰モデルは、一方が依存し、もう一方が独立している2つの連続変数がある場合にのみ使用できます。

独立変数は、従属変数の値または結果を決定するためのパラメーターとして使用されます。

2.多変量ロジスティック回帰

ロジスティック回帰は、複数の独立変数に基づいてバイナリ結果を予測するために使用されるアルゴリズムです。 バイナリ結果には2つの可能性があります。シナリオが発生する（1で表される）か、発生しない（0で表される）かのいずれかです。

ロジスティック回帰は、結果（または従属変数）が二分されるデータであるバイナリデータで作業するときに使用されます。

ロジスティック回帰はどこで使用できますか？

ロジスティック回帰は、主に分類の問題に対処するために使用されます。 たとえば、電子メールがスパムであるかどうか、特定のトランザクションが悪意のあるものであるかどうかを確認するため。 データ分析では、損失を最小限に抑えて利益を増やすための計算された意思決定を行うために使用されます。

多変量ロジスティック回帰は、1つの従属変数と複数の結果がある場合に使用されます。 これは、2つ以上の可能な結果があるという点で、ロジスティック回帰とは異なります。

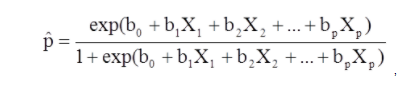
X1からXpは、別個の独立変数です。

b0からbpは回帰係数です

多重ロジスティック回帰モデルは、別の形式で記述することもできます。 以下のフォームでは、結果は、結果が存在するオッズの予想されるログです。

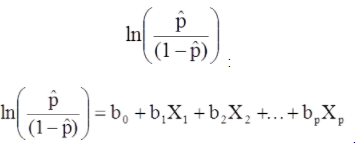
多重ロジスティック回帰モデルは、別の形式で記述することもできます。 以下の形式では、結果は、結果が存在するオッズの予想されるログです。

上記の方程式の右辺は線形回帰方程式に似ていますが、回帰係数を見つける方法が異なります。

多変量回帰モデルの仮定

• 従属変数と独立変数には線形関係があります。
• 独立変数は、それらの間で強い相関関係はありません。
• yiの観測値は、母集団からランダムかつ個別に選択されます。

多変量ロジスティック回帰モデルの仮定

• 従属変数は名義変数または順序変数です。 名目変数には、意味のある編成のない2つ以上のカテゴリがあります。 順序変数は2つ以上のカテゴリを持つこともできますが、構造があり、ランク付けすることができます。
• 順序変数、連続変数、または名義変数の1つまたは複数の独立変数が存在する可能性があります。 連続変数は、特定の範囲内で無限の値を持つことができる変数です。
• 従属変数は相互に排他的で網羅的です。
• 独立変数は、それらの間で強い相関関係はありません。

多変量回帰の利点

1. 多変量回帰は、データセット内の複数の変数間の関係を調査するのに役立ちます。
2. 従属変数と独立変数の間の相関は、結果の予測に役立ちます。
3. これは、機械学習で使用される最も便利で人気のあるアルゴリズムの1つです。

多変量回帰のデメリット

• 多変量手法の複雑さには、複雑な数学的計算が必要です。
• 損失とエラーの出力に矛盾があるため、多変量回帰モデルの出力を解釈するのは簡単ではありません。
• 多変量回帰モデルは、より小さなデータセットには適用できません。 大規模なデータセットに関しては、正確な出力を生成するように設計されています。

多変量回帰やその他の複雑なデータサイエンスの主題について詳しく知りたい場合は、upGradが最適なソリューションを提供します。 リバプールジョンムーア大学の18か月のデータサイエンスの理学修士コースは、500時間以上の厳格な学習時間、25回のコーチングセッション（1：8ベースで開催）、および20回以上のライブセッションをカバーしています。 upGradは、学生がキャリアを変革するための1：1の教育支援と360°のキャリアガイダンスサポートも提供しています。 学習者は、40,000人を超える有料学習者がいるグローバルプラットフォームでピアツーピア学習を活用し、6つの機能専門分野にわたる共同プロジェクトに取り組んで学習体験を最大化できます。