線形探索アルゴリズムの概要：概要と機能[例付き]

検索とは何ですか？

検索は、要素のリストから特定の要素を見つけるプロセスです。 特定のレコードの検索に役立ちます。 したがって、それは与えられたアイテムの場所を特定する技術です。 検索プロセスが成功するかどうかは、検索するアイテムが特定されているかどうかによって異なります。

データ構造により、2つの方法でデータを検索できます。

1. 線形検索または順次検索
2. 二分探索

線形探索

線形探索アルゴリズムは、データを順次探索するためのアルゴリズムの一種です。 このアルゴリズムは、O（n）の複雑さを持つ特定の要素を見つけます。 アイテムのコレクションに適用されます。 データのすべての項目が順番に検索され、検索された要素と一致する場合は返されます。 一致するものが見つからない場合、検索は収集されたデータの最後まで続行されます。 これは基本的に、リストをトラバースしながらすべての要素を探索する手法です。 検索アルゴリズムは、並べ替えられたデータと並べ替えられていないデータの両方に適用できます。 バイナリ検索アルゴリズムやハッシュテーブルなどの他の検索アルゴリズムによって提供される検索オプションが高速であるため、実際には線形検索が使用されることはめったにありません。

線形探索アルゴリズムのステップ

• ユーザーによる検索要素の読み取り。
• 検索する要素は、リストの最初の要素で圧縮されます。
• 要素が一致する場合、リターンが生成されます。
• 要素が一致しない場合、検索される要素はリストの2番目の要素と比較されます。
• 要素が一致するまで、このプロセスが繰り返されます。

線形探索アルゴリズムの特徴

1. これは通常、ソートされていない、または順序付けされていないデータの小さなリストに適用されます。
2. 時間は要素の数に線形依存するため、O（n）の場合は時間計算量が複雑になります。
3. 実装は非常に簡単です。

線形探索アルゴリズム

アイテムが見つからない限り、継続的なループ方式が続行されます

• アルゴリズムSeqnl_Search（list、item）
• 事前：リスト！=;
• 投稿：見つかった場合はアイテムのインデックスを返し、それ以外の場合は1
• インデックス<-fi
• while index <list.Cnt and list [index]！= item // cnt：counter variable
• インデックス<-インデックス+1
• 終了します
• index<list.Cntおよびlist[index]=itemの場合
• リターンインデックス
• 終了する場合
• リターン：1
• Seqnl_Searchを終了します

線形探索の例

問題： n個の要素の配列arr []が与えられた場合、arr[]内の特定の要素xを検索する関数を記述します。

図1：線形検索アルゴリズムの実装を示すコードの例

ソース

線形検索アルゴリズムは、いくつかのプログラミング言語で使用できます。

1. Pythonでの線形検索

図2： Python言語での線形検索アルゴリズムを示すコードの例

ソース

出力：要素はインデックス3に存在します

2. Cでの線形探索

図3： C言語での線形検索アルゴリズムを示すコードの例

ソース

出力：要素はインデックス3に存在します

3. データ構造の線形探索

データ構造の線形探索問題の擬似コードは次のとおりです。

図4：線形探索アルゴリズムの擬似コード

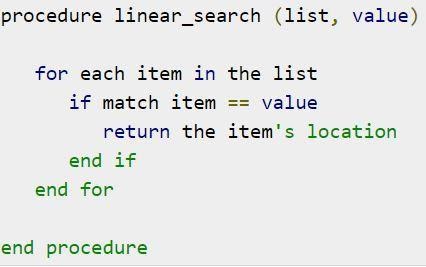
ソース

二分探索

二分探索は、要素の配列内の要素を検索するためのアルゴリズムです。 線形探索アルゴリズムと比較して、二分探索アルゴリズムは、ソートされたデータのリストに適用されます。

二分探索アルゴリズムには、次の手順が含まれます

• 検索する要素とリストまたは配列の中央にある要素との比較。
• 要素がリストの要素と一致する場合、中央の要素のインデックスを返します。
• 一致するものが返されない場合は、要素が中央の要素よりも大きいか小さいかがチェックされます。
• 中央の要素よりも大きな値の要素の場合、検索は配列の右側で実行されます。
• 同様に、要素の値が中央の要素よりも小さい場合、検索はリストの左側で実行されます。

したがって、二分探索は、データにソートされた方法で多数のロッド要素が含まれている場合に最適に適用されます。 これにより、検索アルゴリズムではリスト/配列を並べ替える必要があります。

二分探索の特徴

• 二分探索アルゴリズムは、配列内の多数の要素を検索する場合に役立ちます。
• 二分探索アルゴリズムの時間計算量はO（logn）です。
• 二分探索アルゴリズムの実装は簡単です。

二分探索アルゴリズム

• アルゴリズムBinary_Search（list、item）
• Lを0に、Rをnに設定：1
• L> Rの場合、Binary_Searchは失敗として終了します
• そうしないと
• m（中央要素の位置）を（L + R）/2の床に設定します
• Am <Tの場合、Lをm + 1に設定し、ステップ3に進みます。
• Am> Tの場合、Rをm：1に設定し、ステップ3に進みます。
• さて、Am = T、
• 検索が行われます。 リターン（m）

結論

この記事では、線形検索アルゴリズムとは何かを調べ、線形検索アルゴリズムを使用してリストから特定の要素を検索する方法についても詳しく学習しました。 最後に、Python 3を言語として使用して線形検索アルゴリズムを実際に実装し、目的の出力を取得する方法についても説明しました。

データサイエンスに興味がある場合は、IIIT-BとupGradのデータサイエンスのエグゼクティブPGプログラムをチェックする必要があります。このプログラムは、働く専門家向けに慎重に作成されており、多数のケーススタディ、実践的なワークショップ、1対1のメンターシップを提供しています。はるかに。