機械学習の最急降下法:どのように機能しますか?
公開: 2021-01-28目次
序章
機械学習の最も重要な部分の1つは、アルゴリズムの最適化です。 機械学習のほとんどすべてのアルゴリズムには、アルゴリズムのコアとして機能する最適化アルゴリズムがベースにあります。 ご存知のとおり、最適化は、実際のイベントを処理する場合や、市場でテクノロジーベースの製品を処理する場合でも、アルゴリズムの最終的な目標です。
現在、顔認識、自動運転車、市場ベースの分析など、いくつかのアプリケーションで使用されている最適化アルゴリズムがたくさんあります。同様に、機械学習では、このような最適化アルゴリズムが重要な役割を果たします。 そのような広く使用されている最適化アルゴリズムの1つは、この記事で説明する最急降下アルゴリズムです。
最急降下法とは何ですか?
機械学習では、最急降下法アルゴリズムは最も使用されているアルゴリズムの1つですが、それでもほとんどの新規参入者を困惑させます。 数学的には、最急降下法は、微分可能関数の極小値を見つけるために使用される1次の反復最適化アルゴリズムです。 簡単に言うと、この最急降下アルゴリズムは、コスト関数を可能な限り低くするために使用される関数のパラメーター(または係数)の値を見つけるために使用されます。 コスト関数は、構築された機械学習モデルの予測値と実際の値の間の誤差を定量化するために使用されます。
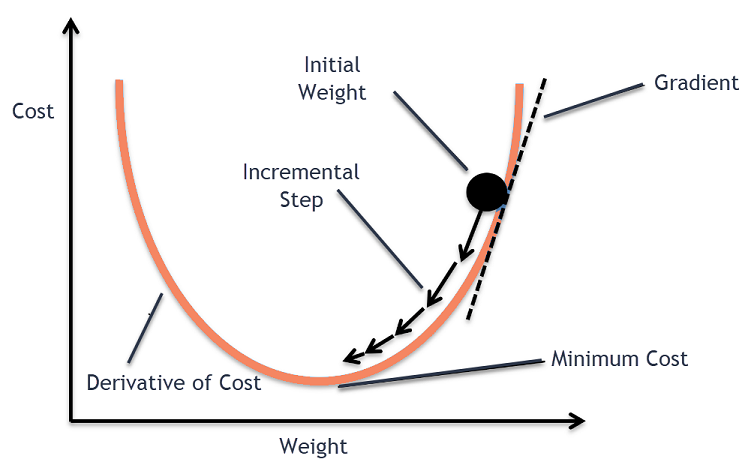
最急降下法の直感
通常は果物を保管したり、シリアルを食べたりする大きなボウルを考えてみましょう。 このボウルはコスト関数(f)になります。
これで、ボウルの表面の任意の部分のランダムな座標が、コスト関数の係数の現在の値になります。 ボウルの底は係数の最良のセットであり、関数の最小値です。
ここでの目標は、反復ごとに係数のさまざまな値を計算し、コストを評価して、より良いコスト関数値(より低い値)を持つ係数を選択することです。 複数の反復で、ボウルの底がコスト関数を最小化するための最良の係数を持っていることがわかります。

このように、最急降下アルゴリズムは最小のコストで機能します。
世界のトップ大学(修士、エグゼクティブ大学院プログラム、ML&AIの高度な証明書プログラム)からオンラインで機械学習コースに参加して、キャリアを早急に進めましょう。
最急降下法
最急降下法のこのプロセスは、最初にコスト関数の係数に値を割り当てることから始まります。 これは、0に近い値または小さなランダム値のいずれかです。
係数=0.0
次に、係数のコストは、それをコスト関数に適用し、コストを計算することによって取得されます。
コスト=f(係数)
次に、コスト関数の導関数が計算されます。 コスト関数のこの導関数は、微分計算の数学的概念によって得られます。 これは、導関数が計算される特定の点での関数の傾きを示します。 この勾配は、コスト値を低くするために、次の反復で係数をどの方向に移動するかを知るために必要です。 これは、計算された導関数の符号を観察することによって行われます。
デルタ=導関数(コスト)
計算された導関数からどちらの方向が下り坂であるかがわかったら、係数値を更新する必要があります。 このために、パラメータは学習パラメータとして知られており、アルファ(α)が利用されます。 これは、更新のたびに係数がどの程度変化するかを制御するために使用されます。
係数=係数–(アルファ*デルタ)
ソース
このようにして、係数のコストが0.0に等しくなるか、ゼロに十分近くなるまで、このプロセスが繰り返されます。 これは最急降下法アルゴリズムの手順です。
最急降下アルゴリズムの種類
現代では、現代の機械学習と深層学習アルゴリズムで使用される3つの基本的なタイプの勾配降下法があります。 これら3つのタイプのそれぞれの主な違いは、計算コストと効率です。 使用するデータの量、時間の複雑さ、および精度に応じて、次の3つのタイプがあります。
- バッチ勾配降下
- 確率的勾配降下法
- ミニバッチ最急降下法
バッチ勾配降下
これは、データセット全体を一度に使用してコスト関数とその勾配を計算する、勾配降下アルゴリズムの最初の基本バージョンです。 データセット全体が1回の更新で一度に使用されるため、このタイプの勾配の計算は非常に遅くなる可能性があり、デバイスのメモリ容量が不足しているデータセットでは不可能です。
したがって、このバッチ勾配降下アルゴリズムは、より小さなデータセットにのみ使用され、トレーニング例の数が多い場合、バッチ勾配降下は好ましくありません。 代わりに、確率的およびミニバッチ最急降下アルゴリズムが使用されます。

確率的勾配降下法
これは、反復ごとに1つのトレーニング例のみが処理される別のタイプの最急降下アルゴリズムです。 この場合、最初のステップはトレーニングデータセット全体をランダム化することです。 次に、係数を更新するために1つのトレーニング例のみが使用されます。 これは、すべてのトレーニング例が評価されたときにのみパラメーター(係数)が更新されるバッチ勾配降下法とは対照的です。
確率的勾配降下法(SGD)には、このタイプの頻繁な更新によって詳細な改善率が得られるという利点があります。 ただし、場合によっては、反復ごとに1つの例しか処理せず、反復回数が非常に多くなる可能性があるため、計算コストが高くなることがあります。
ミニバッチ最急降下法
これは最近開発されたアルゴリズムであり、バッチおよび確率的勾配降下アルゴリズムの両方よりも高速です。 これは、前述の両方のアルゴリズムの組み合わせであるため、ほとんどの場合に推奨されます。 この場合、トレーニングセットをいくつかのミニバッチに分割し、そのバッチの勾配を計算した後(SGDのように)、これらのバッチごとに更新を実行します。
通常、バッチサイズは30〜500の間で変化しますが、アプリケーションごとに異なるため、固定サイズはありません。 したがって、巨大なトレーニングデータセットがある場合でも、このアルゴリズムはそれを「b」ミニバッチで処理します。 したがって、反復回数が少ない大規模なデータセットに適しています。
'm'がトレーニング例の数である場合、b == mの場合、ミニバッチ勾配降下法はバッチ勾配降下法アルゴリズムと同様になります。
機械学習における最急降下法の変種
最急降下法のこの基礎に基づいて、これから開発された他のいくつかのアルゴリズムがあります。 それらのいくつかを以下に要約します。
バニラ最急降下法
これは、最急降下法の最も単純な形式の1つです。 バニラという名前は、純粋または偽和のないことを意味します。 この場合、コスト関数の勾配を計算することにより、最小値の方向に小さなステップが実行されます。 上記のアルゴリズムと同様に、更新ルールは次の式で与えられます。
係数=係数–(アルファ*デルタ)
勢いのある最急降下法
この場合、アルゴリズムは、次のステップに進む前に前のステップを知っているようなものです。 これは、前回の更新と運動量として知られる定数の積である新しい用語を導入することによって行われます。 この場合、重み更新ルールは次の式で与えられます。
更新=アルファ*デルタ
速度=previous_update*運動量
係数=係数+速度–更新

アダグラッド
ADAGRADという用語は、AdaptiveGradientAlgorithmの略です。 名前が示すように、それは重みを更新するために適応技術を使用します。 このアルゴリズムは、スパースデータに適しています。 この最適化は、トレーニング中のパラメーター更新の頻度に関連して学習率を変更します。 たとえば、勾配が高いパラメーターは、学習率が遅くなるように作成されているため、最小値をオーバーシュートすることはありません。 同様に、勾配が小さいほど学習率が高くなり、トレーニングが速くなります。
アダム
最急降下アルゴリズムにルーツを持つさらに別の適応最適化アルゴリズムは、適応モーメント推定の略であるADAMです。 これは、ADAGRADとSGDの両方とMomentumアルゴリズムの組み合わせです。 これはADAGRADアルゴリズムから構築されており、さらに欠点があります。 簡単に言えば、ADAM = ADAGRAD+Momentumです。
このように、AMSGrad、ADAMaxなど、世界で開発され、開発されている最急降下アルゴリズムには、他にもいくつかのバリエーションがあります。
結論
この記事では、機械学習で最も一般的に使用される最適化アルゴリズムの1つである最急降下アルゴリズムの背後にあるアルゴリズムと、開発されたそのタイプとバリアントについて説明しました。
upGradは、機械学習とAIのエグゼクティブPGプログラムと、機械学習とAIの理学修士を提供しており、キャリアの構築につながる可能性があります。 これらのコースでは、機械学習の必要性と、機械学習の最急降下法に至るまでのさまざまな概念をカバーするこのドメインの知識を収集するためのさらなる手順について説明します。
最急降下アルゴリズムはどこで最大に貢献できますか?
機械学習アルゴリズム内の最適化は、アルゴリズムの純度に応じて増加します。 最急降下アルゴリズムは、コスト関数エラーを最小限に抑え、アルゴリズムのパラメーターを改善するのに役立ちます。 勾配降下アルゴリズムは機械学習と深層学習で広く使用されていますが、その有効性は、データの量、優先される反復と精度の量、および利用可能な時間によって決定できます。 小規模なデータセットの場合、バッチ勾配降下法が最適です。 確率的勾配降下法(SGD)は、詳細でより広範なデータセットに対してより効率的であることが証明されています。 対照的に、Mini Batch Gradient Descentは、より迅速な最適化に使用されます。
最急降下法で直面する課題は何ですか?
機械学習モデルを最適化してコスト関数を減らすには、最急降下法が推奨されます。 ただし、欠点もあります。 モデル層の最小出力関数のために勾配が減少したと仮定します。 その場合、モデルが完全に再トレーニングされず、重みとバイアスが更新されないため、反復は効果的ではありません。 エラー勾配は、反復を最新の状態に保つために、重みとバイアスの負荷を蓄積することがあります。 ただし、このグラデーションは大きくなりすぎて管理できなくなり、爆発的なグラデーションと呼ばれます。 インフラストラクチャの要件、学習率のバランス、勢いに対処する必要があります。
最急降下法は常に収束しますか?
収束とは、最急降下アルゴリズムがコスト関数を最適なレベルに最小化することに成功したときです。 最急降下アルゴリズムは、アルゴリズムパラメータを介してコスト関数を最小化しようとします。 ただし、それは最適点のいずれかに着陸することができ、必ずしもグローバルまたはローカルの最適点を持っているとは限りません。 最適な収束が得られない理由の1つは、ステップサイズです。 より重要なステップサイズは、より多くの振動をもたらし、グローバル最適から逸脱する可能性があります。 したがって、最急降下法は常に最良の特徴に収束するとは限りませんが、それでも最も近い特徴点に到達します。
