機械学習におけるベイズの定理:はじめに、適用方法と例
公開: 2021-02-04目次
はじめに:ベイズの定理とは何ですか?
ベイズの定理は、確率を含む数学の分野である決定理論で幅広く働いた英国の数学者トーマス・ベイズにちなんで名付けられました。 ベイズの定理は、機械学習でも広く使用されており、クラスを正確かつ正確に予測するためのシンプルで効果的な方法です。 条件付き確率を計算するベイズ法は、分類タスクを含む機械学習アプリケーションで使用されます。
単純ベイズ分類として知られるベイズの定理の簡略化されたバージョンは、計算時間とコストを削減するために使用されます。 この記事では、これらの概念について説明し、機械学習におけるベイズの定理の適用について説明します。
世界のトップ大学であるマスター、エグゼクティブポストグラデュエイトプログラム、ML&AIの高度な証明書プログラムからオンラインで機械学習コースに参加して、キャリアを早急に進めましょう。
機械学習でベイズの定理を使用する理由
ベイズの定理は、条件付き確率、つまり、別のイベントがすでに発生している場合に1つのイベントが発生する確率を決定する方法です。 条件付き確率には追加の条件、つまりより多くのデータが含まれるため、より正確な結果に貢献できます。
したがって、条件付き確率は、機械学習で正確な予測と確率を決定するために必須です。 この分野がさまざまな分野でますます普及していることを考えると、機械学習におけるベイズの定理のようなアルゴリズムや手法の役割を理解することが重要です。
定理自体に入る前に、例を通していくつかの用語を理解しましょう。 書店のマネージャーが顧客の年齢と収入に関する情報を持っているとします。 彼は、本の売り上げが、若者(18〜35歳)、中年(35〜60歳)、高齢者(60歳以上)の3つの年齢層の顧客にどのように分布しているかを知りたいと考えています。

データをXと呼びましょう。ベイズの用語では、Xは証拠と呼ばれます。 いくつかの仮説Hがあり、特定のクラスCに属するいくつかのXがあります。
私たちの目標は、Xが与えられた場合の仮説Hの条件付き確率、つまりP(H | X)を決定することです。
簡単に言えば、P(H | X)を決定することにより、XがクラスCに属する確率を取得します。Xには年齢と収入の属性があります。たとえば、26歳で収入が$2000の場合です。 Hは、顧客が本を購入するという私たちの仮説です。
次の4つの用語に細心の注意を払ってください。
- 証拠–前述のように、P(X)は証拠として知られています。 この場合、顧客が26歳で、2000ドルを稼ぐ確率です。
- 事前確率–事前確率として知られるP(H)は、私たちの仮説の単純な確率です–つまり、顧客が本を購入するということです。 この確率には、年齢と収入に基づく追加の入力は提供されません。 計算はより少ない情報で行われるため、結果の精度は低くなります。
- 事後確率– P(H | X)は事後確率として知られています。 ここで、P(H | X)は、顧客がXを指定して本(H)を購入する確率です(彼は26歳で、$ 2000を稼いでいます)。
- 尤度– P(X | H)は尤度確率です。 この場合、顧客が本を購入することがわかっているとすると、尤度確率は、顧客が26歳で、収入が$2000である確率です。
これらを考えると、ベイズの定理は次のように述べています。
P(H | X)= [P(X | H)* P(H)] / P(X)
定理における上記の4つの項(事後確率、尤度確率、事前確率、および証拠)の出現に注意してください。
読む:ナイーブベイズの説明
機械学習にベイズの定理を適用する方法
ベイズの定理の簡略版である単純ベイズ分類器は、データをさまざまなクラスに正確かつ迅速に分類するための分類アルゴリズムとして使用されます。
単純ベイズ分類器を分類アルゴリズムとして適用する方法を見てみましょう。
- 一般的な例を考えてみましょう。Xは「n」属性で構成されるベクトルです。つまり、X = {x1、x2、x3、…、xn}です。
- 'm'クラス{C1、C2、…、Cm}があるとします。 分類器は、Xが特定のクラスに属することを予測する必要があります。 事後確率が最も高いクラスが最良のクラスとして選択されます。 したがって、数学的には、分類器はクラスCi iff P(Ci | X)> P(Cj | X)を予測します。 ベイズの定理の適用:
P(Ci | X)= [P(X | Ci)* P(Ci)] / P(X)
- P(X)は、条件に依存しないため、クラスごとに一定です。 したがって、P(Ci | X)を最大化するには、[P(X | Ci)* P(Ci)]を最大化する必要があります。 すべてのクラスが同じように発生する可能性があることを考慮すると、P(C1)= P(C2)= P(C3)…= P(Cn)になります。 したがって、最終的には、P(X | Ci)のみを最大化する必要があります。
- 一般的な大規模なデータセットには複数の属性がある可能性が高いため、属性ごとにP(X | Ci)操作を実行すると計算コストが高くなります。 ここで、クラス条件付き独立が問題を単純化し、計算コストを削減するために役立ちます。 クラス条件付き独立とは、属性の値が条件付きで互いに独立していると見なすことを意味します。 これは単純ベイズ分類器です。
P(Xi | C)= P(x1 | C)* P(x2 | C)*…* P(xn | C)
これで、より小さな確率を簡単に計算できます。 ここで注意すべき重要な点の1つは、xkは各属性に属しているため、処理している属性がカテゴリ型か連続型かを確認する必要もあります。
- カテゴリ属性がある場合、物事はより単純になります。 属性kの値xkで構成されるクラスCiのインスタンスの数を数え、それをクラスCiのインスタンスの数で割ることができます。
- 連続属性がある場合、正規分布関数があることを考慮して、次の式を適用します。 および標準偏差?:
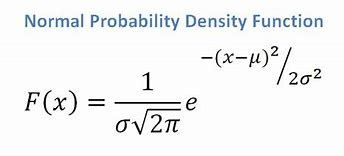

ソース
最終的には、P(x | Ci)= F(xk、?k、?k)になります。
- これで、クラスCiごとにベイズの定理を使用するために必要なすべての値が得られました。 予測されるクラスは、最高の確率P(X | Ci)* P(Ci)を達成するクラスになります。
例:書店の顧客を予測的に分類する
書店からの次のデータセットがあります。
| 年 | 所得 | 学生 | 信用格付け | Buys_Book |
| 若者 | 高い | 番号 | 公平 | 番号 |
| 若者 | 高い | 番号 | 優れた | 番号 |
| 中年 | 高い | 番号 | 公平 | はい |
| シニア | 中くらい | 番号 | 公平 | はい |
| シニア | 低い | はい | 公平 | はい |
| シニア | 低い | はい | 優れた | 番号 |
| 中年 | 低い | はい | 優れた | はい |
| 若者 | 中くらい | 番号 | 公平 | 番号 |
| 若者 | 低い | はい | 公平 | はい |
| シニア | 中くらい | はい | 公平 | はい |
| 若者 | 中くらい | はい | 優れた | はい |
| 中年 | 中くらい | 番号 | 優れた | はい |
| 中年 | 高い | はい | 公平 | はい |
| シニア | 中くらい | 番号 | 優れた | 番号 |
年齢、収入、学生、信用格付けなどの属性があります。 私たちのクラスbuys_bookには、「はい」または「いいえ」の2つの結果があります。
私たちの目標は、次の属性に基づいて分類することです。
X = {年齢=若者、学生=はい、収入=中、credit_rating=公正}。
前に示したように、P(Ci | X)を最大化するには、i=1およびi=2の場合に[P(X | Ci)* P(Ci)]を最大化する必要があります。
したがって、P(buys_book = yes)= 9/14 = 0.643
P(buys_book = no)= 5/14 = 0.357
P(年齢=若者| Buys_book =はい)= 2/9 = 0.222
P(年齢=若者| Buys_book =いいえ)= 3/5 = 0.600
P(収入=中| Buys_book =はい)= 4/9 = 0.444
P(収入=中| Buys_book =いいえ)= 2/5 = 0.400
P(学生=はい| Buys_book =はい)= 6/9 = 0.667
P(学生=はい| Buys_book =いいえ)= 1/5 = 0.200
P(credit_rating = fair | Buys_book = yes)= 6/9 = 0.667
P(credit_rating = fair | Buys_book = no)= 2/5 = 0.400
上で計算された確率を使用して、
P(X | Buys_book = yes)= 0.222 x 0.444 x 0.667 x 0.667 = 0.044
同様に、
P(X | Buys_book = no)= 0.600 x 0.400 x 0.200 x 0.400 = 0.019
Ciはどのクラスで最大のP(X | Ci)* P(Ci)を提供しますか? 計算します:
P(X | Buys_book = yes)* P(buys_book = yes)= 0.044 x 0.643 = 0.028
P(X | Buys_book = no)* P(buys_book = no)= 0.019 x 0.357 = 0.007

上記の2つを比較すると、0.028> 0.007であるため、単純ベイズ分類器は、上記の属性を持つ顧客が本を購入すると予測します。
チェックアウト:機械学習プロジェクトのアイデアとトピック
ベイジアン分類器は良い方法ですか?
機械学習におけるベイズの定理に基づくアルゴリズムは、他のアルゴリズムに匹敵する結果を提供し、ベイズ分類器は一般に単純な高精度の方法と見なされます。 ただし、ベイズ分類器は、クラス条件付き独立の仮定が有効であり、すべての場合に当てはまるわけではない場合に特に適切であることを覚えておく必要があります。 もう1つの実際的な懸念は、すべての確率データを取得することが常に実行可能であるとは限らないことです。
結論
ベイズの定理は、機械学習、特に分類ベースの問題に多くの用途があります。 このアルゴリズムファミリーを機械学習に適用するには、事前確率や事後確率などの用語に精通している必要があります。 この記事では、ベイズの定理の基本、機械学習の問題での使用について説明し、分類の例を使用しました。
ベイズの定理は機械学習の分類ベースのアルゴリズムの重要な部分を形成しているため、機械学習とNLPでupGradの高度な証明書プログラムについて詳しく知ることができます。 このコースは、機械学習に関心のあるさまざまな種類の学生を念頭に置いて作成されており、1-1のメンターシップなどを提供しています。
機械学習でベイズの定理を使用するのはなぜですか?
ベイズの定理は、条件付き確率、または以前に別のイベントが発生した場合に1つのイベントが発生する可能性を計算するための方法です。 条件付き確率は、追加の条件、つまりより多くのデータを含めることで、より正確な結果につながる可能性があります。 機械学習で正しい推定と確率を取得するには、条件付き確率が必要です。 幅広い分野でこの分野の普及が進んでいることを考えると、機械学習におけるベイズの定理のようなアルゴリズムやアプローチの重要性を理解することが重要です。
ベイジアン分類器は良い選択ですか?
機械学習では、ベイズの定理に基づくアルゴリズムが他の方法と同等の結果を生成し、ベイズ分類器は単純な高精度アプローチと広く見なされています。 ただし、ベイズ分類器は、すべての状況ではなく、クラス条件付き独立の条件が正しい場合に最適に使用されることを覚えておくことが重要です。 もう1つの考慮事項は、すべての尤度データを取得できるとは限らないことです。
ベイズの定理を実際にどのように適用できますか?
ベイズの定理は、それに関連している、または関連している可能性のある新しい証拠に基づいて発生の可能性を計算します。 この方法は、新しい情報が真であると仮定して、仮想の新しい情報がイベントの可能性にどのように影響するかを確認するためにも使用できます。 たとえば、52枚のカードのデッキから選択された1枚のカードを考えてみましょう。 カードがキングになる確率は、4を52で割った値(1/13)、つまり約7.69パーセントです。 デッキには4人の王が含まれていることに注意してください。 選択したカードがフェイスカードであることが明らかになったとしましょう。 デッキには12枚のフェイスカードがあるので、選んだカードがキングである確率は4を12で割ったもの、つまりおよそ33.3パーセントです。
