例で説明されたベイズの定理–完全ガイド

序章

ベイズの定理とは何ですか？

ベイズの定理は、直感が失敗することが多い条件付き確率の計算に使用されます。 確率で広く使用されていますが、この定理は機械学習の分野でも適用されています。 機械学習での使用には、モデルをトレーニングデータセットに適合させ、分類モデルを開発することが含まれます。

条件付き確率とは何ですか？

条件付き確率は通常、別のイベントが発生した場合の1つのイベントの確率として定義されます。

• AとBが2つのイベントである場合、条件付き確率はP（AがBとして与えられる）またはP（A | B）として指定されます。
• 条件付き確率は、同時確率（A | B）= P（A、B）/ P（B）から計算できます。

• 条件付き確率は対称的ではありません。 たとえば、P（A | B）！= P（B | A）

条件付き確率を計算する他の方法には、他の条件付き確率を使用することが含まれます。

P（A | B）= P（B | A）* P（A）/ P（B）

リバースも使用されます

P（B | A）= P（A | B）* P（B）/ P（A）

この計算方法は、同時確率の計算が難しい場合に役立ちます。 そうでなければ、逆条件付き確率が利用可能である場合、これによる計算が容易になります。

この条件付き確率の代替計算は、ベイズの定理またはベイズの定理と呼ばれます。 それは最初にそれを説明した人、「トーマス・ベイズ牧師」にちなんで名付けられました。

ベイズの定理の公式

ベイズの定理は、同時確率が利用できない場合に条件付き確率を計算する方法です。 分母に直接アクセスできない場合があります。 このような場合、別の計算方法は次のとおりです。

P（B）= P（B | A）* P（A）+ P（B | not A）* P（not A）

これは、P（B）の代替計算を示すベイズの定理の定式化です。

P（A | B）= P（B | A）* P（A）/ P（B | A）* P（A）+ P（B | not A）* P（not A）

上記の式は、分母を角かっこで囲んで説明できます。

P（A | B）= P（B | A）* P（A）/（P（B | A）* P（A）+ P（B | not A）* P（not A））

また、P（A）がある場合、P（Aではない）は次のように計算できます。

P（Aではない）= 1 – P（A）

同様に、P（not B | not A）がある場合、P（B | not A）は次のように計算できます。

P（B | not A）= 1 – P（not B | not A）

条件付き確率のベイズの定理

ベイズの定理は、方程式での適用のコンテキストに基づいて名前が付けられたいくつかの用語で構成されています。

事後確率はP（A | B）の結果を指し、事前確率はP（A）を指します。

• P（A | B）：事後確率。
• P（A）：事前確率。

同様に、P（B | A）とP（B）は尤度と証拠と呼ばれます。

• P（B | A）：可能性。
• P（B）：証拠。

したがって、条件付き確率のベイズの定理は次のように言い換えることができます。

事後=尤度*事前/証拠

煙がある場合に火災が発生する確率を計算する必要がある場合は、次の式が使用されます。

P（火|煙）= P（煙|火）* P（火）/ P（煙）

ここで、P（Fire）は事前、P（Smoke | Fire）は尤度、P（Smoke）は証拠です。

ベイズの定理の図

ベイズの定理の例は、問題でのベイズの定理の使用を説明するために説明されています。

問題

A、B、およびCのラベルが付いた3つのボックスがあります。 ボックスの詳細は次のとおりです。

• ボックスAには、2つの赤と3つの黒のボールが含まれています
• ボックスBには、3つの赤と1つの黒のボールが含まれています
• ボックスCには、1つの赤いボールと4つの黒いボールが含まれています

3つのボックスはすべて同一であり、ピックアップされる確率は同じです。 したがって、ボックスAから赤いボールが拾われた確率はどれくらいですか？

解決

Eは赤いボールが拾われたイベントを示し、A、B、Cはボールがそれぞれのボックスから拾われたことを示します。 したがって、条件付き確率はP（A | E）になり、計算する必要があります。

すべてのボックスが選択される確率が等しいため、既存の確率P（A）= P（B）= P（C）=1/3。

P（E | A）=ボックスAの赤いボールの数/ボックスAのボールの総数= 2/5

同様に、P（E | B）= 3/4およびP（E | C）= 1/5

次に、証拠P（E）= P（E | A）* P（A）+ P（E | B）* P（B）+ P（E | C）* P（C）

=（2/5）*（1/3）+（3/4）*（1/3）+（1/5）*（1/3）= 0.45

したがって、P（A | E）= P（E | A）* P（A）/ P（E）=（2/5）*（1/3）/ 0.45 = 0.296

ベイズの定理の例

ベイズの定理は、「テスト」に関する特定の情報を使用して「イベント」の確率を示します。

• 「イベント」と「テスト」には違いがあります。 たとえば、肝疾患の検査がありますが、これは実際に肝疾患を患っているのとは異なります。つまり、イベントです。
• まれなイベントでは、偽陽性率が高くなる可能性があります。

例1

彼らがアルコール依存症である場合、患者が肝疾患を患う確率はどれくらいですか？

ここで、「アルコール依存症」とは、肝疾患の「検査」（リトマス試験の一種）です。

• Aは「患者が肝疾患を持っている」というイベントです。

クリニックの以前の記録によると、クリニックに入る患者の10％が肝疾患に苦しんでいると述べています。

したがって、P（A）= 0.10

• Bは、「患者はアルコール依存症である」というリトマス試験です。

クリニックの以前の記録は、クリニックに入る患者の5％がアルコール依存症であることを示しました。

したがって、P（B）= 0.05

• また、肝疾患と診断された患者の7％はアルコール依存症です。 これはB|Aを定義します：彼らが肝臓病を持っていると仮定すると、患者がアルコール依存症である確率は7％です。

として、ベイズの定理の公式によると、

P（A | B）=（0.07 * 0.1）/0.05 = 0.14

したがって、アルコール依存症の患者の場合、肝疾患を患う可能性は0.14（14％）です。

例2

• 危険な火災はまれです（1％）
• しかし、バーベキューのために煙はかなり一般的です（10％）、
• そして危険な火災の90％が煙を出します

煙がある場合の危険な火災の確率はどれくらいですか？

計算

P（火|煙）= P（火）P（煙|火）/ P（煙）

= 1％x 90％/ 10％

= 9％

例3

日中の雨の可能性はどのくらいですか？ ここで、雨は日中の雨を意味し、雲は曇りの朝を意味します。

雲が与えられた場合の雨の可能性はP（Rain | Cloud）と書かれています

P（Rain | Cloud）= P（Rain）P（Cloud | Rain）/ P（Cloud）

P（Rain）は雨の確率= 10％です

P（Cloud | Rain）は、雨が発生した場合の雲の確率= 50％

P（クラウド）はクラウドの確率= 40％

P（雨|雲）= 0.1 x 0.5 / 0.4 = .125

したがって、12.5％の確率で雨が降ります。

アプリケーション

ベイズの定理のいくつかの応用が現実の世界に存在します。 定理のいくつかの主な用途は次のとおりです。

1.仮説のモデリング

ベイズの定理は、応用機械学習に幅広い応用を見出し、データとモデルの関係を確立します。 応用機械学習は、特定のデータセットでさまざまな仮説をテストおよび分析するプロセスを使用します。

データとモデルの関係を説明するために、ベイズの定理は確率モデルを提供します。

P（h | D）= P（D | h）* P（h）/ P（D）

どこ、

P（h | D）：仮説の事後確率

P（h）：仮説の事前確率。

P（D）が増加すると、P（h | D）が減少します。 逆に、P（h）と仮説が与えられたデータを観測する確率が増加すると、P（h | D）の確率が増加します。

2.分類のためのベイズの定理

分類の方法には、特定のデータのラベル付けが含まれます。 これは、データサンプルが与えられた場合のクラスラベルの条件付き確率の計算として定義できます。

P（クラス|データ）=（P（データ|クラス）* P（クラス））/ P（データ）

ここで、P（class | data）は、提供されたデータが与えられた場合のクラスの確率です。

計算はクラスごとに実行できます。 確率が最も高いクラスを入力データに割り当てることができます。

条件付き確率の計算は、少数の例の条件下では実行できません。 したがって、ベイズの定理を直接適用することはできません。 分類モデルの解決策は、単純化された計算にあります。

• 単純ベイズ分類器

ベイズの定理は、入力変数が他の変数に依存しているため、計算が複雑になると考えています。 したがって、仮定は削除され、すべての入力変数は独立変数と見なされます。 その結果、モデルは依存条件付き確率モデルから独立条件付き確率モデルに変わります。 最終的には複雑さが軽減されます。

ベイズの定理のこの単純化は、ナイーブベイズと呼ばれます。 これは、モデルの分類と予測に広く使用されています。

• ベイズ最適分類器

これは、トレーニングデータセットが与えられた場合の新しい例の予測を含む一種の確率モデルです。 Bayes Optimal Classifierの1つの例は、「トレーニングデータを前提として、新しいインスタンスの最も可能性の高い分類は何ですか？」です。

トレーニングデータが与えられた場合の新しいインスタンスの条件付き確率の計算は、次の式で実行できます。

P（vj | D）= sum {h in H} P（vj | hi）* P（hi | D）

vjが分類される新しいインスタンスである場合、

Hは、インスタンスを分類するための一連の仮説です。

こんにちはは与えられた仮説です、

P（vj | hi）は、仮説hiが与えられた場合のviの事後確率であり、

P（hi | D）は、データDが与えられた場合の仮説hiの事後確率です。

3.機械学習でのベイズの定理の使用

機械学習におけるベイズの定理の最も一般的なアプリケーションは、分類問題の開発です。 分類ではなく他のアプリケーションには、最適化とカジュアルモデルが含まれます。

• ベイズ最適化

特定の目的関数の最小または最大のコストをもたらす入力を見つけることは、常に困難な作業です。 ベイズ最適化はベイズの定理に基づいており、大域的最適化問題を検索するための側面を提供します。 この方法には、確率モデル（代理関数）の構築、取得関数の検索、および実際の目的関数を評価するための候補サンプルの選択が含まれます。

応用機械学習では、ベイズ最適化を使用して、パフォーマンスの高いモデルのハイパーパラメーターを調整します。

• ベイジアンビリーフネットワーク

変数間の関係は、確率モデルを使用して定義できます。 また、確率の計算にも使用されます。 完全な条件付き確率モデルでは、大量のデータが原因で確率を計算できない場合があります。 ナイーブベイズは、計算のアプローチを簡素化しました。 さらに別の方法が存在し、確率変数間の既知の条件付き依存性と他の場合の条件付き独立性に基づいてモデルが開発されます。 ベイジアンネットワークは、有向エッジを持つ確率的グラフモデルを通じて、この依存性と独立性を表示します。 既知の条件付き依存関係は有向エッジとして表示され、欠落している接続はモデルの条件付き独立性を表します。

4.ベイジアンスパムフィルタリング

スパムフィルタリングは、ベイズの定理のもう1つのアプリケーションです。 2つのイベントが存在します：

• イベントA：メッセージはスパムです。
• テストX：メッセージに特定の単語が含まれています（X）

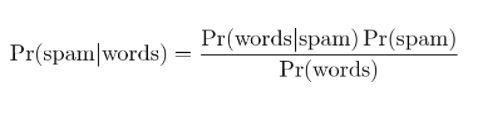
ベイズの定理を適用すると、「テスト結果」からメッセージがスパムであるかどうかを予測できます。 メッセージ内の単語を分析すると、スパムメッセージである可能性を計算できます。 メッセージが繰り返されるフィルターのトレーニングにより、メッセージに特定の単語が含まれる可能性がスパムになるという事実が更新されます。

例を用いたベイズの定理の適用

触媒メーカーは、特定の電極触媒（EC）の欠陥をテストするためのデバイスを製造しています。 触媒の生産者は、ECに欠陥がある場合は97％の信頼性があり、欠陥がない場合は99％の信頼性があると主張しています。 ただし、上記のECの4％は、納品時に欠陥があると予想される場合があります。 ベイズの定理は、デバイスの真の信頼性を確認するために適用されます。 基本的なイベントセットは

A：ECに欠陥があります。 A'：ECは完璧です。 B：ECに欠陥があることがテストされています。 B'：ECは完璧であることがテストされています。

確率は

B / A：ECは（欠陥があることがわかっている）欠陥があり、テスト済みで欠陥があります、P（B / A）= 0.97、

B'/ A：ECは（欠陥があることがわかっている）欠陥がありますが、完璧にテストされています、P（B' / A）= 1-P（B / A）= 0.03、

B / A'：ECは（あることがわかっている）欠陥がありますが、テスト済みの欠陥があります。P（B / A'）= 1- P（B' / A'）= 0.01

B'/ A：= ECは（既知である）完璧であり、テストされた完璧なP（B' / A'）= 0.99

ベイズの定理によって計算される確率は次のとおりです。

計算の確率は、完璧なECを拒否する可能性が高く（約20％）、欠陥のあるECを特定する可能性が低い（約80％）ことを示しています。

結論

ベイズの定理の最も顕著な特徴の1つは、いくつかの確率比から、膨大な量の情報を取得できることです。 尤度の手段を使用すると、前のイベントの確率を事後確率に変換できます。 ベイズの定理のアプローチは、統計学、認識論、および帰納論理の分野に適用できます。

ベイズの定理、AI、機械学習について詳しく知りたい場合は、IIIT-BとupGradの機械学習とAIのエグゼクティブPGプログラムをご覧ください。これは、働く専門家向けに設計されており、450時間以上の厳格なトレーニング、30時間以上のケースを提供します。研究と課題、IIIT-B卒業生のステータス、5つ以上の実践的なキャップストーンプロジェクト、トップ企業との仕事の支援。