Cos'è il pensiero bayesiano? Introduzione e teorema

Un teorema statistico fornito dallo statistico e filosofo inglese Thomas Bayes nel 1700 continua a essere una luce guida per scienziati e analisti di tutto il mondo. Oggi, il pensiero bayesiano trova applicazione in medicina, scienza, tecnologia e molte altre discipline e continua a influenzare fortemente la nostra visione del mondo e le azioni che ne derivano.

L'idea di Thomas Bayes era sorprendentemente semplice. Secondo Bayes, la probabilità che un'ipotesi sia vera dipende da due condizioni: quanto sia ragionevole basata su ciò che già sappiamo (la conoscenza precedente) e quanto bene si adatta a nuove prove. Pertanto, il pensiero bayesiano differisce dal tradizionale test di ipotesi in quanto il primo include la conoscenza precedente prima di saltare alle conclusioni.

Con l'introduzione preliminare in mente, tuffiamoci un po' più nel dettaglio delle statistiche bayesiane.

Statistica bayesiana

In parole povere, le statistiche bayesiane applicano le probabilità ai problemi statistici per aggiornare le credenze precedenti alla luce dell'evidenza di nuovi dati. La probabilità esprime un grado di fiducia in un evento specifico.

Il grado di convinzione può essere basato su conoscenze precedenti sull'evento basate su ipotesi personali o risultati di esperimenti precedenti. La statistica bayesiana utilizza il teorema di Bayes per calcolare le probabilità. Il teorema di Bayes, a sua volta, descrive la probabilità condizionata di un evento sulla base di nuove prove e informazioni precedenti relative all'evento.

Con questo in mente, rispolveriamo il concetto fondamentale di probabilità condizionata prima di comprendere a fondo il teorema di Bayes.

Probabilità condizionale

La probabilità condizionata può essere definita come la probabilità di un evento o di un risultato in base al verificarsi di un evento o un risultato precedente. Si calcola moltiplicando la probabilità dell'evento precedente per la probabilità dell'evento successivo o condizionale.

Diamo un'occhiata ad un esempio per capire meglio il concetto .

• L'evento A è che una famiglia che pianifica un'uscita andrà a fare un picnic. C'è una probabilità dell'80% che la famiglia vada al picnic.
• L'evento B è che pioverà il giorno in cui la famiglia andrà a fare un picnic. Le previsioni del tempo dicono che c'è una probabilità del 60% di precipitazioni nel giorno del picnic.
• Quindi, la probabilità (P) che la famiglia vada al picnic e piova è calcolata come segue:

P (Picnic e pioggia) = P (Pioggia | Picnic) P (Picnic) = (0,60) * (0,80) = 0,48

Nell'esempio sopra, la probabilità condizionata considera i due eventi A e B in relazione tra loro, cioè la probabilità che la famiglia vada al picnic e piova anche lo stesso giorno.

Quindi, la probabilità condizionata differisce dalla probabilità incondizionata perché quest'ultima si riferisce alla probabilità che si verifichi un evento indipendentemente dal fatto che si siano verificati altri eventi o eventi o siano presenti altre condizioni.

La formula per la probabilità condizionata

La formula per la probabilità condizionata deriva dalla regola della moltiplicazione delle probabilità:

P (A e B) o P (AUB) = P ( B dato A) o P (B | A) * P (A)

Nell'equazione precedente, P (A e B) è la probabilità congiunta, riferita alla probabilità che due o più eventi si verifichino contemporaneamente. Si scrive anche come P (A,B).

Ecco come dedurre l'equazione di probabilità condizionale dalla regola di moltiplicazione:

Passaggio 1: annota la regola di moltiplicazione.

P (LA e B) = P (B | LA) * P (LA)

Passaggio 2: dividere entrambi i lati dell'equazione per P (A).

P (LA e B) / P (LA) = P (B | LA) * P (LA) / P (LA)

Passaggio 3: annullare P (A) sul lato destro dell'equazione.

P (LA e B) / P (LA) = P (B | LA)

Passaggio 4: riscrivi l'equazione.

P (LA e B) = P (B | LA) / P (LA)

Pertanto, la formula per la probabilità condizionata è data come:

P (LA e B) = P (B | LA) / P (LA)

Teorema di Bayes

Usando il teorema di Bayes, possiamo aggiornare le nostre convinzioni e convinzioni sulla base di nuove e rilevanti prove. Ad esempio, se stiamo cercando di capire la probabilità che una determinata persona abbia il cancro, generalmente assumiamo che sia la percentuale della popolazione che ha il cancro. Tuttavia, se introduciamo ulteriori prove, ad esempio che la persona in questione è un fumatore abituale, possiamo aggiornare la nostra percezione (e quindi la probabilità) poiché la probabilità di avere il cancro è maggiore se un individuo è un fumatore. Pertanto, utilizziamo sia le nostre conoscenze precedenti che le prove aggiuntive per migliorare le nostre stime.

La formula per il teorema di Bayes

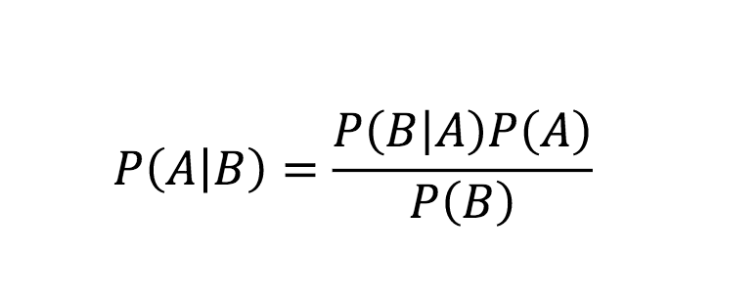
Fonte

L'equazione di cui sopra è la regola di Bayes. Ora, esaminiamo la derivazione graduale dell'equazione del teorema di Bayes.

Passaggio 1: considera due eventi, A e B. A è l'evento di cui vogliamo calcolare la probabilità e B è l'evidenza aggiuntiva correlata ad A.

Passaggio 2: annotare la relazione tra la probabilità congiunta e la probabilità condizionata degli eventi A e B.

P (LA, B) = P (LA | B) * P (B) = P (B, LA) = P (B | LA) * P (LA)

Passaggio 3: imposta i due termini di probabilità condizionali uguali tra loro.

P(LA | B) * P(B) = P (B | A) * P(A)

Passaggio 4: dividere entrambi i lati dell'equazione per P (B).

P (LA | B) * P (B) / P (B) = P (B | A) * P (LA) / P (B)

Passaggio 5: annullare P (B) sul lato sinistro dell'equazione.

P (LA | B) = P (B | LA) * P (LA) / P (B)

Quindi, otteniamo la formula del teorema di Bayes come segue:

P (LA | B) = P (B | LA) * P (LA) / P (B)

Comprensione dei termini nell'equazione del teorema di Bayes

P (LA | B) = P (B | LA) * P (LA) / P (B)

• P (A | B) è chiamata probabilità a posteriori o probabilità che stiamo cercando di stimare. Sulla base dell'esempio precedente, la probabilità a posteriori sarebbe la probabilità che la persona abbia il cancro, dato che la persona è un fumatore abituale.
• P (B | A) è chiamata verosimiglianza , riferendosi alla probabilità di rilevare l'evidenza aggiuntiva, data la nostra ipotesi iniziale. Nell'esempio sopra, la probabilità è la probabilità che la persona sia un fumatore, dato che la persona ha il cancro.
• P (A) è la probabilità a priori o la probabilità della nostra ipotesi senza alcuna prova o informazione aggiuntiva. Nell'esempio sopra, la probabilità a priori è la probabilità di avere il cancro.
• P (B) è la probabilità marginale o la probabilità totale di osservare l'evidenza. Nel contesto dell'esempio precedente, la probabilità marginale è la probabilità di essere un fumatore.

Un semplice esempio per comprendere il teorema di Bayes

Utilizzando alcuni numeri ipotetici nell'esempio precedente, vedremo l'effetto dell'applicazione del teorema di Bayes.

Supponiamo che la probabilità di avere il cancro sia 0,06, cioè il 6% delle persone abbia il cancro. Ora, supponiamo che la probabilità di essere un fumatore sia 0,20 o il 20% delle persone sono fumatori e il 30% delle persone con cancro sono fumatori. Quindi, P (Fumatore | Cancro) = 0,30.

Inizialmente, la probabilità di avere il cancro è semplicemente 0,06 (precedente). Ma usando la nuova prova, possiamo calcolare P (Cancro | Fumatore) = P ((Fumatore | Cancro) * P (Cancro)) / P (Fumatore) = (0,30*0,06) / (0,20) = 0,09.

Impara i corsi di scienza dei dati online dalle migliori università del mondo. Guadagna programmi Executive PG, programmi di certificazione avanzati o programmi di master per accelerare la tua carriera.

Via da seguire: padroneggia i concetti di statistica per una carriera nella scienza dei dati o nell'apprendimento automatico

La piattaforma di apprendimento EdTech superiore di upGrad ha avuto un impatto su oltre 500.000 professionisti che lavorano in tutto il mondo con la sua pletora di corsi ed esperienze di apprendimento coinvolgenti. Con una base di oltre 40.000 studenti sparsi in oltre 85 paesi, i corsi rilevanti per il settore di upGrad sono garantiti per far avanzare la tua carriera nel tuo campo di scelta.

Il Master of Science in Data Science è un corso di 18 mesi che impartisce competenze chiave in statistica, analisi predittiva, machine learning, analisi dei big data, visualizzazione dei dati, ecc.

Punti salienti del programma:

• Master presso la Liverpool John Moores University e Executive PGP presso IIIT Bangalore
• Oltre 500 ore di contenuti, oltre 60 casi di studio e progetti, oltre 20 sessioni dal vivo, oltre 14 linguaggi di programmazione e strumenti
• Reti di settore, sessioni di risoluzione dei dubbi e supporto all'apprendimento

Advanced Certificate Program in Machine Learning e Deep Learning è un corso rigoroso di 6 mesi con opportunità di networking tra pari, progetti pratici, tutoraggio del settore e assistenza professionale a 360 gradi.

Punti salienti del programma:

• Prestigioso riconoscimento da IIIT Bangalore
• Oltre 240 ore di contenuti, oltre 5 casi di studio e progetti, oltre 24 sessioni dal vivo, copertura di 12 linguaggi di programmazione, strumenti e librerie
• Sessioni di coaching di gruppo 1:8 e sessioni di tutoraggio 1:1 con esperti del settore

Conclusione

Il pensiero bayesiano è alla base di diverse aree del pensiero, dell'indagine e delle credenze umane, anche se la maggior parte di noi non ne è consapevole. Dallo screening del cancro e dal riscaldamento globale alla politica monetaria, alla valutazione del rischio e all'assicurazione , il pensiero bayesiano è fondamentale. Si ritiene che anche il famoso matematico britannico Alan Turing abbia utilizzato l'approccio bayesiano per decifrare il Codice Enigma tedesco durante la seconda guerra mondiale.

Iscriviti a upGrad e approfondisci la tua conoscenza dei concetti statistici chiave e altro ancora!