Guida introduttiva alla regressione binomiale negativa: guida passo passo

La tecnica della Regressione Binomiale Negativa viene utilizzata per eseguire la modellazione delle variabili di conteggio. Il metodo è quasi simile al metodo di regressione multipla. Tuttavia, c'è la differenza che nel caso della regressione binomiale negativa, la variabile dipendente, cioè Y, segue la distribuzione binomiale negativa. Pertanto, i valori della variabile possono essere interi non negativi come 0, 1, 2.

Il metodo è anche un'estensione della regressione di Poisson che fa un rilassamento nell'assumere che la media sia uguale alla varianza. Uno dei modelli tradizionali di regressione binomiale, definito come “NB2”, si basa sulla distribuzione mista di Poisson-gamma.

Il metodo della regressione di Poisson viene generalizzato mediante l'aggiunta di una variabile di rumore gamma. Questa variabile ha un valore medio uno e anche un parametro di scala che è "v".

Ecco alcuni esempi di regressione binomiale negativa:

• I dirigenti scolastici hanno condotto uno studio per studiare il comportamento di frequenza degli studenti delle scuole superiori di due scuole. I fattori che potrebbero influenzare il comportamento di frequenza potrebbero includere i giorni in cui i ragazzi erano assenti da scuola. Inoltre, il programma a cui erano iscritti.
• Un ricercatore di uno studio relativo alla salute ha condotto uno studio su quanti anziani hanno visitato un ospedale negli ultimi 12 mesi. Lo studio si è basato sulle caratteristiche dell'individuo e sui piani sanitari acquistati dagli anziani.

Esempio di regressione binomiale negativa

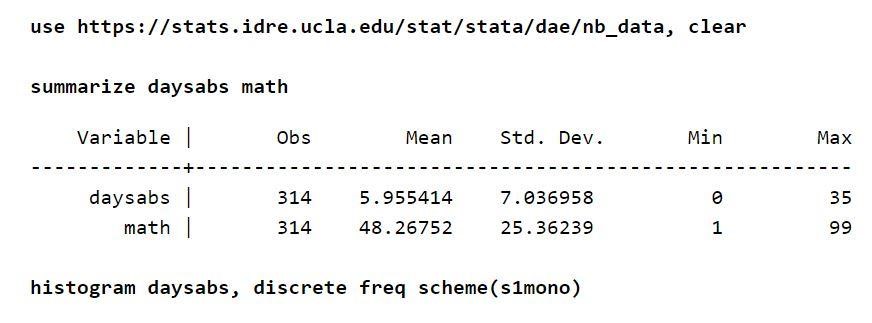
Supponiamo che ci sia un foglio presenze di circa 314 studenti delle scuole superiori. I dati vengono prelevati da due scuole urbane e archiviati in un file denominato nb_data.dta. La variabile di risposta interessante in questo esempio sono i giorni assenti che sono "daysabs". È presente una variabile, "math", che definisce il punteggio di matematica per ogni studente. C'è un'altra variabile che è "prog". Questa variabile indica il programma a cui sono iscritti gli studenti.

Fonte

Ciascuna delle variabili ha circa 314 osservazioni. Pertanto, anche le distribuzioni tra le variabili sono ragionevoli. Inoltre, considerando la variabile di risultato, la media incondizionata è inferiore alla varianza.

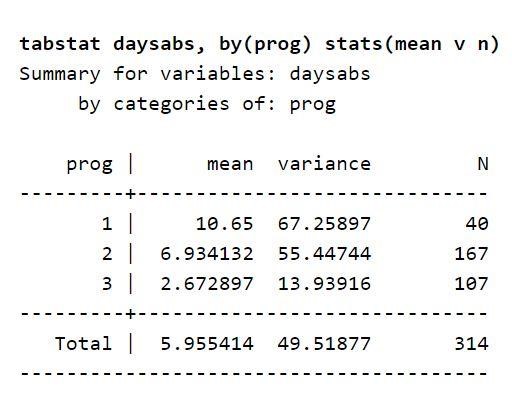
Ora, concentrati sulla descrizione della variabile considerata nel set di dati. Una tabella elenca i giorni medi di assenza da scuola di uno studente in ogni tipo di programma. Ciò suggerisce che il programma di tipo variabile può prevedere i giorni in cui lo studente era assente da scuola. Puoi anche usarlo per prevedere la variabile di risultato. Questo perché il valore medio per la variabile di risultato varia in base alla variabile prog. Inoltre, i valori delle varianze sono superiori a quelli di ciascun livello della variabile prog. Questi valori sono chiamati varianze e medie. Le differenze esistenti suggeriscono che vi sia la presenza di una dispersione eccessiva, e quindi sarà opportuno utilizzare un modello binomiale negativo.

Fonte

Un ricercatore può prendere in considerazione diversi metodi di analisi per questo tipo di studio. Questi metodi sono descritti di seguito. Alcuni dei metodi di analisi che l'utente può utilizzare per analizzare il modello di regressione sono:

1. Regressione binomiale negativa

Il metodo della regressione binomiale negativa deve essere utilizzato in presenza di dati sovradispersi. Ciò significa che il valore della varianza condizionale è maggiore o supera il valore della media condizionale. Il metodo è considerato generalizzato dal metodo di regressione di Poisson. Questo perché entrambi i metodi hanno la stessa struttura della media. Ma c'è un parametro aggiuntivo nella regressione binomiale negativa utilizzata per modellare la dispersione eccessiva. Gli intervalli di confidenza sono considerati più stretti della regressione della passione quando la distribuzione condizionale è eccessivamente dispersa dalla variabile di risultato.

2. Regressione di Poisson

Il metodo della regressione di Poisson viene utilizzato nella modellazione dei dati di conteggio. Molte estensioni possono essere utilizzate per modellare le variabili di conteggio nella regressione di Poisson.

3. Regressione OLS

I risultati delle variabili di conteggio vengono talvolta trasformati in log e quindi analizzati attraverso il metodo della regressione OLS. Tuttavia, a volte ci sono problemi relativi al metodo di regressione OLS. Questi problemi potrebbero essere la perdita di dati dovuta alla generazione di qualsiasi valore indefinito attraverso la considerazione del log del valore zero. Inoltre, potrebbe essere generato a causa della mancanza di modellazione dei dati dispersi.

4. Modelli a gonfiaggio zero

Questi tipi di modelli cercano di tenere conto di tutti gli zeri in eccesso nel modello.

Analisi utilizzando la regressione binomiale negativa

Il comando “nbreg” è usato per stimare il modello di Regressione Binomiale Negativa. C'è una "i" prima della variabile "prog". La presenza della “i” indica che la variabile è di tipo factor, cioè variabile categoriale. Questi dovrebbero essere inclusi come variabili indicatore nel modello.

• L'output del modello inizia con un log di iterazione. Si parte attraverso il fitting del modello di Poisson, seguito da un modello nullo, e poi dal modello del binomio negativo. Il metodo utilizza la stima della massima verosimiglianza e continua a iterare fino a quando non si verifica una modifica nel valore del log finale. La verosimiglianza del log viene utilizzata per il confronto dei modelli.
• Le informazioni successive sono nel file di intestazione.
• Ci sono le informazioni sui coefficienti della regressione binomiale negativa appena sotto l'intestazione. I coefficienti vengono generati per ogni variabile insieme agli errori come i valori p, i punteggi z. C'è anche un intervallo di confidenza del 95% per tutti i coefficienti. Il coefficiente per la variabile "matematica" è -0,006, che denota che è statisticamente significativa. Il risultato significa che se c'è un aumento di un'unità sulla variabile "matematica", il conteggio log atteso per il numero di giorni assente diminuisce di un valore di 0,006. Inoltre, il valore della 2. prog, la variabile indicatore, è la differenza attesa nel conteggio dei log tra i due gruppi (gruppo 2 e gruppo di riferimento).
• La stima del parametro per la sovradispersione trasferita logaritmica viene eseguita e quindi visualizzata con il valore non trasformato. Nel modello di Poisson, il valore è zero.
• C'è un'informazione sulla probabilità del test del rapporto sotto la tabella dei coefficienti. Il modello può essere ulteriormente compreso attraverso l'uso dei comandi "margini".

Processo di analisi della regressione binomiale negativa in Python

I pacchetti richiesti per eseguire il processo di regressione devono essere importati da Python. Questi pacchetti sono elencati di seguito:

• import statsmodels.api come sm
• importa matplotlib.pyplot come plt
• importa numpy come np
• da patsy import dmatrices
• importa panda come pd

Considerazioni sulla regressione binomiale negativa

Ci sono alcune cose che dovrebbero essere considerate durante l'applicazione del metodo dell'analisi della regressione binomiale negativa. Questi includono:

• Se c'è la presenza di piccoli campioni, il metodo di regressione binomiale negativa non è raccomandato.
• A volte sono presenti zeri in eccesso che potrebbero essere una causa della dispersione eccessiva. Questi zeri potrebbero essere generati a causa del processo di aggiunta della generazione dei dati. Se si verifica un caso del genere, si consiglia di utilizzare il metodo del modello a gonfiaggio zero.
• Se il processo di generazione dei dati non considera gli zeri, in questi casi si consiglia di utilizzare il metodo del modello troncato zero.
• Esiste una variabile di esposizione associata ai dati di conteggio. La variabile indica le volte in cui esiste la possibilità che l'evento possa verificarsi. Questa variabile è necessaria per essere incorporata nel modello di regressione binomiale negativa. Questo viene fatto attraverso l'opzione di exp().
• La variabile di risultato non può essere alcun valore negativo nel modello dell'analisi di regressione binomiale negativa. Inoltre, la variabile di esposizione non può avere il valore 0.
• Il comando “glm” può essere utilizzato anche per eseguire un metodo di analisi di regressione binomiale negativa. Questo può essere fatto attraverso il collegamento del log e anche la famiglia di binomi.
• Per ottenere i residui è necessario il comando “glm”. Questo per verificare se ci sono altre ipotesi nel modello di regressione binomiale negativa.
• C'è l'esistenza delle varie misure dello pseudo-R-quadrato. Tuttavia, ogni misura fornisce informazioni simili a quelle fornite dall'R-quadrato nella regressione di OLS.

Conclusione

L'articolo ha discusso l'argomento della regressione binomiale negativa . Abbiamo visto che è quasi simile al metodo delle regressioni multiple ed è una forma generalizzata della distribuzione di Poisson. Ci sono diverse applicazioni del metodo. La tecnica può essere applicata anche attraverso il linguaggio di programmazione Python o in R.

Sono presenti anche diversi casi di studio che ne mostrano l'applicazione in studi come l'invecchiamento. Inoltre, i modelli classici di regressione che possono essere utilizzati sui dati di conteggio sono la regressione di Poisson, la regressione binomiale negativa e la regressione geometrica. Questi metodi appartenevano alla famiglia dei modelli lineari e sono stati inclusi in quasi tutti i pacchetti statistici come il sistema R.

Se vuoi eccellere nel machine learning e vuoi esplorare il campo dei dati, puoi controllare il corso Executive PG Program in Machine Learning & AI offerto da upGrad. Quindi, se sei un professionista che sogna di essere un esperto di machine learning, vieni a fare l'esperienza di ottenere una formazione con esperti. Maggiori dettagli possono essere raggiunti attraverso il nostro sito web. Per qualsiasi domanda, il nostro team può assisterti tempestivamente.

Migliora la tua carriera nell'apprendimento automatico e nell'intelligenza artificiale

Richiedi ora la certificazione esecutiva in Ai-ml da IIITB