Impara l'algoritmo di Naive Bayes per l'apprendimento automatico [con esempi]
Pubblicato: 2021-02-25Sommario
introduzione
In matematica e programmazione, alcune delle soluzioni più semplici sono solitamente le più potenti. L'ingenuo algoritmo di Bayes è un classico esempio di questa affermazione. Anche con il forte e rapido avanzamento e sviluppo nel campo dell'apprendimento automatico, questo algoritmo Naive Bayes è ancora forte come uno degli algoritmi più utilizzati ed efficienti. L'ingenuo algoritmo di Bayes trova le sue applicazioni in una varietà di problemi, inclusi i compiti di classificazione ei problemi di elaborazione del linguaggio naturale (NLP).
L'ipotesi matematica del teorema di Bayes funge da concetto fondamentale alla base di questo algoritmo Naive Bayes. In questo articolo, esamineremo le basi del teorema di Bayes, l'algoritmo Naive Bayes insieme alla sua implementazione in Python con un problema di esempio in tempo reale. Insieme a questi, esamineremo anche alcuni vantaggi e svantaggi dell'algoritmo Naive Bayes rispetto ai suoi concorrenti.
Nozioni di base sulla probabilità
Prima di avventurarci nella comprensione del teorema di Bayes e dell'algoritmo di Bayes ingenuo, rispolveriamo le nostre conoscenze esistenti sui fondamenti della probabilità.
Come tutti sappiamo per definizione, dato un evento A, la probabilità che tale evento si verifichi è data da P(A). Con probabilità, due eventi A e B sono definiti come eventi indipendenti se il verificarsi dell'evento A non altera la probabilità di accadimento dell'evento B e viceversa. D'altra parte, se l'occorrenza di una persona cambia la probabilità dell'altra, vengono definiti eventi dipendenti.
Veniamo introdotti a un nuovo termine chiamato Probabilità Condizionata . In matematica, la Probabilità Condizionata per due eventi A e B data da P (A| B) è definita come la probabilità che si verifichi l'evento A dato che l'evento B si è già verificato. A seconda della relazione tra i due eventi A e B se sono dipendenti o indipendenti, la Probabilità Condizionata viene calcolata in due modi.
- La probabilità condizionata di due eventi dipendenti A e B è data da P (A| B) = P (A e B) / P (B)
- L'espressione per la probabilità condizionata di due eventi indipendenti A e B è data da, P (A| B) = P (A)
Conoscendo la matematica alla base della probabilità e delle probabilità condizionali, passiamo ora al teorema di Bayes.

Teorema di Bayes
In statistica e teoria della probabilità, il teorema di Bayes noto anche come regola di Bayes viene utilizzato per determinare la probabilità condizionata degli eventi. In altre parole, il teorema di Bayes descrive la probabilità di un evento basata sulla conoscenza preliminare delle condizioni che potrebbero essere rilevanti per l'evento.
Per capirlo in modo più semplice, considera che dobbiamo sapere che la probabilità che il prezzo di una casa sia molto alta. Se conosciamo gli altri parametri come la presenza di scuole, officine mediche e ospedali nelle vicinanze, allora possiamo fare una valutazione più accurata degli stessi. Questo è esattamente ciò che esegue il teorema di Bayes.
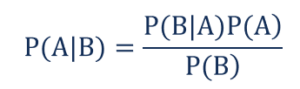
tale che,
- P(A|B) – la probabilità condizionata che si verifichi l'evento A, dato che l'evento B si è verificato anche noto come Probabilità Posteriore .
- P(B|A) – la probabilità condizionata che si verifichi l'evento B, dato che si è verificato l'evento A noto anche come Probabilità di Probabilità .
- P(A) – la probabilità che si verifichi l'evento A, nota anche come Probabilità Prior.
- P(B) – la probabilità che si verifichi l'evento B, nota anche come Probabilità marginale.
Supponiamo di avere un semplice problema di Machine Learning con 'n' variabili indipendenti e la variabile dipendente che è l'output è un valore booleano (Vero o Falso). Supponiamo che gli attributi indipendenti siano di natura categoriale, consideriamo 2 categorie per questo esempio. Quindi, con questi dati, dobbiamo calcolare il valore della Probabilità di Probabilità, P(B|A).
Quindi, osservando quanto sopra, scopriamo che dobbiamo calcolare 2*(2^ n -1 ) parametri per apprendere questo modello di Machine Learning. Allo stesso modo, se abbiamo 30 attributi booleani indipendenti, il numero totale di parametri da calcolare sarà vicino a 3 miliardi, un costo computazionale estremamente elevato.
Questa difficoltà nella costruzione di un modello di Machine Learning con il teorema di Bayes ha portato alla nascita e allo sviluppo dell'algoritmo Naive Bayes.
Algoritmo di Bayes ingenuo
Per essere pratico, la suddetta complessità del teorema di Bayes deve essere ridotta. Ciò si ottiene esattamente nell'algoritmo di Naive Bayes facendo poche ipotesi. Le ipotesi fatte sono che ciascuna caratteristica dia un contributo indipendente e uguale al risultato.
L'ingenuo algoritmo di Bayes è un algoritmo di apprendimento supervisionato e si basa sul teorema di Bayes che viene utilizzato principalmente per risolvere problemi di classificazione. È uno dei classificatori più semplici e accurati che costruisce modelli di Machine Learning per fare previsioni rapide. Matematicamente, è un classificatore probabilistico in quanto effettua previsioni utilizzando la funzione di probabilità degli eventi.
Esempio di problema
Per comprendere la logica dietro le ipotesi, esaminiamo un semplice set di dati per ottenere una migliore intuizione.
| Colore | Tipo | Origine | Furto? |
| Nero | Berlina | Importato | sì |
| Nero | SUV | Importato | No |
| Nero | Berlina | Domestico | sì |
| Nero | Berlina | Importato | No |
| Marrone | SUV | Domestico | sì |
| Marrone | SUV | Domestico | No |
| Marrone | Berlina | Importato | No |
| Marrone | SUV | Importato | sì |
| Marrone | Berlina | Domestico | No |
Dal set di dati sopra indicato, possiamo derivare i concetti delle due ipotesi che abbiamo definito per l'algoritmo di Naive Bayes sopra.
- Il primo presupposto è che tutte le caratteristiche siano indipendenti l'una dall'altra. Qui vediamo che ogni attributo è indipendente, ad esempio il colore "Rosso" è indipendente dal Tipo e dall'Origine dell'auto.
- Successivamente, a ciascuna caratteristica deve essere data uguale importanza. Allo stesso modo, la sola conoscenza del tipo e dell'origine dell'auto non è sufficiente per prevedere l'output del problema. Quindi, nessuna delle variabili è irrilevante e quindi tutte danno un uguale contributo al risultato.
Per riassumere, A e B sono condizionatamente indipendenti dato C se e solo se, data la conoscenza che C si verifica, la conoscenza se A si verifica non fornisce informazioni sulla probabilità che B si verifichi e la conoscenza se B si verifica non fornisce informazioni su la probabilità che si verifichi A. Queste ipotesi rendono l'algoritmo di Bayes – Naive . Da qui il nome, Algoritmo Naive Bayes.
Quindi per il problema sopra indicato, il Teorema di Bayes può essere riscritto come:
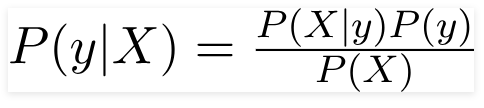
tale che,
- Il vettore delle caratteristiche indipendenti, X = (x 1 , x 2 , x 3 ……x n ) che rappresenta le caratteristiche come Colore, Tipo e Origine dell'Automobile.
- La variabile di output, y ha solo due risultati Sì o No.
Quindi, sostituendo i valori sopra, otteniamo la formula di Naive Bayes come,
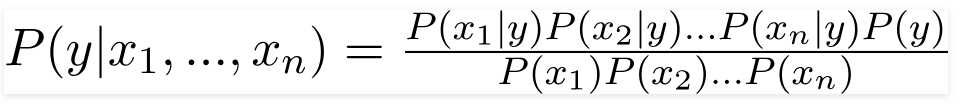
Per calcolare la probabilità a posteriori P(y|X), dobbiamo creare una tabella di frequenza per ogni attributo rispetto all'output. Quindi convertiamo le tabelle di frequenza in tabelle di verosimiglianza, dopodiché utilizziamo infine l'equazione bayesiana ingenua per calcolare la probabilità a posteriori per ciascuna classe. Come risultato della previsione viene scelta la classe con la probabilità a posteriori più alta. Di seguito sono riportate le tabelle di frequenza e probabilità per tutti e tre i predittori.
Tabella di frequenza dei colori Tabella di probabilità dei colori
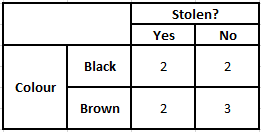
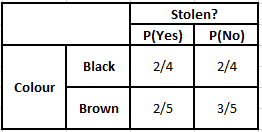
Tabella di frequenza del tipo Tabella di probabilità del tipo

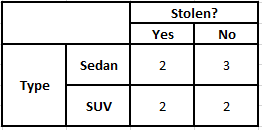
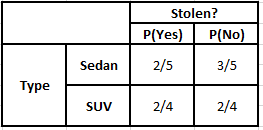
Tabella di frequenza dell'origine Tabella di probabilità dell'origine
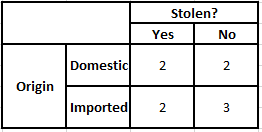
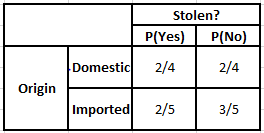
Considera il caso in cui abbiamo bisogno di calcolare le probabilità a posteriori per le condizioni indicate di seguito:
| Colore | Tipo | Origine |
| Marrone | SUV | Importato |
Pertanto, dalla formula sopra indicata, possiamo calcolare le probabilità posteriori come mostrato di seguito:
P(Sì | X) = P(Marrone | Sì) * P(SUV | Sì) * P(Importato | Sì) * P(Sì)
= 2/5 * 2/4 * 2/5 * 1
= 0,08
P(No | X) = P(Marrone | No) * P(SUV | No) * P(Importato | No) * P(No)
= 3/5 * 2/4 * 3/5 * 1
= 0,18
Dai valori sopra calcolati, poiché le Probabilità Posteriori per No è Maggiore di Sì (0,18>0,08), si può dedurre che un'auto di Colore Marrone, Tipo SUV di Origine Importata è classificata come “No”. Quindi, l'auto non viene rubata.
Implementazione in Python
Ora che abbiamo compreso la matematica dietro l'algoritmo Naive Bayes e lo abbiamo anche visualizzato con un esempio, esaminiamo il suo codice di Machine Learning in linguaggio Python.
Correlati: classificatore ingenuo di Bayes
Analisi del problema
Per implementare il programma di classificazione Naive Bayes in Machine Learning utilizzando Python, utilizzeremo il famosissimo "Iris Flower Dataset". Il set di dati del fiore dell'iride o set di dati dell'iride di Fisher è un set di dati multivariato introdotto dallo statistico, eugenista e biologo britannico Ronald Fisher nel 1998. Si tratta di un set di dati molto piccolo e di base che consiste in dati molto meno numerici contenenti informazioni su 3 classi di fiori appartenenti alla specie Iris che sono –
- Iris Setosa
- Iris Versicolore
- Iris Virginia
Ci sono 50 campioni di ciascuna delle tre specie per un totale di 150 righe. I 4 attributi (o) variabili indipendenti utilizzati in questo set di dati sono:
- lunghezza del sepalo in cm
- larghezza sepalo in cm
- lunghezza petalo in cm
- larghezza petalo in cm
La variabile dipendente è la “ specie ” del fiore che è identificata dai quattro attributi sopra indicati.
Passaggio 1: importare le librerie
Come sempre, il passaggio principale nella creazione di qualsiasi modello di Machine Learning sarà importare le librerie pertinenti. Per questo, caricheremo le librerie NumPy, Mathplotlib e Pandas per la pre-elaborazione dei dati.
importa numpy come np
importa matplotlib.pyplot come plt
importa panda come pd
Passaggio 2: caricamento del set di dati
Il set di dati del fiore di iris da utilizzare per l'addestramento del classificatore Naive Bayes deve essere caricato in un Pandas DataFrame. Le 4 variabili indipendenti devono essere assegnate alla variabile X e la variabile delle specie di output finale è assegnata a y.
dataset = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = dataset.iloc[:,:4].values
y = dataset['specie'].valuesdataset.head(5)>>
sepal_length sepal_width lunghezza_petalo larghezza_petalo specie
5,1 3,5 1,4 0,2 setosa
4,9 3,0 1,4 0,2 setosa
4,7 3,2 1,3 0,2 setosa
4,6 3,1 1,5 0,2 setosa
5,0 3,6 1,4 0,2 setosa
Passaggio 3: suddividere il set di dati nel set di allenamento e nel set di test
Dopo aver caricato il set di dati e le variabili, il passaggio successivo consiste nel preparare le variabili che verranno sottoposte al processo di addestramento. In questo passaggio, dobbiamo dividere le variabili X e y in training e nei set di dati di test. Per questo, assegneremo l'80% dei dati in modo casuale al set di addestramento che verrà utilizzato per scopi di addestramento e il restante 20% dei dati come set di test su cui verrà testato l'accuratezza del classificatore Naive Bayes addestrato.
da sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Passaggio 4: ridimensionamento delle funzionalità
Sebbene questo sia un processo aggiuntivo a questo piccolo set di dati, lo aggiungo per utilizzarlo in un set di dati più ampio. In questo, i dati nei set di addestramento e test vengono ridimensionati a un intervallo di valori compreso tra 0 e 1. Ciò riduce il costo di calcolo.
da sklearn.preprocessing import StandardScaler
sc = StandardScaler()
X_treno = sc.fit_transform(X_treno)
X_test = sc.transform(X_test)
Fase 5 – Addestrare il modello di classificazione Naive Bayes sul Training Set
È in questo passaggio che importiamo la classe Naive Bayes dalla libreria sklearn. Per questo modello utilizziamo il modello gaussiano, ci sono molti altri modelli come Bernoulli, Categorico e Multinomiale. Pertanto, X_train e y_train vengono adattati alla variabile del classificatore a scopo di addestramento.
da sklearn.naive_bayes importa GaussianNB
classificatore = GaussianNB()
classificatore.fit(X_treno, y_treno)
Passaggio 6 – Prevedere i risultati del set di test –
Prevediamo la classe della specie per il set di test utilizzando il modello addestrato e la confrontiamo con i valori reali della classe della specie.
y_pred = classificatore.predict(X_test)
df = pd.DataFrame({'Valori reali':y_test, 'Valori previsti':y_pred})
df>>
Valori reali Valori previsti
setosa setosa
setosa setosa
virginica virginica
versicolor versicolor
setosa setosa
setosa setosa
… … … … …
virginica versicolor
virginica virginica
setosa setosa
setosa setosa
versicolor versicolor
versicolor versicolor
Nel confronto di cui sopra, vediamo che c'è una previsione errata che ha previsto Versicolor invece di virginica.
Passaggio 7: matrice di confusione e precisione
Poiché abbiamo a che fare con la classificazione, il modo migliore per valutare il nostro modello di classificazione è stampare la matrice di confusione insieme alla sua accuratezza sul set di test.
da sklearn.metrics import confusion_matrix
cm = confusion_matrix(y_test, y_pred) da sklearn.metrics import precision_score

print ("Accuracy : ", precision_score(y_test, y_pred))
cm>>Precisione: 0,966666666666666667
>>array([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
Conclusione
Pertanto, in questo articolo, abbiamo esaminato le basi dell'algoritmo Naive Bayes, compreso la matematica alla base della classificazione insieme a un esempio risolto a mano. Infine, abbiamo implementato un codice di Machine Learning per risolvere un set di dati popolare utilizzando l'algoritmo di classificazione Naive Bayes.
Se sei interessato a saperne di più sull'IA e sull'apprendimento automatico, dai un'occhiata al Diploma PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, Status di Alumni IIIT-B, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.
In che modo la probabilità è utile in Machine Learning?
Potremmo dover prendere decisioni basate su informazioni parziali o incomplete in scenari del mondo reale. La probabilità ci aiuta a quantificare le incertezze in tali sistemi e gestire il rischio per l'attività. Il metodo tradizionale funziona solo per i risultati deterministici per azioni specifiche, ma c'è sempre un certo margine di incertezza in qualsiasi modello di previsione. Questa incertezza può derivare da molti parametri dei dati di input, come il rumore nei dati. Inoltre, le viste bayesiane dai teoremi di probabilità possono aiutare il riconoscimento del modello dai dati di input. Per questo, la probabilità utilizza il concetto di stima di massima verosimiglianza e quindi è utile per produrre risultati rilevanti.
A cosa serve la matrice di confusione?
La matrice di confusione è una matrice 2x2 utilizzata per interpretare le prestazioni del modello di classificazione. I valori veri per i dati di input devono essere noti affinché funzioni, quindi non possono essere rappresentati per dati senza etichetta. È costituito dal numero di falsi positivi (FP), veri positivi (TP), falsi negativi (FN) e veri negativi (TN). Le previsioni sono classificate in queste classi utilizzando il conteggio del training set e del test set. Ci aiuta a visualizzare parametri utili come accuratezza, precisione, richiamo e specificità. È relativamente facile da capire e ti dà un'idea chiara dell'algoritmo.
Quali sono i diversi tipi di modello Naive Bayes?
Tutti i tipi sono basati principalmente sul teorema di Bayes. Il modello Naive Bayes ha generalmente tre tipi: Gaussiano, Bernoulli e Multinomiale. Il Gaussian Naive Bayes aiuta con valori continui dai parametri di input e presuppone che tutte le classi di dati di input siano distribuite uniformemente. L'ingenuo Bayes di Bernoulli è un modello basato su eventi in cui le caratteristiche dei dati sono indipendenti e presenti in valori booleani. Il multinomiale Naive Bayes si basa anche su un modello basato sugli eventi. Ha le caratteristiche dei dati in forma vettoriale, che rappresenta le frequenze rilevanti in base al verificarsi degli eventi.
