Introduzione alla funzione di densità di probabilità [formula, proprietà, applicazioni, esempi]

La funzione di densità di probabilità (PDF) è un'espressione statistica che denota la distribuzione di probabilità di una variabile casuale discreta. La distribuzione di probabilità, in termini semplici, può essere definita come una probabilità di esito di una variabile casuale come un'azione o un ETF. Le variabili discrete si verificano in contrasto con una variabile casuale continua il cui valore accurato può essere determinato.

Ad esempio, il valore di scrip in un mercato azionario ha solo due punti decimali (ad esempio, 65,76) in una variabile casuale discreta invece di una variabile continua con un numero qualsiasi di punti decimali (esempio: 65,7685434567).

Una funzione di densità di probabilità è uno strumento statistico utilizzato per determinare la probabilità del risultato di una variabile casuale discreta. Quando vengono tracciati su un grafico, i PDF sembrano identici a una curva a campana in cui l'area sotto la curva rappresenta la probabilità del risultato.

Quando proiettata come un modello grafico, l'area sotto la curva rappresenta l'intervallo in cui cadranno i valori delle variabili casuali discrete. Pertanto, l'area totale sotto la curva è uguale alla probabilità del risultato della variabile.

La funzione di densità di probabilità può determinare la probabilità che una variabile casuale rientri in uno specifico intervallo di valori.

In genere, le funzioni di densità di probabilità analizzano i rischi e le entrate potenziali associati a un fondo specifico nel mercato azionario.

Condizioni che devono essere soddisfatte da una funzione per essere considerata una funzione di densità di probabilità

Il valore di una variabile discreta può essere misurato con precisione in contrasto con una variabile continua che può avere un numero infinito di valori. Qualsiasi funzione deve soddisfare le due condizioni seguenti per essere una funzione di densità di probabilità:

• Il valore f(x) per ogni possibile valore della variabile casuale dovrebbe essere positivo (non negativo).
• Il valore integrale dell'area totale della curva (integrale di tutti i possibili valori della variabile casuale) dovrebbe essere 1.

Differenza tra funzione di densità di probabilità e funzione di distribuzione di probabilità

Le variabili casuali possono avere molti valori. La descrizione di ogni possibile valore che una variabile casuale può avere è chiamata distribuzione di probabilità.

La distribuzione di probabilità fornisce un insieme di risultati e le relative probabilità. La funzione statistica che rappresenta una distribuzione di probabilità continua è nota come funzione di densità di probabilità.

Esiste un altro strumento statistico che rappresenta una distribuzione di probabilità discreta chiamata funzione di massa di probabilità. Questo fornisce un resoconto dettagliato di tutti i possibili risultati e delle loro probabilità di verosimiglianza.

Espressione per le funzioni di densità di probabilità

Se la variabile casuale è discreta, la sua distribuzione di probabilità è chiamata funzione di massa di probabilità, e se è una variabile continua, la distribuzione di probabilità è chiamata funzione di densità di probabilità.

Un PDF viene utilizzato quando la variabile casuale in questione ha un intervallo di valori possibili. La loro distribuzione di probabilità viene utilizzata per determinare il valore esatto.

Sia la variabile casuale indicata con X. La funzione di densità di probabilità, f della variabile casuale X può essere espressa come

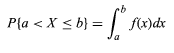
• Il valore della variabile casuale è compreso tra a e b.
• Se X indica la probabilità di selezionare un numero particolare dall'intervallo (intervallo) r e s, allora la funzione di densità di probabilità può essere espressa come

f ( x ) = 1/( s − r ) per r < x < s e f ( x ) = 0 per x < r o x > s .

• Il PDF F è rappresentato come:

F ( x ) = P { X ≤ x }

che è chiamata funzione di distribuzione o funzione di distribuzione cumulativa di X.

Considerando che la variabile casuale X ha una funzione di distribuzione di probabilità f ( x ), allora la relazione tra f e F può essere stabilita come

F ′(. x ) = f ( x )

La funzione di distribuzione di una variabile casuale discreta è diversa dalla sua funzione di distribuzione di probabilità. La relazione tra i due può essere espressa come segue:

L'aspettativa della variabile casuale è indicata come

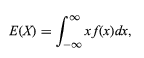
Pertanto, tutte le variabili discrete e casuali possono essere trattate in modo uniforme con l'aiuto di una teoria combinata.

La formula della funzione di densità di probabilità

La probabilità di una variabile casuale continua X su un valore fisso x è sempre 0. In questo caso, P(X = x) non può essere utilizzato. Dovrebbe essere determinato il valore della X compreso tra un intervallo di valori (a, b). Per determinare lo stesso, viene utilizzata la seguente formula.

Proprietà di una funzione di densità di probabilità

Una variabile casuale continua che assume il suo valore tra l'intervallo (a,b), ad esempio, sarà stimata calcolando l'area sotto la curva e l'asse X tracciato con (a) come limite inferiore e (b) come suo limite superiore. La funzione di densità di probabilità per quanto sopra è rappresentata come:

La funzione di densità di probabilità è positiva (non negativa) per tutti i valori possibili. Ciò significa f(x)≥ 0, per ogni x. L'area compresa tra la curva di densità e l'asse X (asse orizzontale) è uguale a 1.

Questo può anche essere indicato come:

La curva della funzione di densità è continua per tutto l'intervallo dato, che è chiaramente definito rispetto a una serie di valori continui o al dominio della variabile.

Partecipa al corso di Machine Learning online dalle migliori università del mondo: master, programmi post-laurea per dirigenti e programma di certificazione avanzato in ML e AI per accelerare la tua carriera.

Applicazioni della funzione di densità di probabilità

• La funzione di densità di probabilità viene utilizzata nella modellazione annuale dei livelli di concentrazione di NO nell'atmosfera.
• Modellazione della combustione di motori diesel.
• In statistica, la funzione di densità di probabilità viene utilizzata per determinare le possibilità del risultato di una variabile casuale.

Esempi di funzione di densità di probabilità

• Esempio 1

Di seguito è riportato un esempio di come viene utilizzata la funzione di densità di probabilità (PDF) per determinare il potenziale di rischio di un investitore nel mercato azionario:

Innanzitutto, i PDF vengono generati come strumento grafico basato su informazioni storiche.

La forma più comune di PDF è la proiezione neutra, in cui il rischio è uguale alla ricompensa in una gamma di possibilità. Gli investitori con una minore capacità di assunzione di rischi saranno premiati solo con profitti limitati e quindi si troveranno sotto il lato sinistro della curva a campana. Al contrario, è probabile che gli investitori con un'elevata capacità di assunzione di rischio vengano premiati con rendimenti più elevati e, pertanto, cadano sotto il lato destro della curva.

La maggior parte degli investitori rientra nella capacità media di assunzione di rischio e quindi occupa la metà della curva.

Questo aiuta ad analizzare la categoria di investitori in base ai dati ricevuti. Questo aiuta i broker del mercato azionario a identificare la loro categoria target di clienti per vendere i loro prodotti.

• Esempio 2

Una delle applicazioni essenziali della funzione di densità di probabilità è la variabile casuale gaussiana, nota anche come variabile casuale normale.

In entrambi i casi, il grafico fornisce una curva a campana per la funzione di densità di probabilità.

La densità può essere espressa come

Il grafico dell'equazione di densità sopra è riportato di seguito.

L'area sotto la curva rappresenta il valore effettivo della variabile casuale gaussiana.

Conclusione

La funzione di densità di probabilità gioca un ruolo fondamentale nell'apprendimento automatico. Per gli studenti che cercano una carriera nell'apprendimento automatico e nell'intelligenza artificiale, consigliamo vivamente di iscriversi al programma di certificazione avanzato IIT di upGrad in Machine Learning . Il programma è personalizzato e progettato per fornire ai professionisti senior la possibilità di implementare modelli di machine learning utilizzando la tecnologia di cloud computing.

Il curriculum è progettato dalla facoltà di IIT Madras e da esperti del settore per rendere il processo di apprendimento più pertinente e pratico. Il programma offre una certificazione riconosciuta a livello mondiale dall'ambito college di ingegneria n. 1 in India e supporto per il posizionamento a 360 gradi da upGrad.

Inoltre, hai numerose opportunità di collaborare a progetti su larga scala con la base di studenti pagati di upGrad di oltre 40.000.

Vai al nostro sito Web per iniziare il tuo viaggio di apprendimento!