Introduzione alla regressione multivariata nell'apprendimento automatico: guida completa

Non è un segreto che la tecnologia odierna sia basata sui dati. I dati possono essere solo una raccolta di cifre, ma possono essere elaborati in modo significativo per estrarre produttività e intraprendenza affinché le aziende rimangano competitive e sostenibili a lungo termine. L'analisi dei dati è la risposta per ricavare stime accurate da informazioni grezze.

L'analisi dei dati è una tecnica che coinvolge idee statistiche e logiche per esaminare, elaborare e trasformare i dati in una forma utilizzabile. Le soluzioni disegnate dall'analisi dei dati vengono utilizzate nelle aziende per prendere decisioni vitali. La scienza dei dati insieme all'analisi dei dati viene utilizzata per prevedere i risultati futuri con elevata precisione. È un processo di impiego di tecniche scientifiche e algoritmi per ottenere informazioni valide da un pool di dati.

Un problema comune affrontato dai professionisti dei dati è il modo in cui determinare se esiste una relazione statistica tra una variabile di risposta (indicata da Y) e variabili esplicative (indicate da Xi).

La risposta a questa preoccupazione è l'analisi di regressione. Comprendiamo questo in modo più dettagliato.

Che cos'è l'analisi di regressione?

L'analisi di regressione è uno dei metodi più diffusi nell'analisi dei dati che segue un algoritmo di apprendimento automatico controllato o supervisionato. È una tecnica efficace per identificare e stabilire una relazione tra variabili nei dati.

L'analisi di regressione implica l'ordinamento delle variabili praticabili utilizzando strategie matematiche per trarre conclusioni altamente accurate su tali variabili ordinate.

Che cos'è la regressione multivariata?

Multivariate è un algoritmo di Machine Learning controllato o supervisionato che analizza più variabili di dati. È una continuazione della regressione multipla che coinvolge una variabile dipendente e molte variabili indipendenti. L'output è previsto in base al numero di variabili indipendenti.

La regressione multivariata determina una formula che spiega la risposta simultanea dei fattori presenti nelle variabili ai cambiamenti nelle altre. Sono usati per studiare i dati in vari campi. Ad esempio, nel settore immobiliare la regressione multivariata viene utilizzata per prevedere il prezzo di una casa in base a diversi fattori come la sua posizione, il numero di stanze e i servizi disponibili.

Funzione di costo nella regressione multivariata

La funzione di costo assegna un costo ai campioni quando il risultato di un modello si discosta dai dati osservati. L'equazione della funzione di costo è il totale del quadrato della differenza tra il valore previsto e il valore effettivo diviso per due volte la lunghezza del set di dati.

Ecco un esempio :

Risultato :

Fonte

Come utilizzare l'analisi di regressione multivariata?

I processi coinvolti nell'analisi di regressione multivariata includono la selezione delle caratteristiche, l'ingegnerizzazione delle caratteristiche, la normalizzazione delle caratteristiche, le funzioni di perdita di selezione, l'analisi delle ipotesi e la creazione di un modello di regressione.

1. Selezione delle caratteristiche: è il passaggio più importante nella regressione multivariata. Conosciuto anche come selezione delle variabili, questo processo implica la selezione di variabili praticabili per costruire modelli efficienti.
2. Normalizzazione delle funzionalità: implica il ridimensionamento delle funzionalità per mantenere una distribuzione semplificata e rapporti di dati. Questo aiuta in una migliore analisi dei dati. Il valore di tutte le caratteristiche può essere modificato in base alle esigenze.
3. Selezione della funzione di perdita e dell'ipotesi : la funzione di perdita viene utilizzata per prevedere gli errori. La funzione di perdita entra in gioco quando la previsione dell'ipotesi cambia rispetto alle cifre effettive. Qui, l'ipotesi rappresenta il valore previsto dalla caratteristica o variabile.
4. Parametro di ipotesi di correzione : il parametro dell'ipotesi è fisso o impostato in modo tale da ridurre al minimo la funzione di perdita e migliorare la previsione.
5. Ridurre la funzione di perdita : La funzione di perdita viene minimizzata generando un algoritmo specifico per la minimizzazione della perdita sul set di dati che a sua volta facilita l'alterazione dei parametri dell'ipotesi. La discesa del gradiente è l'algoritmo più comunemente utilizzato per la minimizzazione delle perdite. L'algoritmo può essere utilizzato anche per altre azioni una volta completata la minimizzazione delle perdite.
6. Analizzare la funzione dell'ipotesi : La funzione dell'ipotesi deve essere analizzata in quanto è fondamentale per prevedere i valori. Dopo che la funzione è stata analizzata, viene quindi testata sui dati di test.

Esaminiamo ora i due modi in cui è possibile utilizzare la regressione multivariata.

1. Regressione lineare multivariata

La regressione lineare multivariata assomiglia alla regressione lineare semplice tranne per il fatto che nella regressione lineare multivariata, più variabili indipendenti contribuiscono alle variabili dipendenti e quindi nel calcolo vengono utilizzati più coefficienti.

• Viene utilizzato per derivare una relazione matematica tra più variabili casuali. Spiega quante più variabili indipendenti sono associate a una variabile dipendente.
• I dettagli delle variabili multiple indipendenti vengono utilizzati per fare una previsione accurata dell'influenza che hanno sulla variabile di risultato.
• Il modello di regressione lineare multivariata genera una relazione in una forma lineare (una forma di linea retta) con la migliore approssimazione di ciascun punto dati.
• L'equazione del modello di regressione lineare multivariata è:

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

dove per i=n osservazioni:

Fonte

Quando può essere utilizzata la regressione lineare?

Il modello di regressione lineare può essere utilizzato solo quando sono presenti due variabili continue di cui una dipendente e l'altra indipendente.

La variabile indipendente viene utilizzata come parametro per determinare il valore o il risultato della variabile dipendente.

2. Regressione logistica multivariata

La regressione logistica è un algoritmo utilizzato per prevedere un risultato binario basato su più variabili indipendenti. Un risultato binario ha due possibilità, o lo scenario accade (rappresentato da 1) o non accade (indicato da 0).

La regressione logistica viene utilizzata quando si lavora su dati binari, i dati in cui il risultato (o la variabile dipendente) è dicotomico.

Dove può essere utilizzata la regressione logistica?

La regressione logistica viene utilizzata principalmente per affrontare i problemi di classificazione. Ad esempio, per accertare se un'e-mail è spam o meno e se una particolare transazione è dannosa o meno. Nell'analisi dei dati, viene utilizzato per prendere decisioni calcolate per ridurre al minimo le perdite e aumentare i profitti.

La regressione logistica multivariata viene utilizzata quando esiste una variabile dipendente e più risultati. Si differenzia dalla regressione logistica per avere più di due possibili esiti.

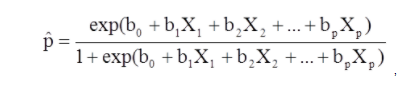
Da X1 a Xp sono variabili indipendenti distinte.

b0 to bp sono i coefficienti di regressione

Il modello di regressione logistica multipla può anche essere scritto in una forma diversa. Nel modulo sottostante, il risultato è il registro atteso delle probabilità che il risultato sia presente,

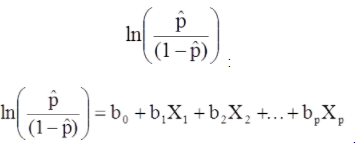
Il modello di regressione logistica multipla può anche essere scritto in una forma diversa. Nel modulo sottostante, il risultato è il registro atteso delle probabilità che il risultato sia presente.

Il lato destro dell'equazione precedente assomiglia all'equazione di regressione lineare ma il metodo per scoprire i coefficienti di regressione è diverso.

Assunzioni nel modello di regressione multivariata

• Le variabili dipendenti e indipendenti hanno una relazione lineare.
• Le variabili indipendenti non hanno una forte correlazione tra loro.
• Le osservazioni di yi sono scelte casualmente e individualmente dalla popolazione.

Assunzioni nel modello di regressione logistica multivariata

• La variabile dipendente è nominale o ordinale. Le variabili nominali hanno due o più categorie senza alcuna organizzazione significativa. Le variabili ordinali possono anche avere due o più categorie, ma hanno una struttura e possono essere classificate.
• Possono esserci variabili indipendenti singole o multiple che possono essere ordinali, continue o nominali. Le variabili continue sono quelle che possono avere valori infiniti all'interno di un intervallo specifico.
• Le variabili dipendenti sono mutuamente esclusive ed esaustive.
• Le variabili indipendenti non hanno una forte correlazione tra loro.

Vantaggi della regressione multivariata

1. La regressione multivariata ci aiuta a studiare le relazioni tra più variabili nel set di dati.
2. La correlazione tra variabili dipendenti e indipendenti aiuta a prevedere il risultato.
3. È uno degli algoritmi più convenienti e popolari utilizzati nell'apprendimento automatico.

Svantaggi della regressione multivariata

• La complessità delle tecniche multivariate richiede calcoli matematici complessi.
• Non è facile interpretare l'output del modello di regressione multivariata poiché ci sono incoerenze negli output di perdita ed errore.
• I modelli di regressione multivariata non possono essere applicati a set di dati più piccoli; sono progettati per produrre output accurati quando si tratta di set di dati più grandi.

Se desideri saperne di più sulla regressione multivariata e altri argomenti complessi di scienza dei dati, upGrad ha la soluzione giusta per te. Il nostro corso di Master of Science in Data Science di 18 mesi presso la Liverpool John Moores University copre oltre 500 ore di apprendimento rigorose, 25 sessioni di coaching (tenuto su base 1:8) e oltre 20 sessioni dal vivo. upGrad offre anche assistenza didattica 1:1 e supporto di orientamento professionale a 360° per consentire agli studenti di trasformare le loro carriere. Gli studenti possono sfruttare l'apprendimento peer-to-peer sulla piattaforma globale con oltre 40.000 studenti pagati e lavorare su progetti collaborativi in ​​sei specializzazioni funzionali per massimizzare la loro esperienza di apprendimento.