Gaussian Naive Bayes: cosa devi sapere?
Pubblicato: 2021-02-22Sommario
Bayes ingenuo gaussiano
Naive Bayes è un algoritmo probabilistico di apprendimento automatico utilizzato per molte funzioni di classificazione e si basa sul teorema di Bayes. Gaussian Naive Bayes è l'estensione dell'ingenua Bayes. Mentre altre funzioni vengono utilizzate per stimare la distribuzione dei dati, la distribuzione gaussiana o normale è la più semplice da implementare poiché sarà necessario calcolare la media e la deviazione standard per i dati di addestramento.
Cos'è l'algoritmo Naive Bayes?
Naive Bayes è un algoritmo probabilistico di apprendimento automatico che può essere utilizzato in diverse attività di classificazione. Le applicazioni tipiche di Naive Bayes sono la classificazione dei documenti, il filtraggio dello spam, la previsione e così via. Questo algoritmo si basa sulle scoperte di Thomas Bayes e da qui il suo nome.
Il nome "Naive" viene utilizzato perché l'algoritmo incorpora nel suo modello funzionalità indipendenti l'una dall'altra. Eventuali modifiche al valore di una caratteristica non influiscono direttamente sul valore di qualsiasi altra caratteristica dell'algoritmo. Il vantaggio principale dell'algoritmo Naive Bayes è che è un algoritmo semplice ma potente.
Si basa sul modello probabilistico in cui l'algoritmo può essere codificato facilmente e le previsioni vengono eseguite rapidamente in tempo reale. Quindi questo algoritmo è la scelta tipica per risolvere i problemi del mondo reale in quanto può essere ottimizzato per rispondere istantaneamente alle richieste degli utenti. Ma prima di approfondire Naive Bayes e Gaussian Naive Bayes, dobbiamo sapere cosa si intende per probabilità condizionata.
Spiegazione della probabilità condizionale
Possiamo capire meglio la probabilità condizionale con un esempio. Quando lanci una moneta, la probabilità di andare avanti o una croce è del 50%. Allo stesso modo, la probabilità di ottenere un 4 quando lanci i dadi con le facce è 1/6 o 0,16.
Se prendiamo un mazzo di carte, qual è la probabilità di ottenere una donna data la condizione che sia una picche? Poiché è già impostata la condizione che deve essere di picche, il denominatore o il set di selezione diventa 13. C'è solo una regina di picche, quindi la probabilità di prendere una regina di picche diventa 1/13 = 0,07.

La probabilità condizionata dell'evento A dato l'evento B indica la probabilità che l'evento A si verifichi dato che l'evento B è già avvenuto. Matematicamente, la probabilità condizionata di A data B può essere indicata come P[A|B] = P[A AND B] / P[B].
Consideriamo un piccolo esempio complesso. Prendi una scuola con un totale di 100 studenti. Questa popolazione può essere suddivisa in 4 categorie: studenti, insegnanti, maschi e femmine. Considera la tabella riportata di seguito:
| Femmina | Maschio | Totale | |
| Insegnante | 8 | 12 | 20 |
| Alunno | 32 | 48 | 80 |
| Totale | 40 | 50 | 100 |
Ecco qual è la probabilità condizionata che un certo residente della scuola sia un Insegnante data la condizione che sia un Uomo.
Per calcolare questo, dovrai filtrare la sottopopolazione di 60 uomini e approfondire i 12 insegnanti maschi.
Quindi, la probabilità condizionata prevista P[Insegnante | Maschio] = 12/60 = 0,2
P (Insegnante | Maschile) = P (Insegnante ∩ Maschile) / P(Maschio) = 12/60 = 0,2
Questo può essere rappresentato come un Insegnante(A) e un Maschio(B) divisi per Maschio(B). Allo stesso modo, può essere calcolata anche la probabilità condizionata di B data A. La regola che utilizziamo per Naive Bayes può essere dedotta dalle seguenti notazioni:
P (LA | B) = P (LA ∩ B) / P(B)
P (LA | LA) = P (LA ∩ B) / P(LA)
La regola di Bayes
Nella regola di Bayes, andiamo da P (X | Y) che può essere trovato dal set di dati di addestramento per trovare P (Y | X). Per ottenere ciò, tutto ciò che devi fare è sostituire A e B con X e Y nelle formule precedenti. Per le osservazioni, X sarebbe la variabile nota e Y sarebbe la variabile sconosciuta. Per ogni riga del set di dati, devi calcolare la probabilità di Y dato che X si è già verificato.
Ma cosa succede se ci sono più di 2 categorie in Y? Dobbiamo calcolare la probabilità di ogni classe Y per scoprire quella vincente.
Attraverso la regola di Bayes, andiamo da P (X | Y) per trovare P (Y | X)
Conosciuto dai dati di allenamento: P (X | Y) = P (X ∩ Y) / P(Y)
P (Evidenza | Risultato)
Sconosciuto – da prevedere per i dati del test: P (Y | X) = P (X ∩ Y) / P(X)
P (Risultato | Evidenza)

Regola di Bayes = P (Y | X) = P (X | Y) * P (Y) / P (X)
L'ingenuo Bayes
La regola di Bayes fornisce la formula per la probabilità di Y data la condizione X. Ma nel mondo reale possono esserci più variabili X. Quando si hanno funzionalità indipendenti, la regola di Bayes può essere estesa alla regola Naive Bayes. Le X sono indipendenti l'una dall'altra. La formula di Naive Bayes è più potente della formula di Bayes
Bayes ingenuo gaussiano
Finora, abbiamo visto che le X sono in categorie, ma come calcolare le probabilità quando X è una variabile continua? Se assumiamo che X segua una particolare distribuzione, puoi usare la funzione di densità di probabilità di quella distribuzione per calcolare la probabilità delle verosimiglianze.
Se assumiamo che X segua una distribuzione gaussiana o normale, dobbiamo sostituire la densità di probabilità della distribuzione normale e chiamarla Gaussiana Naive Bayes. Per calcolare questa formula, hai bisogno della media e della varianza di X.
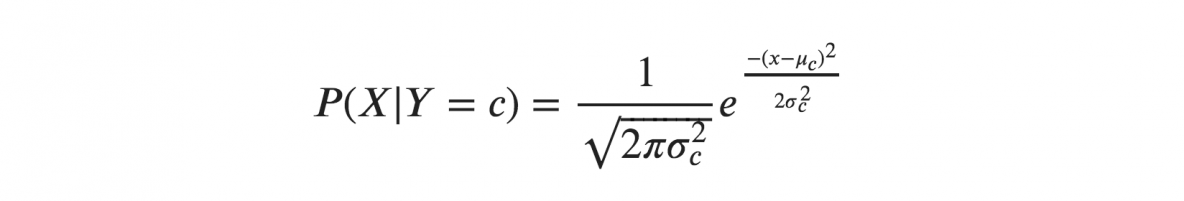
Nelle formule precedenti, sigma e mu sono la varianza e la media della variabile continua X calcolata per una data classe c di Y.
Rappresentazione per Gaussian Naive Bayes
La formula precedente ha calcolato le probabilità per i valori di input per ciascuna classe attraverso una frequenza. Possiamo calcolare la media e la deviazione standard di x per ogni classe per l'intera distribuzione.
Ciò significa che insieme alle probabilità per ciascuna classe, dobbiamo memorizzare anche la media e la deviazione standard per ogni variabile di input per la classe.
media(x) = 1/n * somma(x)
dove n rappresenta il numero di istanze e x è il valore della variabile di input nei dati.
deviazione standard(x) = sqrt(1/n * sum(xi-mean(x)^2 ))
Qui viene calcolata la radice quadrata della media delle differenze di ogni x e la media di x dove n è il numero di istanze, sum() è la funzione somma, sqrt() è la funzione radice quadrata e xi è un valore x specifico .

Previsioni con il modello Gaussiano Naive Bayes
La funzione di densità di probabilità gaussiana può essere utilizzata per fare previsioni sostituendo i parametri con il nuovo valore di input della variabile e, di conseguenza, la funzione gaussiana fornirà una stima della probabilità del nuovo valore di input.
Classificatore ingenuo di Bayes
Il classificatore Naive Bayes presuppone che il valore di una caratteristica sia indipendente dal valore di qualsiasi altra caratteristica. I classificatori Naive Bayes necessitano di dati di addestramento per stimare i parametri richiesti per la classificazione. Grazie al design e all'applicazione semplici, i classificatori Naive Bayes possono essere adatti a molti scenari di vita reale.
Conclusione
Il classificatore Gaussian Naive Bayes è una tecnica di classificazione rapida e semplice che funziona molto bene senza troppi sforzi e con un buon livello di precisione.
Se sei interessato a saperne di più sull'IA e sull'apprendimento automatico, dai un'occhiata al Diploma PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi di studio e incarichi, Status di Alumni IIIT-B, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.
Impara il corso ML dalle migliori università del mondo. Guadagna master, Executive PGP o programmi di certificazione avanzati per accelerare la tua carriera.
Che cos'è un algoritmo di bayes ingenuo?
Naive bayes è un classico algoritmo di apprendimento automatico. Avendo la sua origine nella statistica, ingenuo bayes è un algoritmo semplice e potente. Naive bayes è una famiglia di classificatori basati sull'applicazione di un'analisi di probabilità condizionale. In questa analisi, la probabilità condizionata di un evento viene calcolata utilizzando la probabilità di ciascuno dei singoli eventi che costituiscono l'evento. I classificatori ingenuo bayes si trovano spesso estremamente efficaci nella pratica, specialmente quando il numero di dimensioni del set di funzionalità è elevato.
Quali sono le applicazioni dell'algoritmo di bayes ingenuo?
Naive Bayes è utilizzato nella classificazione del testo, nella classificazione dei documenti e nell'indicizzazione dei documenti. In naive bayes, ogni possibile caratteristica non ha alcun peso assegnato nella fase di pre-elaborazione e i pesi vengono assegnati successivamente durante l'allenamento e le fasi di riconoscimento. Il presupposto di base dell'algoritmo di bayes ingenuo è che le caratteristiche siano indipendenti.
Che cos'è l'algoritmo gaussiano Naive Bayes?
Gaussian Naive Bayes è un algoritmo di classificazione probabilistica basato sull'applicazione del teorema di Bayes con forti ipotesi di indipendenza. Nel contesto della classificazione, l'indipendenza si riferisce all'idea che la presenza di un valore di una caratteristica non influenza la presenza di un altro (a differenza dell'indipendenza nella teoria della probabilità). Ingenuo si riferisce all'uso di un presupposto che le caratteristiche di un oggetto siano indipendenti l'una dall'altra. Nel contesto dell'apprendimento automatico, i classificatori ingenui di Bayes sono noti per essere altamente espressivi, scalabili e ragionevolmente accurati, ma le loro prestazioni si deteriorano rapidamente con la crescita del set di formazione. Una serie di caratteristiche contribuisce al successo dei classificatori ingenui di Bayes. In particolare, non richiedono alcuna messa a punto dei parametri del modello di classificazione, si adattano bene alle dimensioni del set di dati di addestramento e possono gestire facilmente funzionalità continue.
