Diversi tipi di modelli di regressione che devi conoscere

I problemi di regressione sono comuni nell'apprendimento automatico e la tecnica più comune per risolverli è l'analisi di regressione. Si basa sulla modellazione dei dati e implica l'elaborazione della linea di adattamento migliore, che passa attraverso tutti i punti dati in modo che la distanza tra la linea e ciascun punto dati sia minima. Sebbene esistano molte diverse tecniche di analisi di regressione, la regressione lineare e logistica sono le più importanti. Il tipo di modello di analisi di regressione che utilizziamo dipenderà alla fine dalla natura dei dati coinvolti.

Scopriamo di più sull'analisi di regressione e sui diversi tipi di modelli di analisi di regressione.

Che cos'è l'analisi di regressione?

L'analisi di regressione è una tecnica di modellazione predittiva per determinare la relazione tra le variabili dipendenti (obiettivo) e le variabili indipendenti in un set di dati. Viene in genere utilizzato quando la variabile target contiene valori continui e le variabili dipendenti e indipendenti condividono una relazione lineare o non lineare. Pertanto, le tecniche di analisi di regressione trovano impiego nel determinare la relazione dell'effetto causale tra variabili, modelli di serie temporali e previsioni. Ad esempio, la relazione tra le vendite e le spese pubblicitarie di un'azienda può essere studiata al meglio utilizzando l'analisi di regressione.

Tipi di analisi di regressione

Esistono molti diversi tipi di tecniche di analisi di regressione che possiamo utilizzare per fare previsioni. Inoltre, l'uso di ciascuna tecnica è guidato da fattori quali il numero di variabili indipendenti, la forma della retta di regressione e il tipo di variabile dipendente.

Cerchiamo di capire alcuni dei metodi di analisi di regressione più comunemente usati:

1. Regressione lineare

La regressione lineare è la tecnica di modellazione più conosciuta e presuppone una relazione lineare tra una variabile dipendente (Y) e una variabile indipendente (X). Stabilisce questa relazione lineare utilizzando una retta di regressione, nota anche come retta di adattamento. La relazione lineare è rappresentata dall'equazione Y = c+m*X + e, dove 'c' è l'intercetta, 'm' è la pendenza della linea e 'e' è il termine di errore.

Il modello di regressione lineare può essere semplice (con una variabile dipendente e una indipendente) o multiplo (con una variabile dipendente e più di una variabile indipendente).

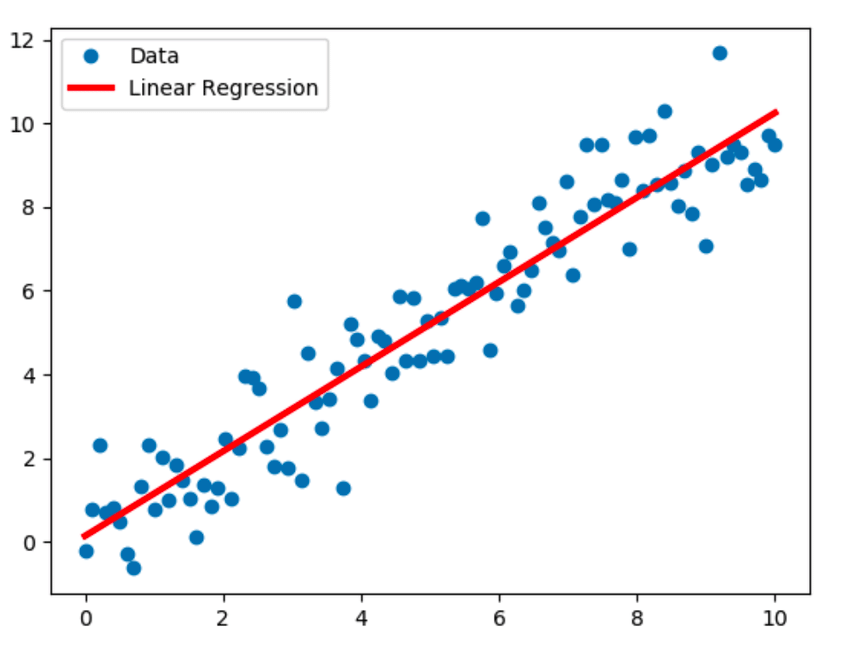
Fonte

2. Regressione logistica

La tecnica di analisi della regressione logistica trova impiego quando la variabile dipendente è discreta. In altre parole, questa tecnica viene utilizzata per stimare la probabilità di eventi che si escludono a vicenda come pass/fail, vero/falso, 0/1, ecc. Quindi, la variabile target può avere solo uno di due valori e una curva sigmoidea rappresenta la sua relazione con la variabile indipendente. Il valore della probabilità è compreso tra 0 e 1.

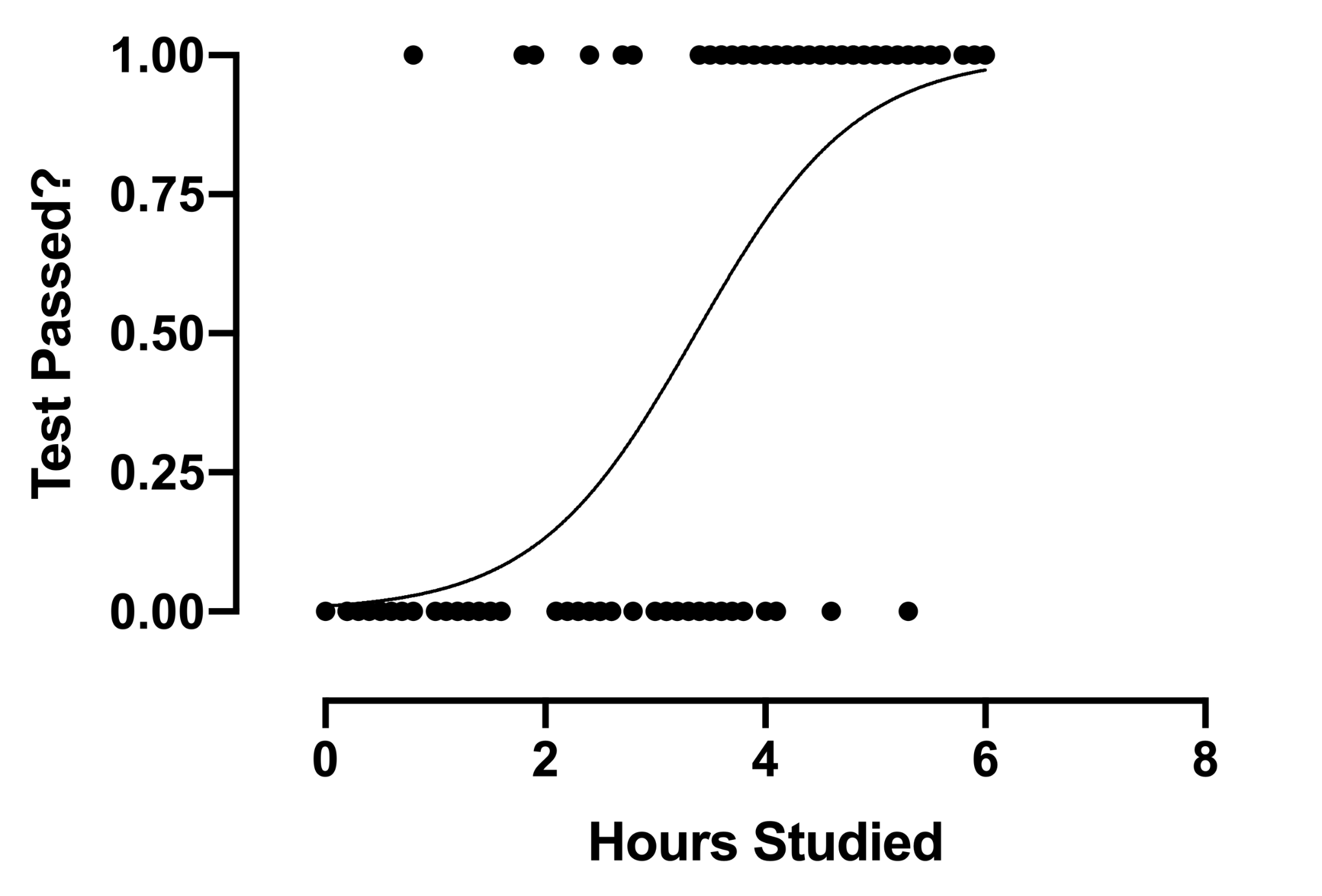
Fonte

3. Regressione polinomiale

La tecnica di analisi della regressione polinomiale modella una relazione non lineare tra le variabili dipendenti e indipendenti. È una forma modificata del modello di regressione lineare multipla, ma la linea di adattamento migliore che passa attraverso tutti i punti dati è curva e non diritta.

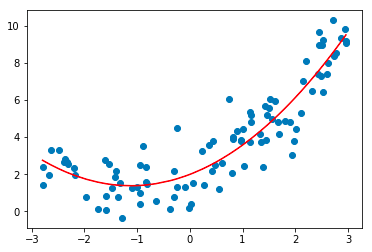
Fonte

4. Regressione della cresta

La tecnica di analisi della regressione della cresta viene utilizzata quando i dati mostrano multicollinearità; cioè, le variabili indipendenti sono altamente correlate. Sebbene le stime dei minimi quadrati nella multicollinearità siano imparziali, le loro varianze sono sufficientemente grandi da deviare il valore osservato dal valore reale. La regressione di cresta riduce al minimo gli errori standard introducendo un grado di distorsione nelle stime di regressione.

La lambda (λ) nell'equazione di regressione della cresta risolve il problema della multicollinearità.

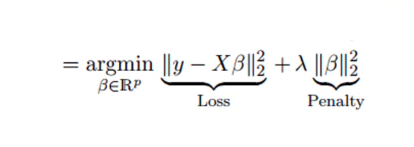
Fonte

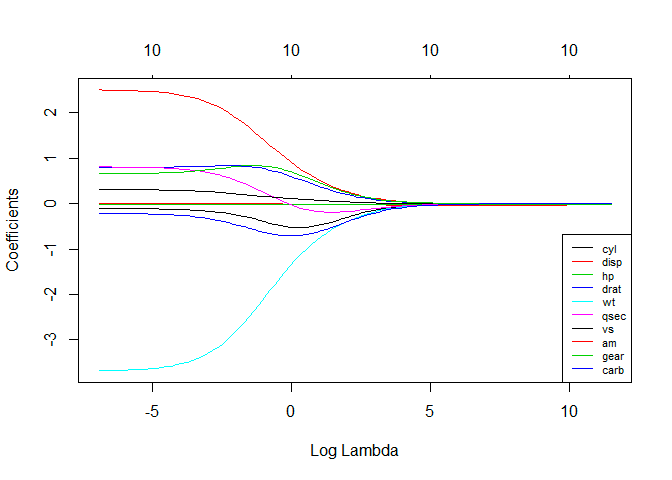
Fonte

5. Regressione con lazo

Come la regressione della cresta, la tecnica di regressione con lazo (Least Absolute Shrinkage and Selection Operator) penalizza la dimensione assoluta del coefficiente di regressione. Inoltre, la tecnica di regressione con lazo utilizza la selezione variabile, che si traduce in una riduzione dei valori dei coefficienti verso lo zero assoluto.

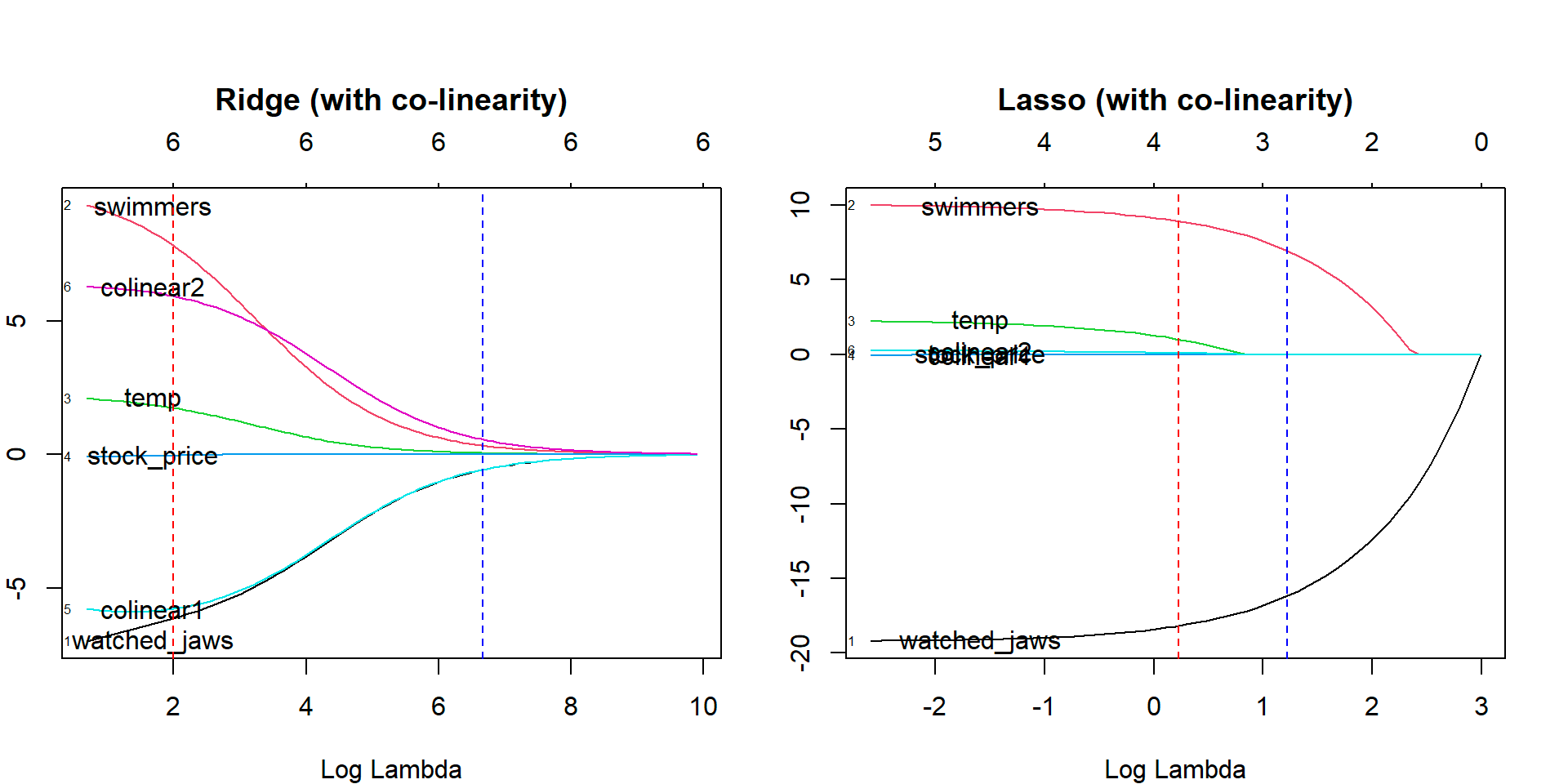
Fonte

6. Regressione quantilica

La tecnica dell'analisi di regressione quantile è un'estensione dell'analisi di regressione lineare. Viene utilizzato quando le condizioni per la regressione lineare non sono soddisfatte o i dati presentano valori anomali. La regressione quantile trova applicazioni in statistica ed econometria.

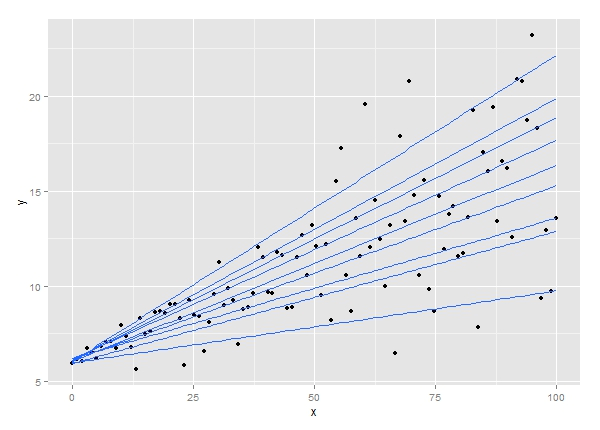
Fonte

7. Regressione lineare bayesiana

La regressione lineare bayesiana è uno dei tipi di tecniche di analisi di regressione nell'apprendimento automatico che utilizza il teorema di Bayes per determinare il valore dei coefficienti di regressione. Invece di scoprire i minimi quadrati, questa tecnica determina la distribuzione a posteriori delle caratteristiche. Di conseguenza, la tecnica ha una maggiore stabilità rispetto alla semplice regressione lineare.

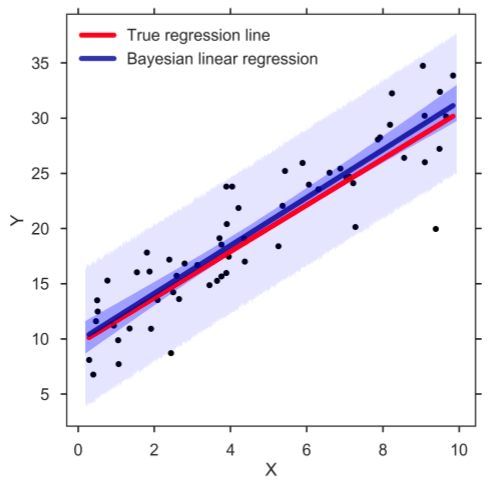
Fonte

8. Regressione delle componenti principali

La tecnica di regressione delle componenti principali viene in genere utilizzata per analizzare i dati di regressione multipla con multicollinearità. Come la tecnica di regressione della cresta, il metodo di regressione delle componenti principali riduce al minimo gli errori standard impartendo un grado di distorsione alle stime di regressione. La tecnica prevede due passaggi: in primo luogo, l'analisi delle componenti principali viene applicata ai dati di addestramento, quindi i campioni trasformati vengono utilizzati per addestrare un regressore.

9. Regressione parziale dei minimi quadrati

La tecnica di regressione dei minimi quadrati parziali è uno dei tipi rapidi ed efficienti di tecniche di analisi di regressione basate sulla covarianza. È utile per problemi di regressione in cui il numero di variabili indipendenti è elevato con probabile multicollinearità tra le variabili. La tecnica riduce le variabili a un insieme più piccolo di predittori, che vengono quindi utilizzati per eseguire una regressione.

10. Regressione della rete elastica

La tecnica di regressione della rete elastica è un ibrido dei modelli di regressione cresta e lazo ed è utile quando si tratta di variabili altamente correlate. Utilizza le penalità dei metodi di regressione con cresta e lazo per regolarizzare i modelli di regressione.

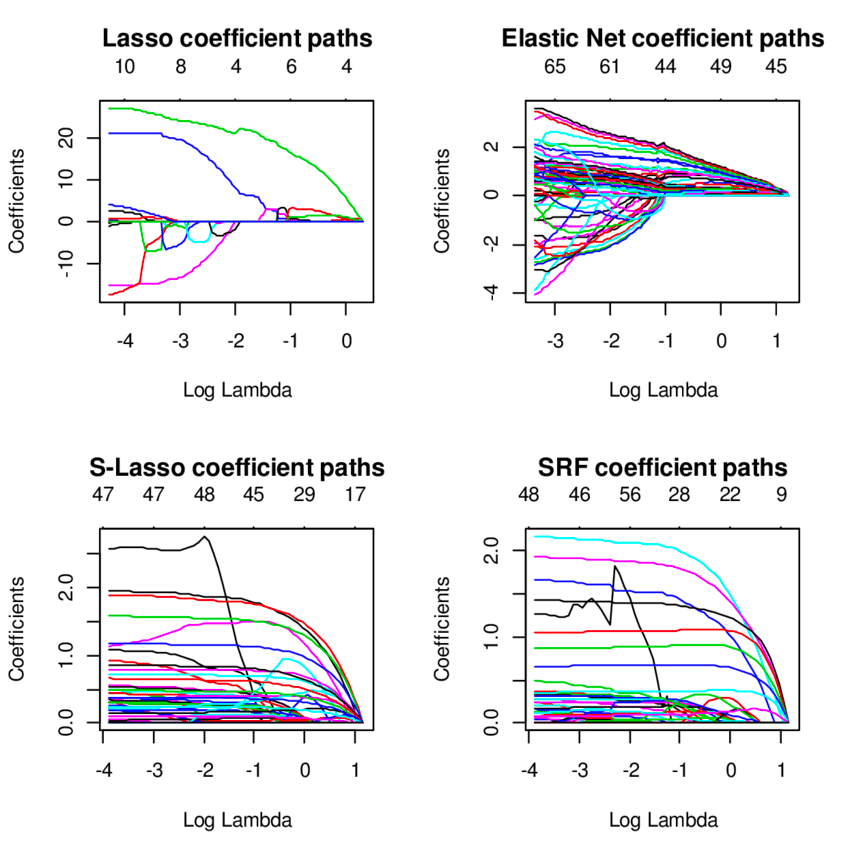
Fonte

Sommario

Oltre alle tecniche di analisi della regressione che abbiamo discusso qui, nell'apprendimento automatico vengono utilizzati molti altri tipi di modelli di regressione, come la regressione ecologica, la regressione graduale, la regressione a coltello e la regressione robusta. Il caso d'uso specifico di tutti questi diversi tipi di tecniche di regressione dipende dalla natura dei dati disponibili e dal livello di accuratezza che può essere raggiunto. Nel complesso, l'analisi di regressione presenta due vantaggi principali. Questi sono i seguenti:

• Indica la relazione tra una variabile dipendente e una variabile indipendente.

• Mostra la forza dell'impatto delle variabili indipendenti su una variabile dipendente.

Via da seguire: guadagna un Master of Science in Machine Learning e AI

Stai cercando un programma online completo per prepararti a una carriera nell'apprendimento automatico e nell'intelligenza artificiale?

upGrad offre un Master of Science in Machine Learning e AI in associazione con la Liverpool John Moores University e IIIT Bangalore per produrre professionisti dell'IA versatili e scienziati dei dati.

Il programma online completo di 20 mesi è progettato specificamente per i professionisti che desiderano padroneggiare concetti e abilità avanzati come Deep Learning, NLP, modelli grafici, Reinforcement Learning e simili. Inoltre, il programma intende fornire una solida base statistica insieme a linguaggi e strumenti di programmazione chiave come Python, Keras, TensorFlow, Kubernetes, MySQL e altri.

Punti salienti del programma:

• Master presso la Liverpool John Moores University
• PGP esecutivo da IIIT Bangalore
• Oltre 40 sessioni dal vivo, oltre 12 casi di studio e progetti, 11 incarichi di codifica, sei progetti capstone
• Oltre 25 sessioni di tutoraggio con esperti del settore
• Assistenza professionale a 360 gradi e supporto all'apprendimento
• Opportunità di networking peer-to-peer

Con una facoltà di livello mondiale, pedagogia, tecnologia ed esperti del settore, upGrad è emersa come la più grande piattaforma EdTech superiore dell'Asia meridionale e ha avuto un impatto su oltre 500.000 professionisti in tutto il mondo. Iscriviti oggi per entrare a far parte degli oltre 40.000 studenti globali di upGrad in oltre 80 paesi!