Derivato della regola della catena nell'apprendimento automatico: spiegazione

L'apprendimento automatico si è evoluto fino a diventare uno dei campi più discussi e ricercati negli ultimi anni, e per tutte le buone ragioni. Ogni giorno vengono scoperti nuovi modelli e applicazioni dell'apprendimento automatico e ricercatori di tutto il mondo stanno lavorando per il prossimo grande traguardo.

Di conseguenza, c'è stato un crescente interesse per i professionisti con background diversi per passare all'apprendimento automatico e far parte di questa rivoluzione in corso. Se sei uno di questi appassionati di apprendimento automatico che cerca di muovere i primi passi, ti diciamo che inizia con la comprensione delle basi della matematica e della statistica prima di ogni altra cosa.

Uno di questi argomenti vitali in matematica che è molto rilevante per l'apprendimento automatico sono i derivati. Dalla tua conoscenza di base del calcolo, ricorderesti che la derivata di qualsiasi funzione è il tasso di cambiamento istantaneo di quella funzione. In questo blog approfondiremo i derivati ​​ed esploreremo la regola della catena. Vedremo come cambia l'output di una particolare funzione quando cambiamo alcune variabili indipendenti nell'equazione. Con la conoscenza dei derivati ​​delle regole della catena, sarai in grado di lavorare sulla differenziazione di funzioni più complesse che sicuramente incontrerai nell'apprendimento automatico.

Ottieni la certificazione di Machine Learning online dalle migliori università del mondo: master, programmi post-laurea per dirigenti e programma di certificazione avanzato in ML e AI per accelerare la tua carriera.

Comprendere il derivato della regola della catena

La regola della catena è essenzialmente una formula matematica che aiuta a calcolare la derivata di una funzione composta. Una funzione composita è quella composta da due o più funzioni. Quindi, se f e g sono due funzioni, la regola della catena ci aiuterebbe a trovare la derivata di funzioni composite come fog o go f.

Considerando la funzione composita fog, ecco come sarebbe la derivata della regola della catena:

La regola di cui sopra può anche essere scritta come:

Dove la funzione F è la composizione di f e g , nella forma di f(g(x)).

Supponiamo ora di avere tre variabili tali che la terza variabile (z) dipenda dalla seconda variabile (y), che a sua volta dipende dalla prima variabile (x). In tal caso, la derivata della regola della catena sarebbe simile a questa:

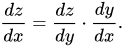In termini di deep learning, questa è anche la formula usata regolarmente per risolvere i problemi di backpropagation. Ora, poiché abbiamo detto che z dipende da y e y da x, possiamo scrivere z = f(y) e y = g(x). Questa sostituzione modificherebbe la nostra equazione differenziale nel modo seguente:

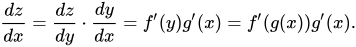Ora, diamo un'occhiata ad alcuni esempi di derivate di regole di catena per comprendere meglio la matematica dietro di esse.

Esempi e applicazioni del derivato della regola di catena

Prendiamo un esempio ben noto da Wikipedia per comprendere meglio la derivata della regola della catena. Supponi di cadere in caduta libera dal cielo. La pressione atmosferica che incontrerai durante l'autunno continuerà a cambiare continuamente. Ecco un grafico che traccia questo cambiamento della pressione atmosferica con i livelli di elevazione:

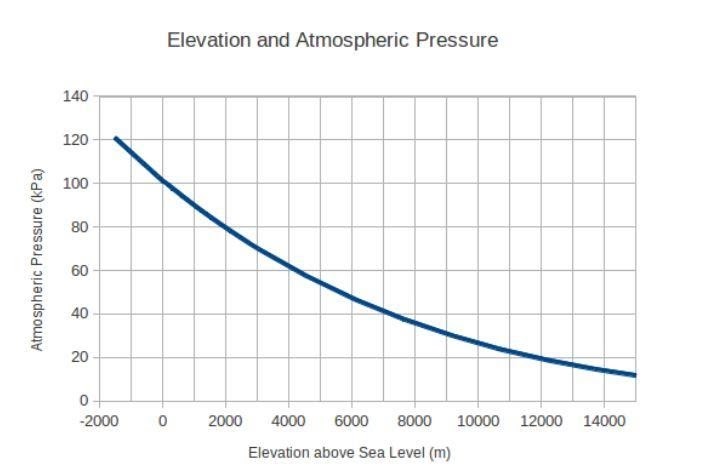
Supponiamo che la tua caduta sia iniziata a 4000 metri sul livello del mare. Inizialmente, la tua velocità era zero e il valore dell'accelerazione era di 9,8 metri al secondo quadrato a causa della gravità.

Ora, confrontiamo questa situazione con il precedente metodo della regola della catena. In questo esempio, useremo la variabile 't' per il tempo invece di x.

Allora la variabile y = g(t), che indica la distanza percorsa dall'inizio della caduta, può essere data come:

g(t) = 0,5*9,8t^2

E l'altezza dal livello del mare può essere data da una variabile 'h', che sarà pari a 400-g(t).

Assumiamo che, sulla base di un modello, possiamo anche scrivere la funzione della pressione atmosferica a qualsiasi altezza h come:

f(h) = 101325 e−0,0001h

Ora puoi distinguere tra le due equazioni in base alle loro variabili dipendenti per ottenere i seguenti risultati:

g′(t) = −9,8t,

Qui, g'(t) dice il valore della tua velocità in ogni momento t.

f′(h) = −10,1325e−0,0001h

Qui f′(h) è il tasso di variazione della pressione atmosferica rispetto all'altezza h. Ora, la domanda è: possiamo combinare queste due equazioni e ricavare la velocità di variazione della pressione atm rispetto al tempo? Vediamo usando la regola della catena:

L'equazione finale che abbiamo ci fornisce il tasso di variazione della pressione atmosferica in relazione al tempo trascorso dall'autunno. In termini di apprendimento automatico, le reti neurali necessitano costantemente di aggiornamenti di peso relativi all'errore di previsione del neurone. La regola della catena aiuta a regolare questi pesi e ad avvicinare il modello di apprendimento automatico all'output corretto.

Conclusione

Come puoi vedere, la regola della catena è vantaggiosa per molti scopi. Soprattutto quando si tratta di machine learning o deep learning, la regola della catena trova grande utilità nell'aggiornamento dei pesi dei neuroni e nel miglioramento dell'efficienza complessiva del modello.

Ora che sei a conoscenza delle basi della regola della catena, vai avanti e prova alcuni problemi da solo. Cerca alcune funzioni composite e prova a trovare le loro derivate. Più ti eserciti, più chiari saranno i tuoi concetti e più facile sarà per te addestrare i tuoi modelli di machine learning! Detto questo, se sei un appassionato di machine learning ma stai lottando per muovere i primi passi in questo campo, upGrad ti copre le spalle!

Il nostro programma Executive PG in Machine Learning e AI è offerto in collaborazione con IIIT-Bangalore e ti dà la possibilità di scegliere tra sei specializzazioni rilevanti per il settore. Il corso parte dal livello base e ti porta all'apice, fornendoti supporto 1 contro 1 da esperti del settore, un forte gruppo di studenti pari e un supporto professionale a 360 gradi.