Statistiche e modello bayesiano: spiegazione

La tecnica bayesiana è un approccio alla statistica utilizzato nell'analisi dei dati e nella stima dei parametri. Questo approccio si basa sul teorema di Bayes.

La statistica bayesiana segue un principio unico in cui aiuta a determinare la distribuzione di probabilità congiunta per i parametri osservati e non osservati utilizzando un modello statistico. La conoscenza della statistica è essenziale per affrontare i problemi analitici in questo scenario.

Sin dall'introduzione del teorema di Bayes negli anni '70 del Settecento da parte di Thomas Bayes, è rimasto uno strumento indispensabile in statistica. I modelli bayesiani sono un classico sostituto dei modelli frequentisti poiché le recenti innovazioni nelle statistiche hanno contribuito a violare le pietre miliari in un'ampia gamma di settori, tra cui la ricerca medica, la comprensione delle ricerche sul Web e l'elaborazione dei linguaggi naturali (elaborazione del linguaggio naturale).

Ad esempio, l'Alzheimer è una malattia nota per rappresentare un rischio progressivo con l'invecchiamento. Tuttavia, con l'aiuto del teorema di Bayes, i medici possono stimare la probabilità che una persona abbia l'Alzheimer in futuro. Si applica anche al cancro e ad altre malattie legate all'età a cui una persona diventa vulnerabile negli ultimi anni della sua vita.

Statistiche frequenti vs statistiche bayesiane

Statistiche frequenti e statistiche bayesiane sono state costantemente oggetto di controversia e incubi per i principianti, che hanno entrambi difficoltà a scegliere tra le due. All'inizio del XX secolo, le statistiche bayesiane hanno subito la loro parte di problemi di sfiducia e accettazione. Con il tempo, tuttavia, le persone si sono rese conto dell'applicabilità dei modelli bayesiani e delle soluzioni accurate che produce.

Diamo un'occhiata alle statistiche frequenti e alle complessità ad esse associate:

Statistiche frequenti

È una metodologia inferenziale ampiamente utilizzata nel mondo della statistica. Analizza se un evento (menzionato come ipotesi) si è verificato o meno. Stima anche la probabilità che l'evento si verifichi durante l'arco dell'esperimento. L'esperimento viene ripetuto fino al raggiungimento del risultato desiderato.

I loro campioni di distribuzione sono di dimensioni reali e l'esperimento viene ripetuto teoricamente infinite volte. Ecco un esempio che mostra come le statistiche frequenti possono essere utilizzate per studiare il lancio di una moneta.

• La possibilità di avere una testata lanciando la moneta una volta è 0,5 (1/2).
• Il numero di teste indica il numero effettivo di lead ottenuti.
• La differenza tra il numero effettivo di teste e il numero previsto di teste aumenterà all'aumentare del numero di lanci.

Quindi qui, il risultato dipende dal numero di volte che l'esperimento viene ripetuto. È uno dei principali inconvenienti delle statistiche frequenti.

Altri difetti associati alle sue tecniche di progettazione e interpretazione sono diventati evidenti nel XX secolo, quando l'applicazione di frequenti statistiche ai modelli numerici era al suo apice.

Limitazioni delle statistiche frequenti

I tre principali difetti delle statistiche frequenti sono elencati di seguito:

1. Valori p variabili

I valori di p misurati per un campione con una dimensione fissa in un esperimento con un punto finale definito cambiano con qualsiasi cambiamento nel punto finale e nella dimensione del campione. Risulta in due valori p per un singolo dato che non è corretto.

2. Intervalli di confidenza incoerenti

CI (Intervallo di confidenza) dipende esclusivamente dalla dimensione del campione. Rende irrilevante il potenziale di arresto.

3. Valori stimati di CI

Gli intervalli di confidenza non sono una distribuzione di probabilità e i loro valori per un parametro sono solo una stima e non valori effettivi.

Le tre ragioni di cui sopra hanno dato vita all'approccio bayesiano che applica le probabilità a problemi statistici.

Nascita della statistica bayesiana

Il reverendo Thomas Bayes ha proposto per la prima volta l'approccio bayesiano alla statistica nel suo saggio scritto nel 1763. Questo approccio è stato pubblicato da Richard Price come una strategia con probabilità inversa per prevedere eventi futuri basati sul passato.

L'approccio si basa sul teorema di Bayes che viene spiegato di seguito:

Teorema di Bayes

L'assioma della probabilità di Renyi esamina le probabilità condizionali, in cui le possibilità che si verifichino eventi A e B sono dipendenti o condizionali. La probabilità condizionata di base può essere scritta come:

La probabilità che si verifichi l'evento B dipende dall'evento A.

L'equazione di cui sopra è il fondamento della regola di Bayes, un'espressione matematica del teorema di Bayes che afferma:

Qui, ∩ denota l'intersezione.

La regola di Bayes può essere scritta come:

La regola di Bayes è la base della statistica bayesiana, in cui le informazioni disponibili su un particolare parametro in un modello statistico vengono confrontate e aggiornate con i dati raccolti.

La conoscenza di base è rappresentata come la distribuzione a priori, che viene poi confrontata e studiata con i dati osservati o raccolti come funzione di verosimiglianza per scoprire la distribuzione a posteriori.

Questa distribuzione a posteriori viene utilizzata per fare previsioni su eventi futuri.

Le applicazioni dell'approccio bayesiano dipendono dai seguenti parametri:

1. Definizione del modello a priori e di dati
2. Fare inferenze pertinenti
3. Scrutare e razionalizzare i modelli

Cosa sono le reti neurali bayesiane?

Le reti neurali bayesiane (BNN) sono reti create quando estendi reti standard utilizzando la metodologia statistica e modificando l'inferenza a posteriori per tenere traccia dell'overfitting. Trattandosi di un approccio bayesiano, esiste una distribuzione di probabilità associata ai parametri delle reti neurali.

Sono utilizzati per risolvere problemi complessi in cui non è disponibile un flusso libero di dati. Le reti neurali bayesiane aiutano a controllare l'overfitting in domini come la biologia molecolare e la diagnosi medica.

Si può considerare un'intera distribuzione di risposte a una domanda piuttosto che una sola possibilità utilizzando le reti neurali bayesiane. Ti aiutano a determinare la selezione/confronto del modello e ad affrontare i problemi che implicano la regolarizzazione.

La statistica bayesiana offre strumenti matematici per razionalizzare e aggiornare la conoscenza soggettiva relativa a nuovi dati o prove scientifiche. A differenza dell'approccio statistico frequente, funziona sulla base del presupposto che le probabilità dipendono dalla frequenza degli eventi che si ripetono nelle stesse condizioni.

In breve, la tecnica bayesiana è un'estensione del presupposto e dell'opinione di un individuo. L'aspetto chiave del modello bayesiano che lo rende più efficiente è la sua comprensione del fatto che gli individui differiscono nelle loro opinioni in base al tipo di informazioni che ricevono.

Tuttavia, quando emergono nuove prove e dati, gli individui hanno un punto di convergenza, l' inferenza bayesiana . Questo aggiornamento razionale è la particolarità della statistica bayesiana che la rende più efficace sui problemi analitici.

Qui, la probabilità di 0 viene applicata quando non c'è speranza che si verifichi un evento e la probabilità di 1 viene applicata quando è sicuro che l'evento si verificherà. Una probabilità compresa tra 0 e 1 dà spazio ad altri potenziali risultati.

La regola di Bayes viene ora applicata per ottenere un'inferenza bayesiana per ottenere un'inferenza migliore dal modello.

Come si applica la regola di Bayes per ottenere l'inferenza bayesiana?

Considera l'equazione:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) denota la distribuzione a priori,

P(θ|D) denota la credenza a posteriori,

P(D) rappresenta l'evidenza,

P(D|θ) indica la verosimiglianza.

L'obiettivo principale dell'inferenza bayesiana è offrire un metodo razionale e matematicamente accurato per fondere le credenze con le prove per ottenere credenze posteriori aggiornate. Le credenze posteriori possono essere utilizzate come credenze precedenti quando vengono generati nuovi dati. Pertanto, l'inferenza bayesiana aiuta ad aggiornare continuamente le credenze con l'aiuto della regola di Bayes.

Considerando lo stesso esempio di lancio di monete, il modello bayesiano aggiorna la procedura dalle credenze precedenti a quelle posteriori con nuovi lanci di monete. Il metodo bayesiano fornisce le seguenti probabilità.

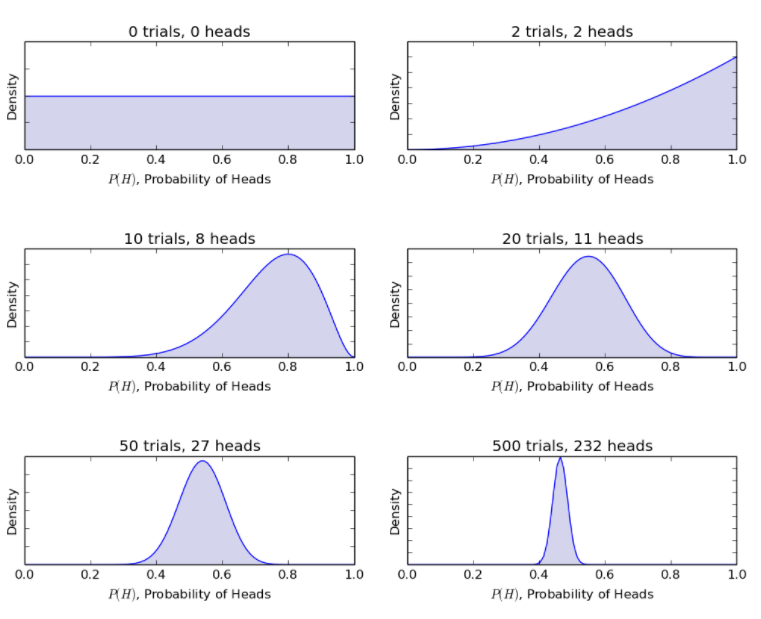
Fonte

Pertanto, il modello bayesiano consente di razionalizzare uno scenario incerto con informazioni limitate a uno scenario più definito con una notevole quantità di dati.

Notevoli differenze tra il modello bayesiano e il modello frequentista

Statistiche frequenti

Statistica bayesiana

L'obiettivo è considerato come una stima puntuale e CI

L'obiettivo è considerato come una distribuzione a posteriori

La procedura parte dalle osservazioni

Il processo inizia dalla distribuzione precedente

Ogni volta che vengono fatte nuove osservazioni, l'approccio frequentista ricalcola il modello esistente.

Ogni volta che vengono fatte nuove osservazioni, la distribuzione a posteriori (ideologia/ipotesi) viene aggiornata

Esempi: Stima della media, t-test e ANOVA.

Esempi: Stima della distribuzione a posteriori della media e sovrapposizione di intervalli ad alta densità.

Vantaggi della statistica bayesiana

• Fornisce un mezzo organico e semplice per fondere informazioni preconcette con una solida struttura con prove scientifiche. Le informazioni passate su un parametro possono essere utilizzate per formare una distribuzione precedente per indagini future. Le inferenze aderiscono al teorema di Bayes.
• Le inferenze da un modello bayesiano sono logiche e matematicamente accurate e non assunzioni grossolane. La precisione rimane costante indipendentemente dalle dimensioni del campione.
• La statistica bayesiana segue il principio di verosimiglianza. Quando due diversi campioni hanno una funzione di verosimiglianza comune per una credenza θ, tutte le inferenze sulla credenza dovrebbero essere simili. Le tecniche statistiche classiche non seguono il principio di verosimiglianza.
• Le soluzioni di un'analisi bayesiana possono essere facilmente interpretate.
• Offre una piattaforma favorevole per vari modelli come modelli gerarchici e problemi di dati incompleti. I calcoli di tutti i modelli parametrici possono essere virtualmente tracciati con l'aiuto di altre tecniche numeriche.

Applicazioni di successo dei modelli bayesiani nella storia

I metodi bayesiani hanno avuto molte applicazioni di successo durante la seconda guerra mondiale. Alcuni di loro sono elencati di seguito:

• Uno statistico russo, Andrey Kolmogorov , utilizzò con successo i metodi bayesiani per migliorare l'efficienza dell'artiglieria russa.
• I modelli bayesiani sono stati utilizzati per infrangere i codici delle barche a U tedesche.
• Un matematico americano di origine francese, Bernard Koopman, aiutò gli alleati a identificare la posizione degli U-Boot tedeschi con l'aiuto di modelli bayesiani per intercettare le trasmissioni radio.

Se desideri saperne di più sulle statistiche bayesiane, ecco la certificazione avanzata di upGrad in Machine Learning e Cloud per comprendere i concetti sottostanti attraverso progetti di settore e casi di studio reali. Il corso di 12 mesi è offerto da IIT Madras e supporta l'apprendimento autonomo.

Contattaci per ulteriori dettagli.