Esempio di rete bayesiana [con rappresentazione grafica]

introduzione

In statistica, i modelli probabilistici vengono utilizzati per definire una relazione tra variabili e possono essere utilizzati per calcolare le probabilità di ciascuna variabile. In molti problemi, ci sono un gran numero di variabili. In questi casi, i modelli completamente condizionali richiedono un'enorme quantità di dati per coprire ogni singolo caso delle funzioni di probabilità che possono essere intrattabili da calcolare in tempo reale. Ci sono stati diversi tentativi di semplificare i calcoli di probabilità condizionale come il Naive Bayes, ma ancora non si rivela efficiente in quanto riduce drasticamente diverse variabili.

L'unico modo è sviluppare un modello in grado di preservare le dipendenze condizionali tra variabili casuali e l'indipendenza condizionale in altri casi. Questo ci porta al concetto di reti bayesiane. Queste reti bayesiane ci aiutano a visualizzare efficacemente il modello probabilistico per ciascun dominio ea studiare la relazione tra variabili casuali sotto forma di un grafico di facile utilizzo.

Impara il corso ML dalle migliori università del mondo. Guadagna master, Executive PGP o programmi di certificazione avanzati per accelerare la tua carriera.

Cosa sono le reti bayesiane?

Per definizione, le reti bayesiane sono un tipo di modello grafico probabilistico che utilizza le inferenze bayesiane per i calcoli delle probabilità. Rappresenta un insieme di variabili e le sue probabilità condizionali con un grafico aciclico diretto (DAG). Sono principalmente adatti per considerare un evento che si è verificato e prevedere la probabilità che una qualsiasi delle numerose possibili cause note sia il fattore che contribuisce.

Fonte

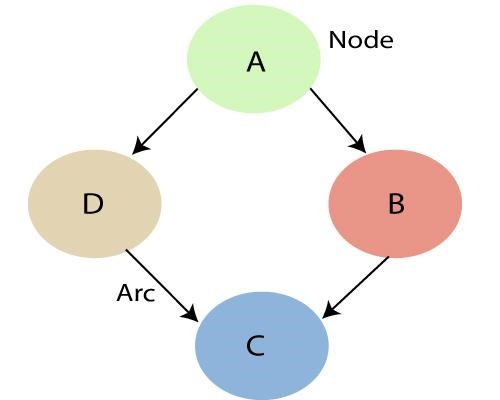
Come accennato in precedenza, utilizzando le relazioni che sono specificate dalla Rete Bayesiana, possiamo ottenere la Joint Probability Distribution (JPF) con le probabilità condizionali. Ogni nodo nel grafico rappresenta una variabile casuale e l'arco (o freccia diretta) rappresenta la relazione tra i nodi. Possono essere di natura continua o discreta.

Nel diagramma sopra A, B, C e D sono 4 variabili casuali rappresentate da nodi dati nella rete del grafico. Per il nodo B, A è il suo nodo padre e C è il suo nodo figlio. Il nodo C è indipendente dal nodo A.

Prima di entrare nell'implementazione di una rete bayesiana, ci sono alcune nozioni di base sulla probabilità che devono essere comprese.

Proprietà locale di Markov

Le reti bayesiane soddisfano la proprietà nota come Proprietà Markov locale. Afferma che un nodo è condizionatamente indipendente dai suoi non discendenti, dati i suoi genitori. Nell'esempio sopra, P(D|A, B) è uguale a P(D|A) perché D è indipendente dal suo non discendente, B. Questa proprietà ci aiuta a semplificare la distribuzione congiunta. La proprietà di Markov locale ci porta al concetto di un campo casuale di Markov che è un campo casuale attorno a una variabile che si dice segua le proprietà di Markov.

Probabilità condizionale

In matematica, la Probabilità Condizionata dell'evento A è la probabilità che l'evento A si verifichi dato che si è già verificato un altro evento B. In parole povere, p(A | B) è la probabilità che si verifichi l'evento A, dato che si verifica B. Tuttavia, esistono due tipi di possibilità di eventi tra A e B. Possono essere eventi dipendenti o eventi indipendenti. A seconda del tipo, ci sono due modi diversi per calcolare la probabilità condizionale.

• Dato che A e B sono eventi dipendenti, la probabilità condizionata è calcolata come P (A| B) = P (A e B) / P (B)
• Se A e B sono eventi indipendenti, allora l'espressione per la probabilità condizionata è data da, P(A| B) = P (A)

Distribuzione congiunta delle probabilità

Prima di entrare in un esempio di reti bayesiane, comprendiamo il concetto di distribuzione di probabilità congiunta. Considera 3 variabili a1, a2 e a3. Per definizione, le probabilità di tutte le diverse possibili combinazioni di a1, a2 e a3 sono chiamate distribuzione di probabilità congiunta.

Se P[a1,a2, a3,….., an] è il JPD delle seguenti variabili da a1 ad an, allora ci sono diversi modi per calcolare la distribuzione di probabilità congiunta come una combinazione di vari termini come,

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., an]….P[an-1|an] * P[an]

Generalizzando l'equazione di cui sopra, possiamo scrivere la distribuzione di probabilità congiunta come,

P(X i |X i-1 ,………, X n ) = P(X i | Genitori(X i ))

Esempio di reti bayesiane

Cerchiamo ora di comprendere il meccanismo delle reti bayesiane ei loro vantaggi con l'aiuto di un semplice esempio. In questo esempio, immaginiamo che ci venga affidato il compito di modellare i voti ( m ) di uno studente per un esame che ha appena dato. Dal grafico di rete bayesiano riportato di seguito, vediamo che i segni dipendono da altre due variabili. Loro sono,

• Livello esame ( e )– Questa variabile discreta denota la difficoltà dell'esame e ha due valori (0 per facile e 1 per difficile)
• Livello QI ( i ) – Rappresenta il livello del quoziente intellettivo dello studente ed è anche di natura discreta con due valori (0 per basso e 1 per alto)

Inoltre, il livello di QI dello studente ci porta anche a un'altra variabile, che è il punteggio attitudinale dello studente/ i . Ora, con i voti ottenuti dallo studente, può assicurarsi l'ammissione a una determinata università. Di seguito è riportata anche la distribuzione di probabilità per essere ammessi ( a ) in un'università.

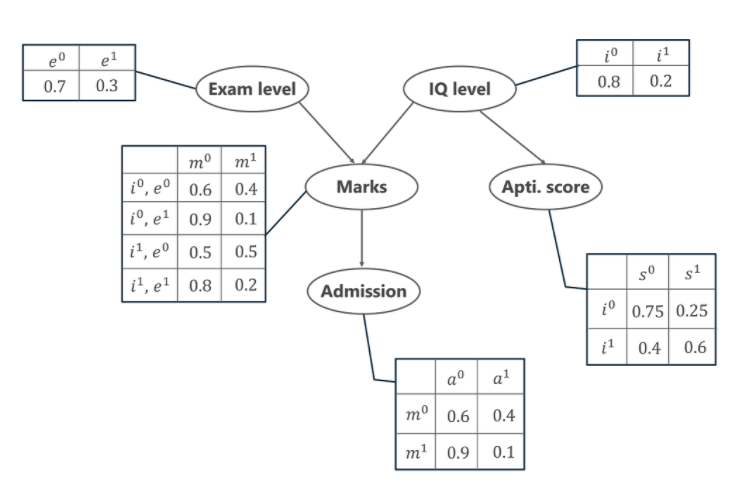
Nel grafico sopra, vediamo diverse tabelle che rappresentano i valori di distribuzione di probabilità delle 5 variabili date. Queste tabelle sono chiamate Tabella delle probabilità condizionali o CPT. Di seguito sono riportate alcune proprietà del CPT:

• La somma dei valori CPT in ogni riga deve essere uguale a 1 perché tutti i casi possibili per una determinata variabile sono esaustivi (che rappresentano tutte le possibilità).
• Se una variabile di natura booleana ha k genitori booleani, nel CPT ha 2K valori di probabilità.

Tornando al nostro problema, elenchiamo prima tutti i possibili eventi che si verificano nella tabella sopra indicata.

1. Livello esame (e)
2. Livello QI (i)
3. Punteggi attitudinali
4. Marchi (m)
5. Ammissione (a)

Queste cinque variabili sono rappresentate sotto forma di un grafico aciclico diretto (DAG) in un formato di rete bayesiana con le relative tabelle di probabilità condizionale. Ora, per calcolare la distribuzione di probabilità congiunta delle 5 variabili la formula è data da,

P[a, m, io, e, s]= P(a | m) . P(m | io, e) . P(i) . P(e) . P(s | i)

Dalla formula di cui sopra,

• P(a | m) indica la probabilità condizionata che lo studente ottenga l'ammissione in base ai voti ottenuti nell'esame.
• P(m | i, e) rappresenta i voti che lo studente segnerà in base al suo livello di QI e alla difficoltà dell'esame.
• P(i) e P(e) rappresentano la probabilità del Livello QI e del Livello dell'Esame.
• P(s | i) è la probabilità condizionata del punteggio attitudinale dello studente, dato il suo livello di QI.

Con le seguenti probabilità calcolate, possiamo trovare la Joint Probability Distribution dell'intera rete bayesiana.

Calcolo della distribuzione di probabilità congiunta

Calcoliamo ora il JPD per due casi.

Caso 1: Calcolare la probabilità che, nonostante il livello dell'esame sia difficile, lo studente con un QI basso e un punteggio attitudinale basso, riesca a superare l'esame e ad assicurarsi l'ammissione all'università.

Dalla dichiarazione del problema con la parola sopra, la distribuzione di probabilità congiunta può essere scritta come di seguito,

P[a=1, m=1, i=0, e=1, s=0]

Dalle tabelle di Probabilità Condizionale di cui sopra, i valori per le condizioni date vengono inseriti nella formula e calcolati come di seguito.

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) . P(m=1 | io=0, e=1) . P(i=0) . P(e=1) . P(s=0 | i=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0,0018

Caso 2: in un altro caso, calcola la probabilità che lo studente abbia un livello di QI e un punteggio attitudinali elevati, l'esame è facile ma non riesce a superare e non garantisce l'ammissione all'università.

La formula per il JPD è data da

P[a=0, m=0, i=1, e=0, s=1]

Così,

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) . P(m=0 | io=1, e=0) . P(i=1) . P(e=0) . P(s=1 | i=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0,0252

Quindi, in questo modo, possiamo utilizzare le reti bayesiane e le tabelle di probabilità per calcolare la probabilità di vari possibili eventi che si verificano.

Leggi anche: Idee e argomenti per progetti di apprendimento automatico

Conclusione

Esistono innumerevoli applicazioni per le reti bayesiane nel filtro antispam, nella ricerca semantica, nel recupero delle informazioni e in molti altri. Ad esempio, con un dato sintomo possiamo prevedere la probabilità che una malattia si manifesti con diversi altri fattori che contribuiscono alla malattia. Pertanto, il concetto di rete bayesiana viene introdotto in questo articolo insieme alla sua implementazione con un esempio di vita reale.

Se sei curioso di padroneggiare l'apprendimento automatico e l'intelligenza artificiale, dai una spinta alla tua carriera con un corso avanzato su apprendimento automatico e intelligenza artificiale con IIIT-B e Liverpool John Moores University.