Teorema di Bayes spiegato con l'esempio – Guida completa

introduzione

Che cos'è il teorema di Bayes?

Il teorema di Bayes viene utilizzato per il calcolo di una probabilità condizionata in cui l'intuizione spesso fallisce. Sebbene ampiamente utilizzato nella probabilità, il teorema viene applicato anche nel campo dell'apprendimento automatico. Il suo utilizzo nell'apprendimento automatico include l'adattamento di un modello a un set di dati di addestramento e lo sviluppo di modelli di classificazione.

Cos'è la probabilità condizionata?

Una probabilità condizionata è generalmente definita come la probabilità di un evento dato il verificarsi di un altro evento.

• Se A e B sono due eventi, allora la probabilità condizionata me è designata come P(A dato B) o P(A|B).
• La probabilità condizionata può essere calcolata dalla probabilità congiunta (A | B) = P(A, B) / P(B)

• La probabilità condizionata non è simmetrica; Ad esempio P(A | B) != P(B | A)

Altri modi per calcolare la probabilità condizionale includono l'uso dell'altra probabilità condizionale, ad es

P(A|B) = P(B|A) * P(A) / P(B)

Viene utilizzato anche il contrario

P(B|A) = P(A|B) * P(B) / P(A)

Questo metodo di calcolo è utile quando è difficile calcolare la probabilità congiunta. Altrimenti, quando è disponibile la probabilità condizionale inversa, il calcolo attraverso questo diventa facile.

Questo calcolo alternativo della probabilità condizionata è indicato come regola di Bayes o teorema di Bayes. Prende il nome dalla persona che per primo lo descrisse, "Reverendo Thomas Bayes".

La formula del teorema di Bayes

Il teorema di Bayes è un modo per calcolare la probabilità condizionata quando la probabilità congiunta non è disponibile. A volte, non è possibile accedere direttamente al denominatore. In tali casi, il metodo alternativo di calcolo è il seguente:

P(B) = P(B|A) * P(A) + P(B|non A) * P(non A)

Questa è la formulazione del teorema di Bayes che mostra un calcolo alternativo di P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|non A) * P(non A)

La formula sopra può essere descritta tra parentesi attorno al denominatore

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|non A) * P(non A))

Inoltre, se abbiamo P(A), allora P(non A) può essere calcolato come

P(non A) = 1 – P(A)

Allo stesso modo, se abbiamo P(non B|non A), allora P(B|non A) può essere calcolato come

P(B|non A) = 1 – P(non B|non A)

Teorema di Bayes della probabilità condizionata

Il teorema di Bayes è costituito da diversi termini i cui nomi sono dati in base al contesto della sua applicazione nell'equazione.

La probabilità a posteriori si riferisce al risultato di P(A|B) e la probabilità a priori si riferisce a P(A).

• P(A|B): Probabilità a posteriori.
• P(A): Probabilità a priori.

Allo stesso modo, P(B|A) e P(B) sono indicati come probabilità e evidenza.

• P(B|A): Probabilità.
• P(B): Prove.

Pertanto, il teorema di Bayes della probabilità condizionata può essere riformulato come:

Posteriore = Probabilità * Priore / Evidenza

Se dobbiamo calcolare la probabilità che ci sia fuoco dato che c'è fumo, allora verrà utilizzata la seguente equazione:

P(Fuoco|Fumo) = P(Fumo|Fuoco) * P(Fuoco) / P(Fumo)

Dove P(Fuoco) è il Priore, P(Fumo|Fuoco) è la Probabilità e P(Fumo) è l'evidenza.

Un'illustrazione del teorema di Bayes

Viene descritto un esempio di teorema di Bayes per illustrare l'uso del teorema di Bayes in un problema.

Problema

Sono presenti tre caselle etichettate come A, B e C. I dettagli delle scatole sono:

• La scatola A contiene 2 palline rosse e 3 nere
• La scatola B contiene 3 palline rosse e 1 nera
• E la scatola C contiene 1 pallina rossa e 4 palline nere

Tutte e tre le scatole sono identiche con uguale probabilità di essere ritirate. Quindi, qual è la probabilità che la pallina rossa sia stata prelevata dalla casella A?

Soluzione

Sia E l'evento in cui viene raccolta una pallina rossa e A, B e C denotano che la pallina viene prelevata dalle rispettive caselle. Pertanto la probabilità condizionata sarebbe P(A|E) che deve essere calcolata.

Le probabilità esistenti P(A) = P(B) = P (C) = 1 / 3, poiché tutte le caselle hanno la stessa probabilità di essere selezionate.

P(E|A) = Numero di palline rosse nella casella A / Numero totale di palline nella casella A = 2 / 5

Allo stesso modo, P(E|B) = 3 / 4 e P(E|C) = 1 / 5

Quindi evidenza P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Pertanto, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Esempio di teorema di Bayes

Il teorema di Bayes fornisce la probabilità di un "evento" con le informazioni fornite sui "test".

• C'è una differenza tra "eventi" e "prove". Per esempio c'è un test per la malattia del fegato, che è diverso dall'avere effettivamente la malattia del fegato, cioè un evento.
• Gli eventi rari potrebbero avere un tasso di falsi positivi più alto.

Esempio 1

Qual è la probabilità che un paziente abbia una malattia del fegato se è alcolizzato?

Qui, "essere alcolizzato" è il "test" (tipo di cartina di tornasole) per le malattie del fegato.

• A è l'evento cioè “il paziente ha una malattia del fegato””.

Come da precedenti documenti della clinica, si afferma che il 10% dei pazienti che entrano in clinica soffre di malattie del fegato.

Pertanto, P(A)=0,10

• B è la cartina di tornasole che “Il paziente è un alcolista”.

Le registrazioni precedenti della clinica hanno mostrato che il 5% dei pazienti che entrano nella clinica sono alcolisti.

Pertanto, P(B)=0,05

• Inoltre, il 7% dei pazienti a cui è stata diagnosticata una malattia del fegato sono alcolisti. Questo definisce il B|A: la probabilità che un paziente sia alcolizzato, dato che ha una malattia del fegato è del 7%.

Come, per la formula del teorema di Bayes ,

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Pertanto, per un paziente alcolizzato, le probabilità di avere una malattia del fegato sono 0,14 (14%).

Esempio2

• Gli incendi pericolosi sono rari (1%)
• Ma il fumo è abbastanza comune (10%) a causa dei barbecue,
• E il 90% degli incendi pericolosi produce fumo

Qual è la probabilità di un incendio pericoloso in presenza di fumo?

Calcolo

P(Fuoco|Fumo) =P(Fuoco) P(Fumo|Fuoco)/P(Fumo)

= 1% x 90%/10%

= 9%

Esempio 3

Qual è la possibilità di pioggia durante il giorno? Dove, Rain significa pioggia durante il giorno e Cloud significa mattina nuvolosa.

La possibilità di pioggia data da Cloud è scritta P(Rain|Cloud)

P(Pioggia|Nuvola) = P(Pioggia) P(Nuvola|Pioggia)/P(Nuvola)

P(Pioggia) è Probabilità di pioggia = 10%

P(Nuvola|Pioggia) è Probabilità di Nubi, dato che piove = 50%

P(Cloud) è Probabilità di Cloud = 40%

P(Pioggia|Nuvole) = 0,1 x 0,5/0,4 = 0,125

Pertanto, una probabilità di pioggia del 12,5%.

Applicazioni

Esistono diverse applicazioni del teorema di Bayes nel mondo reale. Le poche applicazioni principali del teorema sono:

1. Ipotesi di modellazione

Il teorema di Bayes trova ampia applicazione nell'apprendimento automatico applicato e stabilisce una relazione tra i dati e un modello. L'apprendimento automatico applicato utilizza il processo di test e analisi di diverse ipotesi su un determinato set di dati.

Per descrivere la relazione tra i dati e il modello, il teorema di Bayes fornisce un modello probabilistico.

P(h|D) = P(D|h) * P(h) / P(D)

Dove,

P(h|D): Probabilità a posteriori dell'ipotesi

P(h): probabilità a priori dell'ipotesi.

Un aumento di P(D) diminuisce il P(h|D). Al contrario, se P(h) e la probabilità di osservare l'ipotesi data aumentano, allora aumenta la probabilità di P(h|D).

2. Teorema di Bayes per la classificazione

Il metodo di classificazione prevede l'etichettatura di un dato dato. Può essere definito come il calcolo della probabilità condizionata di un'etichetta di classe data un campione di dati.

P(classe|dati) = (P(dati|classe) * P(classe)) / P(dati)

Dove P(classe|dati) è la probabilità della classe dati i dati forniti.

Il calcolo può essere effettuato per ogni classe. La classe con la probabilità maggiore può essere assegnata ai dati di input.

Il calcolo della probabilità condizionata non è fattibile in condizioni di un piccolo numero di esempi. Pertanto, l'applicazione diretta del teorema di Bayes non è fattibile. Una soluzione al modello di classificazione risiede nel calcolo semplificato.

• Classificatore ingenuo di Bayes

Il teorema di Bayes considera che le variabili di input dipendono da altre variabili che causano la complessità del calcolo. Pertanto, l'assunzione viene rimossa e ogni variabile di input viene considerata come una variabile indipendente. Di conseguenza, il modello cambia da modello di probabilità condizionale dipendente a modello di probabilità condizionale indipendente. Alla fine riduce la complessità.

Questa semplificazione del teorema di Bayes viene chiamata Naive Bayes. È ampiamente utilizzato per la classificazione e la previsione di modelli.

• Classificatore ottimale di Bayes

Questo è un tipo di modello probabilistico che prevede la previsione di un nuovo esempio dato il set di dati di addestramento. Un esempio del Bayes Optimal Classifier è "Qual è la classificazione più probabile della nuova istanza dati i dati di addestramento?"

Il calcolo della probabilità condizionata di una nuova istanza dati i dati di addestramento può essere effettuato tramite la seguente equazione

P(vj | D) = somma {h in H} P(vj | hi) * P(hi | D)

Dove vj è una nuova istanza da classificare,

H è l'insieme delle ipotesi per classificare l'istanza,

ciao è un'ipotesi data

P(vj | hi) è la probabilità a posteriori per vi data l'ipotesi hi, e

P(hi | D) è la probabilità a posteriori dell'ipotesi hi dati i dati D.

3. Usi del teorema di Bayes nell'apprendimento automatico

L'applicazione più comune del teorema di Bayes nell'apprendimento automatico è lo sviluppo di problemi di classificazione. Altre applicazioni anziché la classificazione includono l'ottimizzazione e i modelli casuali.

• Ottimizzazione bayesiana

È sempre un compito difficile trovare un input che si traduca nel costo minimo o massimo di una determinata funzione obiettivo. L'ottimizzazione bayesiana si basa sul teorema di Bayes e fornisce un aspetto per la ricerca di un problema di ottimizzazione globale. Il metodo prevede la costruzione di un modello probabilistico (funzione surrogata), la ricerca attraverso una funzione di acquisizione e la selezione di campioni candidati per la valutazione della funzione obiettivo reale.

Nell'apprendimento automatico applicato, l'ottimizzazione bayesiana viene utilizzata per ottimizzare gli iperparametri di un modello con buone prestazioni.

• Reti di credenze bayesiane

Le relazioni tra le variabili possono essere definite attraverso l'uso di modelli probabilistici. Sono utilizzati anche per il calcolo delle probabilità. Un modello di probabilità completamente condizionale potrebbe non essere in grado di calcolare le probabilità a causa dell'elevato volume di dati. Naive Bayes ha semplificato l'approccio per il calcolo. Esiste ancora un altro metodo in cui viene sviluppato un modello basato sulla nota dipendenza condizionale tra variabili casuali e indipendenza condizionale in altri casi. La rete bayesiana mostra questa dipendenza e indipendenza attraverso il modello di grafo probabilistico con bordi diretti. La dipendenza condizionale nota viene visualizzata come spigoli diretti e le connessioni mancanti rappresentano le dipendenze condizionali nel modello.

4. Filtraggio spam bayesiano

Il filtro antispam è un'altra applicazione del teorema di Bayes. Sono presenti due eventi:

• Evento A: il messaggio è spam.
• Test X: il messaggio contiene alcune parole (X)

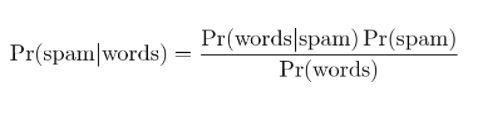
Con l'applicazione del teorema di Bayes si può prevedere se il messaggio è spam dati i “risultati del test”. L'analisi delle parole in un messaggio può calcolare le possibilità di essere un messaggio di spam. Con l'addestramento dei filtri con messaggi ripetuti, aggiorna il fatto che la probabilità di avere determinate parole nel messaggio sarebbe spam.

Un'applicazione del teorema di Bayes con un esempio

Un produttore di catalizzatori produce un dispositivo per testare i difetti in un determinato elettrocatalizzatore (EC). Il produttore del catalizzatore afferma che il test è affidabile al 97% se l'EC è difettoso e affidabile al 99% quando è impeccabile. Tuttavia, è possibile che il 4% di detto EC sia difettoso al momento della consegna. La regola di Bayes viene applicata per accertare la vera affidabilità del dispositivo. I set di eventi di base sono

R : il CE è difettoso; R': la CE è impeccabile; B: la CE è testata per essere difettosa; B': la CE è testata per essere impeccabile.

Le probabilità sarebbero

B/A: EC è (noto per essere) difettoso e testato difettoso, P(B/A) = 0,97,

B'/A: EC è (noto per essere) difettoso, ma testato senza difetti, P(B'/A)=1-P(B/A)=0,03,

B/A': EC è (noto per essere) difettoso, ma testato difettoso, P(B/A') = 1- P(B'/A')=0,01

B'/A: = EC è (noto per essere) impeccabile e testato impeccabile P(B'/A') = 0,99

Le probabilità calcolate dal teorema di Bayes sono:

La probabilità di calcolo mostra che esiste un'elevata possibilità di rifiutare EC impeccabili (circa 20%) e una bassa possibilità di identificare EC difettose (circa 80%).

Conclusione

Una delle caratteristiche più sorprendenti di un teorema di Bayes è che da pochi rapporti di probabilità si può ottenere un'enorme quantità di informazioni. Con i mezzi di verosimiglianza, la probabilità di un evento precedente può essere trasformata nella probabilità a posteriori. Gli approcci del teorema di Bayes possono essere applicati in aree di statistica, epistemologia e logica induttiva.

Se sei interessato a saperne di più sul teorema di Bayes, sull'intelligenza artificiale e sull'apprendimento automatico, dai un'occhiata al programma Executive PG di IIIT-B e upGrad in Machine Learning e AI, progettato per i professionisti che lavorano e offre oltre 450 ore di formazione rigorosa, oltre 30 casi studi e incarichi, stato di Alumni IIIT-B, oltre 5 progetti pratici pratici e assistenza sul lavoro con le migliori aziende.