Apa itu Pemikiran Bayesian? Pendahuluan dan Teorema

Sebuah teorema statistik yang diberikan oleh ahli statistik dan filsuf Inggris Thomas Bayes pada tahun 1700-an terus menjadi cahaya penuntun bagi para ilmuwan dan analis di seluruh dunia. Hari ini, pemikiran Bayesian menemukan aplikasi dalam kedokteran, sains, teknologi, dan beberapa disiplin ilmu lainnya dan terus mempengaruhi pandangan dunia kita dan tindakan yang dihasilkan dengan kuat.

Ide Thomas Bayes sangat sederhana. Menurut Bayes, probabilitas suatu hipotesis menjadi benar bergantung pada dua kondisi: seberapa masuk akal hipotesis itu didasarkan pada apa yang sudah kita ketahui (pengetahuan sebelumnya) dan seberapa cocok hipotesis itu dengan bukti baru. Dengan demikian, pemikiran Bayesian berbeda dari pengujian hipotesis tradisional di mana yang pertama mencakup pengetahuan sebelumnya sebelum melompat ke kesimpulan.

Dengan pengenalan pendahuluan, mari kita selami lebih detail tentang statistik Bayesian.

Statistik Bayesian

Secara sederhana, statistik Bayesian menerapkan probabilitas pada masalah statistik untuk memperbarui keyakinan sebelumnya berdasarkan bukti data baru. Probabilitas mengungkapkan tingkat kepercayaan dalam peristiwa tertentu.

Tingkat kepercayaan mungkin didasarkan pada pengetahuan sebelumnya tentang peristiwa tersebut berdasarkan asumsi pribadi atau hasil eksperimen sebelumnya. Statistik Bayesian menggunakan Teorema Bayes untuk menghitung probabilitas. Teorema Bayes, pada gilirannya, menggambarkan probabilitas bersyarat dari suatu peristiwa berdasarkan bukti baru dan informasi sebelumnya yang terkait dengan peristiwa tersebut.

Dengan mengingat hal itu, mari kita memoles konsep dasar probabilitas bersyarat sebelum kita memahami Teorema Bayes secara mendalam.

Probabilitas Bersyarat

Probabilitas bersyarat dapat didefinisikan sebagai kemungkinan suatu peristiwa atau hasil berdasarkan terjadinya peristiwa atau hasil sebelumnya. Ini dihitung dengan mengalikan probabilitas kejadian sebelumnya dengan probabilitas kejadian berikutnya atau kondisional.

Mari kita lihat contoh untuk memahami konsep dengan lebih baik .

• Acara A adalah keluarga berencana jalan-jalan akan pergi piknik. Ada kemungkinan 80% bahwa keluarga akan pergi piknik.
• Peristiwa B adalah akan turun hujan pada hari keluarga pergi piknik. Prakiraan cuaca mengatakan bahwa ada kemungkinan 60% curah hujan pada hari piknik.
• Oleh karena itu, peluang (P) bahwa keluarga tersebut pergi piknik dan hujan turun dihitung sebagai berikut:

P (Piknik dan hujan) = P (Hujan | Piknik) P (Piknik) = (0.60) * (0.80) = 0.48

Dalam contoh di atas, peluang bersyarat melihat dua peristiwa A dan B dalam hubungan satu sama lain, yaitu, peluang bahwa keluarga pergi piknik dan juga hujan pada hari yang sama.

Oleh karena itu, probabilitas bersyarat berbeda dari probabilitas tak bersyarat karena yang terakhir mengacu pada kemungkinan terjadinya suatu peristiwa terlepas dari apakah peristiwa atau peristiwa lain telah terjadi atau kondisi lain ada.

Rumus untuk probabilitas bersyarat

Rumus untuk probabilitas bersyarat berasal dari aturan perkalian probabilitas:

P (A dan B) atau P (AUB) = P ( B diberikan A) atau P (B | A) * P (A)

Dalam persamaan di atas, P (A dan B) adalah probabilitas bersama, mengacu pada kemungkinan dua atau lebih peristiwa yang terjadi secara bersamaan. Hal ini juga ditulis sebagai P (A,B).

Berikut cara menyimpulkan persamaan probabilitas bersyarat dari aturan perkalian:

Langkah 1: Tuliskan aturan perkalian.

P (A dan B) = P (B | A) * P (A)

Langkah 2: Bagi kedua ruas persamaan dengan P (A).

P (A dan B) / P (A) = P (B | A) * P (A) / P (A)

Langkah 3: Batalkan P (A) pada ruas kanan persamaan.

P (A dan B) / P (A) = P (B | A)

Langkah 4: Tulis ulang persamaan.

P (A dan B) = P (B | A) / P (A)

Dengan demikian, rumus untuk probabilitas bersyarat diberikan sebagai:

P (A dan B) = P (B | A) / P (A)

Teorema Bayes

Dengan menggunakan Teorema Bayes, kita dapat memperbarui keyakinan dan keyakinan kita berdasarkan bukti baru dan relevan. Misalnya, jika kita mencoba mencari tahu kemungkinan seseorang terkena kanker, kita umumnya akan menganggapnya sebagai persentase dari populasi yang menderita kanker. Namun, jika kita memperkenalkan bukti tambahan, seperti orang tersebut adalah perokok biasa, kita dapat memperbarui persepsi kita (dan karenanya kemungkinan) karena kemungkinan menderita kanker lebih tinggi jika seseorang adalah perokok. Oleh karena itu, kami menggunakan pengetahuan kami sebelumnya dan bukti tambahan untuk meningkatkan estimasi kami.

Rumus Teorema Bayes

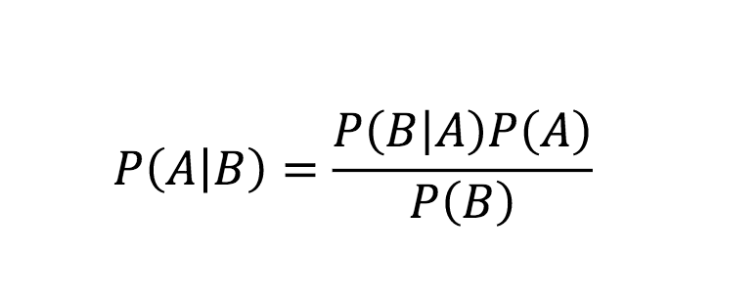
Sumber

Persamaan di atas adalah aturan Bayes. Sekarang, mari kita lihat turunan bertahap dari persamaan Teorema Bayes.

Langkah 1: Pertimbangkan dua kejadian, A dan B. A adalah kejadian yang probabilitasnya ingin kita hitung dan B adalah bukti tambahan yang terkait dengan A.

Langkah 2: Tuliskan hubungan antara peluang gabungan dan peluang bersyarat dari kejadian A dan B.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Langkah 3: Tetapkan dua istilah probabilitas bersyarat yang sama satu sama lain.

P (A | B) * P(B) = P (B | A) * P(A)

Langkah 4: Bagi kedua ruas persamaan dengan P (B).

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

Langkah 5: Batalkan P (B) di sisi kiri persamaan.

P (A | B) = P (B | A) * P(A) / P (B)

Dengan demikian, kita mendapatkan rumus Teorema Bayes sebagai berikut:

P (A | B) = P (B | A) * P(A) / P (B)

Memahami istilah dalam persamaan Teorema Bayes

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) disebut probabilitas posterior atau probabilitas yang kita coba perkirakan. Berdasarkan contoh sebelumnya, probabilitas posterior adalah probabilitas orang tersebut menderita kanker, mengingat orang tersebut adalah perokok biasa.
• P (B | A) disebut kemungkinan , mengacu pada kemungkinan mendeteksi bukti tambahan, mengingat hipotesis awal kami. Dalam contoh di atas, kemungkinannya adalah kemungkinan orang tersebut menjadi perokok, mengingat orang tersebut menderita kanker.
• P (A) adalah probabilitas sebelumnya atau probabilitas hipotesis kami tanpa bukti atau informasi tambahan. Dalam contoh di atas, probabilitas sebelumnya adalah probabilitas menderita kanker.
• P (B) adalah kemungkinan marjinal atau probabilitas total mengamati bukti. Dalam konteks contoh di atas, kemungkinan marjinal adalah kemungkinan menjadi perokok.

Contoh Sederhana Untuk Memahami Teorema Bayes

Dengan menggunakan beberapa bilangan hipotetis pada contoh sebelumnya, kita akan melihat efek penerapan Teorema Bayes.

Misalkan probabilitas menderita kanker adalah 0,06, yaitu 6% orang menderita kanker. Sekarang, katakanlah bahwa peluang menjadi perokok adalah 0,20 atau 20% orang adalah perokok, dan 30% penderita kanker adalah perokok. Jadi, P (Perokok | Kanker) = 0,30.

Awalnya, kemungkinan terkena kanker hanya 0,06 (sebelumnya). Tetapi dengan menggunakan bukti baru, kita dapat menghitung P (Kanker | Perokok) = P ((Perokok | Kanker) * P (Kanker)) / P (Perokok) = (0,30*0,06) / (0,20) = 0,09.

Pelajari kursus ilmu data online dari Universitas top dunia. Dapatkan Program PG Eksekutif, Program Sertifikat Tingkat Lanjut, atau Program Magister untuk mempercepat karier Anda.

Langkah ke Depan: Kuasai Konsep Statistik untuk Berkarir di Ilmu Data atau Pembelajaran Mesin

Platform pembelajaran EdTech upGrad yang lebih tinggi telah memengaruhi lebih dari 500.000 profesional yang bekerja di seluruh dunia dengan sejumlah besar kursus dan pengalaman belajar yang imersif. Dengan 40.000+ basis pelajar yang tersebar di 85+ negara, kursus upGrad yang relevan dengan industri dijamin akan memajukan karir Anda di bidang pilihan Anda.

Master of Science dalam Ilmu Data adalah kursus 18 bulan yang memberikan keterampilan utama dalam Statistik, Analisis Prediktif, Pembelajaran Mesin, Analisis Data Besar, Visualisasi Data, dll.

Sorotan Program:

• Gelar Master dari Liverpool John Moores University dan Executive PGP dari IIIT Bangalore
• 500+ jam konten, 60+ studi kasus dan proyek, 20+ sesi langsung, 14+ bahasa dan alat pemrograman
• Jaringan industri, sesi penyelesaian keraguan, dan dukungan pembelajaran

Program Sertifikat Tingkat Lanjut dalam Pembelajaran Mesin dan Pembelajaran Mendalam adalah kursus 6 bulan yang ketat dengan peluang jaringan rekan, proyek langsung, bimbingan industri, dan bantuan karir 360 derajat.

Sorotan Program:

• Pengakuan bergengsi dari IIIT Bangalore
• 240+ jam konten, 5+ studi kasus, dan proyek, 24+ sesi langsung, cakupan 12 bahasa pemrograman, alat, dan perpustakaan
• Sesi pelatihan kelompok 1:8 dan sesi bimbingan 1:1 dengan pakar industri

Kesimpulan

Pemikiran Bayesian menopang beberapa bidang pemikiran, penyelidikan, dan kepercayaan manusia, meskipun kebanyakan dari kita tidak menyadarinya. Dari skrining kanker dan pemanasan global hingga kebijakan moneter dan penilaian risiko dan asuransi , pemikiran Bayesian sangat mendasar. Bahkan matematikawan Inggris terkenal Alan Turing diyakini telah menggunakan pendekatan Bayesian untuk memecahkan Kode Enigma Jerman selama Perang Dunia Kedua.

Daftar dengan upGrad dan tingkatkan pengetahuan Anda tentang konsep statistik utama dan banyak lagi!