Memulai Dengan Regresi Binomial Negatif: Panduan Langkah demi Langkah

Diterbitkan: 2022-04-17

Teknik Regresi Binomial Negatif digunakan untuk melakukan pemodelan variabel hitung. Metodenya hampir mirip dengan metode regresi berganda. Namun, terdapat perbedaan bahwa dalam kasus Regresi Binomial Negatif, variabel dependen, yaitu Y, mengikuti distribusi binomial negatif. Oleh karena itu, nilai variabel dapat berupa bilangan bulat non-negatif seperti 0, 1, 2.

Metode ini juga merupakan perluasan dari regresi Poisson yang membuat relaksasi dalam asumsi bahwa mean sama dengan varians. Salah satu model tradisional regresi binomial, yang didefinisikan sebagai "NB2," didasarkan pada distribusi campuran Poisson-gamma.

Metode regresi Poisson digeneralisasikan melalui penambahan variabel gamma noise. Variabel ini memiliki nilai mean satu dan juga parameter skala yaitu “v”.

Berikut adalah beberapa contoh Regresi Binomial Negatif:

Pihak sekolah melakukan penelitian untuk mempelajari perilaku kehadiran siswa SMA dari dua sekolah tersebut. Faktor-faktor yang mungkin mempengaruhi perilaku kehadiran mungkin termasuk hari-hari di mana yunior tidak hadir di sekolah. Juga, program di mana mereka terdaftar.
Seorang peneliti dari studi terkait kesehatan melakukan studi tentang berapa banyak warga lanjut usia yang mengunjungi rumah sakit dalam 12 bulan terakhir. Studi ini didasarkan pada karakteristik individu dan rencana kesehatan yang dibeli oleh para lansia.

Daftar isi

Contoh Regresi Binomial Negatif

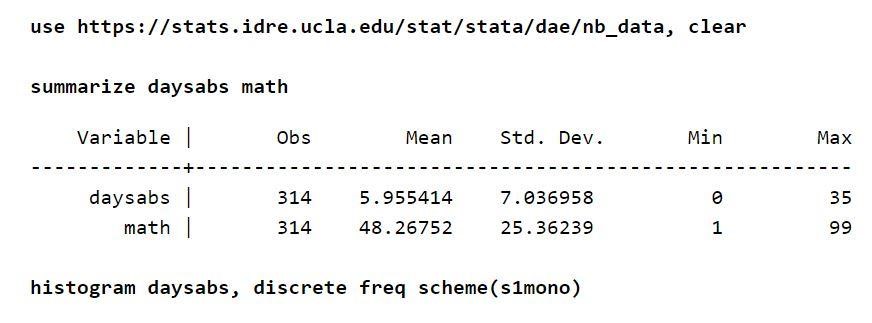
Misalkan ada lembar absensi sekitar 314 siswa dari SMA. Data diambil dari dua sekolah perkotaan dan disimpan dalam file bernama nb_data.dta. Variabel respon yang menarik dalam contoh ini adalah hari-hari absen yang disebut “daysabs”. Satu variabel, "matematika," hadir, yang mendefinisikan skor matematika untuk setiap siswa. Ada variabel lain yaitu "prog." Variabel ini menunjukkan program di mana siswa terdaftar.

Sumber

Masing-masing variabel memiliki sekitar 314 observasi. Oleh karena itu, distribusi antar variabel juga masuk akal. Juga, mengingat variabel hasil, mean tak bersyarat lebih rendah dari varians.

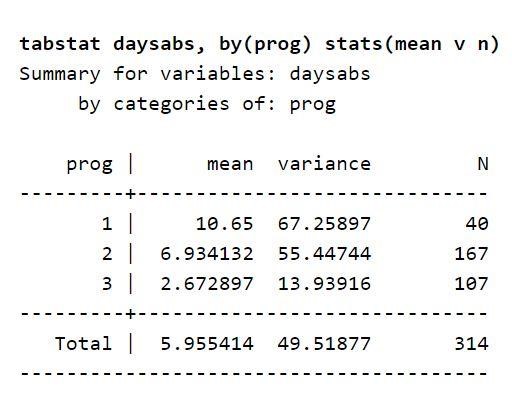
Sekarang, fokus pada deskripsi variabel yang dipertimbangkan dalam dataset. Sebuah tabel mentabulasi hari rata-rata seorang siswa tidak masuk sekolah di setiap jenis program. Hal ini menunjukkan bahwa variabel jenis program dapat memprediksi hari-hari siswa tidak masuk sekolah. Anda juga dapat menggunakannya untuk memprediksi variabel hasil. Hal ini karena nilai rata-rata untuk variabel hasil bervariasi dengan variabel prog. Juga, nilai varians lebih tinggi daripada di setiap tingkat prog variabel. Nilai-nilai ini disebut varians dan mean. Perbedaan yang ada menunjukkan adanya over-dispersi, dan oleh karena itu akan tepat untuk menggunakan model binomial negatif.

Sumber

Seorang peneliti dapat mempertimbangkan beberapa metode analisis untuk jenis penelitian ini. Metode-metode ini dijelaskan di bawah ini. Beberapa metode analisis yang dapat digunakan pengguna untuk menganalisis model regresi adalah:

1. Regresi binomial negatif

Metode Regresi Binomial Negatif digunakan ketika ada data yang tersebar berlebihan. Artinya nilai conditional variance lebih tinggi atau melebihi nilai conditional mean. Metode tersebut dianggap digeneralisasikan dari metode regresi Poisson. Hal ini dikarenakan kedua metode tersebut memiliki struktur mean yang sama. Namun, ada parameter tambahan dalam regresi binomial negatif yang digunakan untuk memodelkan overdispersi. Interval kepercayaan dianggap lebih sempit daripada regresi gairah ketika distribusi bersyarat terlalu tersebar dari variabel hasil.

2. Regresi Poisson

Metode regresi Poisson digunakan dalam pemodelan data hitung. Banyak ekstensi dapat digunakan untuk memodelkan variabel hitungan dalam regresi Poisson.

3. Regresi OLS

Hasil dari variabel hitungan kadang-kadang ditransformasi log dan kemudian dianalisis melalui metode regresi OLS. Namun, terkadang ada masalah yang terkait dengan metode regresi OLS. Masalah ini mungkin berupa hilangnya data karena menghasilkan nilai yang tidak ditentukan melalui pertimbangan log nilai nol. Juga, mungkin dihasilkan karena kurangnya pemodelan data yang tersebar.

4. Model nol-meningkat

Jenis model ini mencoba memperhitungkan semua kelebihan nol dalam model.

Analisis Menggunakan Regresi Binomial Negatif

Perintah “nbreg” digunakan untuk mengestimasi model Regresi Binomial Negatif. Ada "i" sebelum variabel "prog." Adanya “i” menunjukkan bahwa variabel tersebut bertipe faktor, yaitu variabel kategorik. Ini harus dimasukkan sebagai variabel indikator dalam model.

Keluaran model dimulai dengan log iterasi. Itu dimulai melalui pemasangan model Poisson, diikuti oleh model nol, dan kemudian model binomial negatif. Metode ini menggunakan estimasi kemungkinan maksimum dan terus melakukan iterasi sampai terjadi perubahan nilai log akhir. Kemungkinan log digunakan untuk perbandingan model.
Informasi selanjutnya ada di file header.
Ada informasi koefisien Regresi Binomial Negatif tepat di bawah header. Koefisien yang dihasilkan untuk setiap variabel bersama dengan kesalahan seperti nilai-p, nilai-z. Ada juga interval kepercayaan 95% untuk semua koefisien. Koefisien untuk variabel “matematika” adalah -0,006, yang menunjukkan bahwa variabel tersebut signifikan secara statistik. Hasilnya berarti bahwa jika ada peningkatan satu unit pada variabel “matematika”, jumlah log yang diharapkan untuk jumlah hari tidak hadir berkurang dengan nilai 0,006. Juga, nilai 2. prog, variabel indikator, adalah perbedaan yang diharapkan dalam hitungan log antara kedua kelompok ( kelompok 2 dan kelompok referensi).
Estimasi parameter untuk dispersi lebih dari log yang ditransfer dilakukan dan kemudian ditampilkan dengan nilai yang tidak diubah. Dalam model Poisson, nilainya adalah nol.
Ada informasi kemungkinan uji rasio di bawah tabel koefisien. Model dapat dipahami lebih lanjut melalui penggunaan perintah "margin."

Proses Melakukan Analisis Regresi Binomial Negatif dengan Python

Paket yang diperlukan untuk melakukan proses regresi harus diimpor dari Python. Paket-paket ini tercantum di bawah ini:

impor statsmodels.api sebagai sm
impor matplotlib.pyplot sebagai plt
impor numpy sebagai np
dari dmatrices impor patty
impor panda sebagai pd

Pertimbangan untuk Regresi Binomial Negatif

Ada beberapa hal yang harus diperhatikan dalam menerapkan metode analisis Regresi Binomial Negatif. Ini termasuk:

Jika terdapat sampel yang kecil, maka metode Regresi Binomial Negatif tidak direkomendasikan.
Terkadang ada kelebihan nol yang mungkin menjadi penyebab overdispersi. Angka nol ini mungkin dihasilkan karena proses penambahan pembuatan data. Jika jenis kasus seperti itu terjadi, disarankan untuk menggunakan metode model zero-inflated.
Jika proses pembuatan data tidak mempertimbangkan nol, maka dalam kasus seperti itu, disarankan untuk menggunakan metode model terpotong nol.
Ada variabel eksposur yang terkait dengan jumlah data. Variabel menunjukkan waktu ada kemungkinan peristiwa itu dapat terjadi. Variabel ini perlu dimasukkan ke dalam model Regresi Binomial Negatif. Ini dilakukan melalui opsi exp().
Variabel hasil tidak boleh bernilai negatif dalam model analisis Regresi Binomial Negatif. Juga, variabel eksposur tidak dapat memiliki nilai 0.
Perintah “glm” juga dapat digunakan untuk menjalankan metode analisis Regresi Binomial Negatif. Ini dapat dilakukan melalui tautan log dan juga keluarga binomial.
Perintah "glm" diperlukan untuk mendapatkan residu. Hal ini untuk memeriksa apakah ada asumsi lain dalam model Regresi Binomial Negatif.
Adanya berbagai ukuran pseudo-R-squared. Namun, setiap ukuran memberikan informasi yang mirip dengan informasi yang diberikan oleh R-kuadrat dalam regresi OLS.

Kesimpulan

Artikel tersebut membahas topik Regresi Binomial Negatif . Kita telah melihat bahwa ini hampir mirip dengan metode regresi berganda dan merupakan bentuk umum dari distribusi Poisson. Ada beberapa aplikasi dari metode ini. Teknik tersebut juga dapat diterapkan melalui bahasa pemrograman python atau dalam bahasa R.

Beberapa studi kasus juga hadir yang menunjukkan penerapannya dalam studi seperti penuaan. Selain itu, model regresi klasik yang dapat digunakan pada data hitung adalah Regresi Poisson, Regresi Binomial Negatif, dan Regresi Geometris. Metode-metode ini termasuk dalam keluarga model linier dan disertakan dalam hampir semua paket statistik seperti sistem R.

Jika Anda ingin unggul dalam pembelajaran mesin dan ingin menjelajahi bidang data, maka Anda dapat memeriksa kursus Program PG Eksekutif dalam Pembelajaran Mesin & AI yang ditawarkan oleh upGrad. Jadi, jika Anda seorang profesional yang bekerja yang bercita-cita menjadi ahli dalam pembelajaran mesin, datang dan dapatkan pengalaman dilatih di bawah para ahli. Rincian lebih lanjut dapat dicapai melalui website kami. Untuk setiap pertanyaan, tim kami dapat membantu Anda segera.

Ingin berbagi artikel ini?

Tingkatkan Karir Anda dalam Pembelajaran Mesin dan Kecerdasan Buatan

Daftar Sekarang untuk Sertifikasi Eksekutif di Ai-ml dari IIITB