Gaussian Naive Bayes: Apa yang Perlu Anda Ketahui?
Diterbitkan: 2021-02-22Daftar isi
Gaussian Naive Bayes
Naive Bayes adalah algoritma pembelajaran mesin probabilistik yang digunakan untuk banyak fungsi klasifikasi dan didasarkan pada teorema Bayes. Gaussian Naive Bayes adalah perpanjangan dari Naive Bayes. Sementara fungsi lain digunakan untuk memperkirakan distribusi data, Gaussian atau distribusi normal adalah yang paling sederhana untuk diterapkan karena Anda perlu menghitung mean dan standar deviasi untuk data pelatihan.
Apa itu Algoritma Naive Bayes?
Naive Bayes adalah algoritma pembelajaran mesin probabilistik yang dapat digunakan dalam beberapa tugas klasifikasi. Aplikasi khas Naive Bayes adalah klasifikasi dokumen, penyaringan spam, prediksi dan sebagainya. Algoritma ini didasarkan pada penemuan Thomas Bayes dan karenanya namanya.
Nama "Naive" digunakan karena algoritma menggabungkan fitur dalam modelnya yang independen satu sama lain. Setiap modifikasi dalam nilai satu fitur tidak secara langsung berdampak pada nilai fitur lain dari algoritme. Keuntungan utama dari algoritma Naive Bayes adalah bahwa itu adalah algoritma yang sederhana namun kuat.
Ini didasarkan pada model probabilistik di mana algoritma dapat dikodekan dengan mudah, dan prediksi dilakukan dengan cepat secara real-time. Oleh karena itu, algoritme ini adalah pilihan umum untuk memecahkan masalah dunia nyata karena dapat disesuaikan untuk merespons permintaan pengguna secara instan. Namun sebelum kita menyelam jauh ke dalam Naive Bayes dan Gaussian Naive Bayes, kita harus mengetahui apa yang dimaksud dengan probabilitas bersyarat.
Probabilitas Bersyarat Dijelaskan
Kita dapat memahami probabilitas bersyarat lebih baik dengan sebuah contoh. Saat Anda melempar koin, kemungkinan maju atau tertinggal adalah 50%. Demikian pula, peluang mendapatkan 4 saat Anda melempar dadu dengan wajah adalah 1/6 atau 0,16.
Jika kita mengambil satu pak kartu, berapa peluang mendapatkan ratu dengan syarat kartu itu sekop? Karena kondisinya sudah ditetapkan sehingga harus berupa sekop, penyebut atau himpunan pilihannya menjadi 13. Hanya ada satu ratu dalam sekop, maka peluang terambilnya ratu sekop menjadi 1/13= 0,07.

Probabilitas bersyarat dari kejadian A kejadian B berarti probabilitas kejadian A jika kejadian B telah terjadi. Secara matematis, probabilitas bersyarat dari A B yang diberikan dapat dilambangkan sebagai P[A|B] = P[A AND B] / P[B].
Mari kita perhatikan contoh yang sedikit rumit. Ambil sekolah dengan total 100 siswa. Populasi ini dapat dibagi menjadi 4 kategori- Siswa, Guru, Pria dan Wanita. Perhatikan tabulasi yang diberikan di bawah ini:
| Perempuan | Pria | Total | |
| Guru | 8 | 12 | 20 |
| Murid | 32 | 48 | 80 |
| Total | 40 | 50 | 100 |
Di sini, berapakah peluang bersyarat bahwa seorang penduduk sekolah tertentu adalah seorang Guru dengan syarat bahwa dia adalah seorang Laki-laki.
Untuk menghitung ini, Anda harus menyaring sub-populasi dari 60 pria dan menelusuri 12 guru pria.
Jadi, peluang bersyarat yang diharapkan P[Guru | Pria] = 12/60 = 0,2
P (Guru | Pria) = P (Guru Pria) / P (Pria) = 12/60 = 0,2
Ini dapat direpresentasikan sebagai Guru(A) dan Pria(B) dibagi dengan Pria(B). Demikian pula, probabilitas bersyarat dari B yang diberikan A juga dapat dihitung. Aturan yang kita gunakan untuk Naive Bayes dapat disimpulkan dari notasi berikut:
P (A | B) = P (A B) / P(B)
P (B | A) = P (A B) / P(A)
Aturan Bayes
Dalam aturan Bayes, kita pergi dari P (X | Y) yang dapat ditemukan dari dataset pelatihan untuk menemukan P (Y | X). Untuk mencapai ini, yang perlu Anda lakukan hanyalah mengganti A dan B dengan X dan Y dalam rumus di atas. Untuk observasi, X akan menjadi variabel yang diketahui dan Y akan menjadi variabel yang tidak diketahui. Untuk setiap baris dataset, Anda harus menghitung probabilitas Y mengingat X telah terjadi.
Tapi apa yang terjadi jika ada lebih dari 2 kategori di Y? Kita harus menghitung probabilitas setiap kelas Y untuk menemukan yang menang.
Melalui aturan Bayes, kita pergi dari P (X | Y) untuk menemukan P (Y | X)
Diketahui dari data latih: P (X | Y) = P (X Y) / P(Y)
P (Bukti | Hasil)
Tidak diketahui – diprediksi untuk data uji: P (Y | X) = P (X Y) / P(X)

P (Hasil | Bukti)
Aturan Bayes = P (Y | X) = P (X | Y) * P (Y) / P (X)
Bayes yang Naif
Aturan Bayes memberikan rumus untuk probabilitas Y yang diberikan kondisi X. Tetapi di dunia nyata, mungkin ada beberapa variabel X. Ketika Anda memiliki fitur independen, aturan Bayes dapat diperluas ke aturan Naive Bayes. X adalah independen satu sama lain. Rumus Naive Bayes lebih kuat dari rumus Bayes
Gaussian Naive Bayes
Sejauh ini, kita telah melihat bahwa X berada dalam kategori tetapi bagaimana menghitung probabilitas ketika X adalah variabel kontinu? Jika kita berasumsi bahwa X mengikuti distribusi tertentu, Anda dapat menggunakan fungsi kepadatan probabilitas dari distribusi tersebut untuk menghitung probabilitas kemungkinan.
Jika kita berasumsi bahwa X mengikuti distribusi Gaussian atau normal, kita harus mengganti kerapatan probabilitas dari distribusi normal dan menamakannya Gaussian Naive Bayes. Untuk menghitung rumus ini, Anda memerlukan mean dan varians dari X.
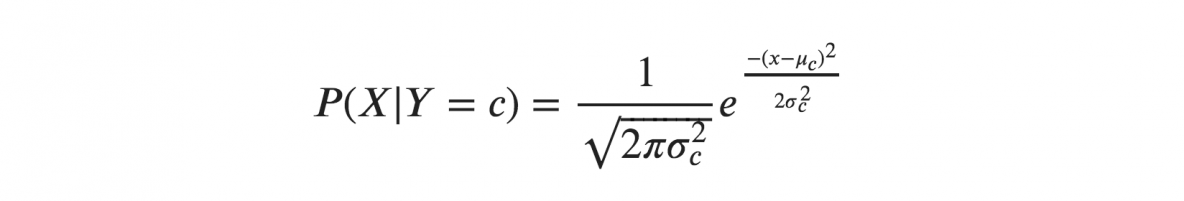
Dalam rumus di atas, sigma dan mu adalah varians dan mean dari variabel kontinu X yang dihitung untuk kelas c tertentu dari Y.
Representasi untuk Gaussian Naive Bayes
Rumus di atas menghitung probabilitas untuk nilai input untuk setiap kelas melalui frekuensi. Kita dapat menghitung mean dan standar deviasi dari x untuk setiap kelas untuk seluruh distribusi.
Ini berarti bahwa bersama dengan probabilitas untuk setiap kelas, kita juga harus menyimpan mean dan standar deviasi untuk setiap variabel input untuk kelas tersebut.
rata-rata(x) = 1/n * jumlah(x)
di mana n mewakili jumlah instance dan x adalah nilai variabel input dalam data.
simpangan baku(x) = kuadrat(1/n * jumlah(xi-mean(x)^2 ))
Di sini akar kuadrat dari rata-rata perbedaan setiap x dan rata-rata x dihitung di mana n adalah jumlah instance, sum() adalah fungsi penjumlahan, kuadrat() adalah fungsi akar kuadrat, dan xi adalah nilai x spesifik .

Prediksi dengan Model Gaussian Naive Bayes
Fungsi kepadatan probabilitas Gaussian dapat digunakan untuk membuat prediksi dengan mengganti parameter dengan nilai input baru dari variabel dan sebagai hasilnya, fungsi Gaussian akan memberikan perkiraan untuk probabilitas nilai input baru.
Pengklasifikasi Naive Bayes
Pengklasifikasi Naive Bayes mengasumsikan bahwa nilai satu fitur tidak tergantung pada nilai fitur lainnya. Pengklasifikasi Naive Bayes membutuhkan data pelatihan untuk memperkirakan parameter yang diperlukan untuk klasifikasi. Karena desain dan aplikasi yang sederhana, pengklasifikasi Naive Bayes dapat cocok di banyak skenario kehidupan nyata.
Kesimpulan
Pengklasifikasi Gaussian Naive Bayes adalah teknik pengklasifikasi cepat dan sederhana yang bekerja sangat baik tanpa terlalu banyak usaha dan tingkat akurasi yang baik.
Jika Anda tertarik untuk mempelajari lebih lanjut tentang AI, pembelajaran mesin, lihat PG Diploma IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk para profesional yang bekerja dan menawarkan 450+ jam pelatihan ketat, 30+ studi kasus & tugas, Status Alumni IIIT-B, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.
Pelajari Kursus ML dari Universitas top Dunia. Dapatkan Master, PGP Eksekutif, atau Program Sertifikat Tingkat Lanjut untuk mempercepat karier Anda.
Apa itu algoritma naive bayes?
Naive bayes adalah algoritma pembelajaran mesin klasik. Berasal dari statistik, naive bayes adalah algoritma yang sederhana dan kuat. Naive bayes adalah keluarga pengklasifikasi berdasarkan penerapan analisis probabilitas bersyarat. Dalam analisis ini, probabilitas bersyarat dari suatu peristiwa dihitung dengan menggunakan probabilitas masing-masing peristiwa individu yang membentuk peristiwa tersebut. Pengklasifikasi bayes naif sering ditemukan sangat efektif dalam praktiknya, terutama ketika jumlah dimensi set fitur besar.
Apa aplikasi dari algoritma naive bayes?
Naive Bayes digunakan dalam klasifikasi teks, klasifikasi dokumen dan untuk pengindeksan dokumen. Dalam naive bayes, setiap fitur yang mungkin tidak memiliki bobot yang ditetapkan dalam fase pra-pemrosesan dan bobot tersebut kemudian ditetapkan selama fase pelatihan serta pengenalan. Asumsi dasar dari algoritma naive bayes adalah bahwa fitur bersifat independen.
Apa itu algoritma Gaussian Naive Bayes?
Gaussian Naive Bayes adalah algoritma klasifikasi probabilistik berdasarkan penerapan teorema Bayes dengan asumsi independensi yang kuat. Dalam konteks klasifikasi, independensi mengacu pada gagasan bahwa kehadiran satu nilai fitur tidak mempengaruhi keberadaan yang lain (tidak seperti independensi dalam teori probabilitas). Naif mengacu pada penggunaan asumsi bahwa fitur suatu objek tidak tergantung satu sama lain. Dalam konteks pembelajaran mesin, pengklasifikasi naif Bayes dikenal sangat ekspresif, terukur, dan cukup akurat, tetapi kinerjanya memburuk dengan cepat seiring dengan pertumbuhan set pelatihan. Sejumlah fitur berkontribusi pada keberhasilan pengklasifikasi Bayes naif. Terutama, mereka tidak memerlukan penyetelan parameter model klasifikasi, mereka menskalakan dengan baik dengan ukuran kumpulan data pelatihan, dan mereka dapat dengan mudah menangani fitur berkelanjutan.
