Statistik dan Model Bayesian: Dijelaskan

Teknik Bayesian adalah pendekatan dalam statistik yang digunakan dalam analisis data dan estimasi parameter. Pendekatan ini didasarkan pada teorema Bayes.

Statistik Bayesian mengikuti prinsip unik yang membantu menentukan distribusi probabilitas gabungan untuk parameter yang diamati dan tidak diamati menggunakan model statistik. Pengetahuan statistik sangat penting untuk mengatasi masalah analitis dalam skenario ini.

Sejak diperkenalkannya teorema Bayes pada tahun 1770-an oleh Thomas Bayes, teorema ini tetap menjadi alat yang sangat diperlukan dalam statistik. Model Bayesian adalah pengganti klasik untuk model frequentist karena inovasi terbaru dalam statistik telah membantu menembus pencapaian di berbagai industri, termasuk penelitian medis, memahami pencarian web, dan memproses bahasa alami (Natural Language Processing).

Misalnya, Alzheimer adalah penyakit yang diketahui menimbulkan risiko progresif seiring bertambahnya usia seseorang. Namun, dengan bantuan teorema Bayes, dokter dapat memperkirakan kemungkinan seseorang menderita Alzheimer di masa depan. Ini juga berlaku untuk kanker dan penyakit terkait usia lainnya yang membuat seseorang menjadi rentan di tahun-tahun terakhir hidupnya.

Statistik Sering Vs Statistik Bayesian

Statistik Sering vs Statistik Bayesian secara konsisten menjadi topik kontroversi dan mimpi buruk bagi pemula, keduanya mengalami kesulitan memilih di antara keduanya. Pada awal abad ke-20, statistik Bayesian mengalami masalah ketidakpercayaan dan penerimaan. Namun, seiring berjalannya waktu, orang-orang menyadari penerapan model Bayesian dan solusi akurat yang dihasilkannya.

Berikut ini melihat statistik yang sering terjadi dan kerumitan yang terkait dengannya:

Statistik Sering

Ini adalah metodologi inferensial yang banyak digunakan dalam dunia statistik. Ini menganalisis apakah suatu peristiwa (disebutkan sebagai hipotesis) telah terjadi atau tidak. Ini juga memperkirakan kemungkinan peristiwa yang terjadi selama rentang percobaan. Percobaan diulang sampai hasil yang diinginkan tercapai.

Sampel distribusi mereka berukuran sebenarnya, dan eksperimen ini diulangi berkali-kali secara teoritis. Berikut adalah contoh yang menunjukkan seberapa sering statistik dapat digunakan untuk mempelajari pelemparan koin.

• Peluang untuk mendapatkan keuntungan pada pelemparan koin satu kali adalah 0,5 (1/2).
• Jumlah kepala menunjukkan jumlah sebenarnya dari lead yang diperoleh.
• Selisih antara jumlah kepala yang sebenarnya dan jumlah kepala yang diharapkan akan meningkat seiring dengan meningkatnya jumlah lemparan.

Jadi di sini, hasilnya tergantung pada berapa kali percobaan diulang. Ini adalah kelemahan utama dari statistik yang sering.

Kelemahan lain yang terkait dengan desain dan teknik interpretasinya menjadi jelas pada abad ke-20 ketika penerapan statistik yang sering pada model numerik mencapai puncaknya.

Keterbatasan Statistik yang Sering

Tiga kelemahan utama dari statistik umum tercantum di bawah ini:

1. Nilai p Variabel

Nilai p yang diukur untuk sampel dengan ukuran tetap dalam percobaan dengan titik akhir yang ditentukan berubah dengan perubahan titik akhir dan ukuran sampel. Ini menghasilkan dua nilai p untuk satu data yang salah.

2. Interval Keyakinan yang Tidak Konsisten

CI (Interval Keyakinan) semata-mata tergantung pada ukuran sampel. Itu membuat potensi berhenti tidak relevan.

3. Nilai Estimasi CI

Interval kepercayaan bukanlah distribusi probabilitas, dan nilainya untuk parameter hanyalah perkiraan dan bukan nilai aktual.

Ketiga alasan di atas melahirkan pendekatan Bayesian yang menerapkan probabilitas pada masalah statistik.

Kelahiran Statistik Bayesian

Pendeta Thomas Bayes pertama kali mengusulkan pendekatan Bayesian untuk statistik dalam esainya yang ditulis pada tahun 1763. Pendekatan ini diterbitkan oleh Richard Price sebagai strategi dalam probabilitas terbalik untuk meramalkan peristiwa masa depan berdasarkan masa lalu.

Pendekatan ini didasarkan pada teorema Bayes yang dijelaskan di bawah ini:

Teorema Bayes

Aksioma probabilitas Renyi menguji probabilitas bersyarat, di mana kemungkinan kejadian A dan kejadian B terjadi bergantung atau bersyarat. Probabilitas kondisional dasar dapat ditulis sebagai:

Peluang terjadinya Kejadian B bergantung pada Kejadian A.

Persamaan di atas adalah dasar dari aturan Bayes, ekspresi matematis dari teorema Bayes yang menyatakan:

Di sini, menunjukkan persimpangan.

Aturan Bayes dapat ditulis sebagai:

Aturan Bayes adalah dasar dari statistik Bayesian, di mana informasi yang tersedia pada parameter tertentu dalam model statistik dibandingkan dan diperbarui dengan data yang dikumpulkan.

Latar belakang pengetahuan direpresentasikan sebagai sebaran sebelumnya, yang kemudian dibandingkan dan dipelajari dengan data yang diamati atau dikumpulkan sebagai fungsi kemungkinan untuk mengetahui distribusi posterior.

Distribusi posterior ini digunakan untuk membuat prediksi tentang peristiwa masa depan.

Penerapan pendekatan Bayesian bergantung pada parameter berikut:

1. Mendefinisikan model prior dan data
2. Membuat kesimpulan yang relevan
3. Meneliti dan merampingkan model

Apa itu Jaringan Neural Bayesian?

Bayesian Neural Networks (BNNs) adalah jaringan yang Anda buat saat Anda memperluas jaringan standar menggunakan metodologi statistik dan mengubah inferensi posterior untuk melacak over-fitting. Karena ini adalah pendekatan Bayesian, ada distribusi probabilitas yang terkait dengan parameter jaringan saraf.

Mereka digunakan untuk memecahkan masalah kompleks di mana tidak ada aliran data gratis yang tersedia. Jaringan saraf Bayesian membantu mengontrol overfitting dalam domain seperti biologi molekuler dan diagnosis medis.

Seseorang dapat mempertimbangkan seluruh distribusi jawaban atas sebuah pertanyaan daripada hanya satu kemungkinan menggunakan jaringan saraf Bayesian. Mereka membantu Anda menentukan pemilihan/perbandingan model dan mengatasi masalah yang melibatkan regularisasi.

Statistik Bayesian menawarkan alat matematika untuk merasionalisasi dan memperbarui pengetahuan subjektif mengenai data baru atau bukti ilmiah. Berbeda dengan pendekatan statistik yang sering, ia berfungsi berdasarkan asumsi bahwa probabilitas bergantung pada frekuensi kejadian yang berulang dalam kondisi yang sama.

Singkatnya, teknik Bayesian adalah perpanjangan dari asumsi dan pendapat individu. Aspek kunci dari model Bayesian yang membuatnya lebih efisien adalah pemahamannya bahwa individu berbeda dalam pendapat mereka berdasarkan jenis informasi yang mereka terima.

Namun, ketika bukti dan data baru muncul, individu memiliki titik konvergensi, inferensi Bayesian . Pembaruan rasional ini adalah fitur khusus dari statistik Bayesian yang membuatnya lebih efektif dalam masalah analitis.

Di sini, probabilitas 0 diterapkan ketika tidak ada harapan untuk suatu peristiwa terjadi, dan probabilitas 1 diterapkan ketika yakin bahwa peristiwa itu akan terjadi. Probabilitas antara 0 dan 1 memberi ruang untuk hasil potensial lainnya.

Aturan Bayes sekarang diterapkan untuk mencapai inferensi Bayesian untuk mendapatkan inferensi yang lebih baik dari model.

Bagaimana Anda menerapkan Aturan Bayes untuk Mendapatkan Inferensi Bayesian?

Pertimbangkan persamaan:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) menunjukkan distribusi sebelumnya,

P(θ|D) menunjukkan keyakinan posterior,

P(D) mewakili bukti,

P(D|θ) menunjukkan kemungkinan.

Tujuan utama dari inferensi Bayesian adalah untuk menawarkan metode yang rasional dan akurat secara matematis untuk memadukan keyakinan dengan bukti untuk mendapatkan keyakinan posterior yang diperbarui. Keyakinan posterior dapat digunakan sebagai keyakinan sebelumnya ketika data baru dihasilkan. Jadi, inferensi Bayesian membantu memperbarui keyakinan secara terus-menerus dengan bantuan aturan Bayes.

Mempertimbangkan contoh lemparan koin yang sama, model Bayesian memperbarui prosedur dari sebelumnya ke keyakinan posterior dengan lemparan koin baru. Metode Bayesian memberikan probabilitas berikut.

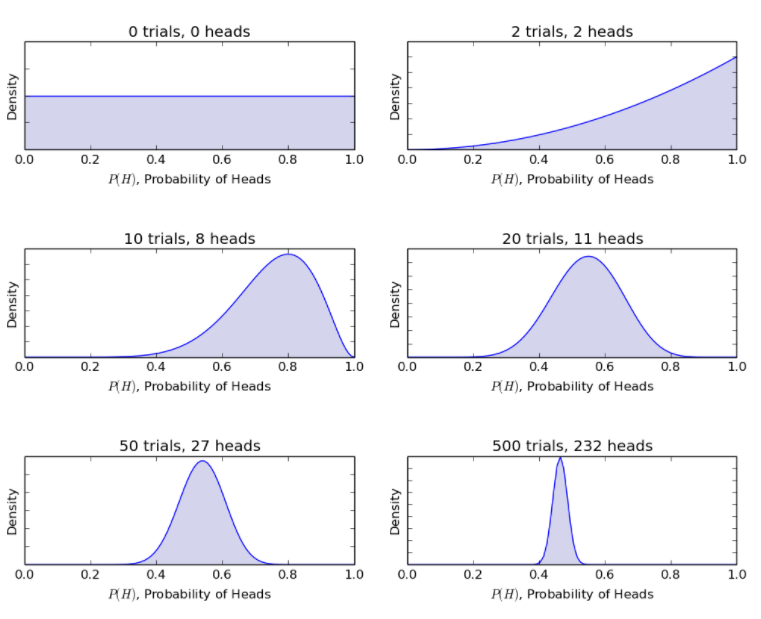
Sumber

Dengan demikian, model Bayesian memungkinkan merasionalisasi skenario yang tidak pasti dengan informasi terbatas ke skenario yang lebih jelas dengan sejumlah besar data.

Perbedaan Penting antara Model Bayesian dan Model Frequentist

Statistik yang sering

Statistik Bayesian

Tujuannya dianggap sebagai perkiraan titik, dan CI

Tujuannya dianggap sebagai distribusi posterior

Prosedurnya dimulai dari pengamatan

Prosesnya dimulai dari distribusi sebelumnya

Setiap kali pengamatan baru dilakukan, pendekatan frequentist menghitung ulang model yang ada.

Setiap kali pengamatan baru dilakukan, distribusi posterior (ideologi/hipotesis) diperbarui

Contoh: Estimasi mean, uji-t, dan ANOVA.

Contoh: Estimasi distribusi posterior rata-rata dan tumpang tindih interval kepadatan tinggi.

Keuntungan dari Statistik Bayesian

• Ini menyediakan cara organik dan sederhana untuk memadukan informasi yang sudah ada sebelumnya dengan kerangka kerja yang solid dengan bukti ilmiah. Informasi masa lalu tentang parameter dapat digunakan untuk membentuk distribusi sebelumnya untuk penyelidikan masa depan. Inferensi mematuhi teorema Bayes.
• Kesimpulan dari model Bayesian logis dan akurat secara matematis dan bukan asumsi kasar. Akurasi tetap konstan terlepas dari ukuran sampel.
• Statistik Bayesian mengikuti prinsip kemungkinan. Ketika dua sampel yang berbeda memiliki fungsi kemungkinan yang sama untuk suatu keyakinan , semua kesimpulan tentang keyakinan tersebut harus serupa. Teknik statistik klasik tidak mengikuti prinsip kemungkinan.
• Solusi dari analisis Bayesian dapat dengan mudah diinterpretasikan.
• Ini menawarkan platform yang kondusif untuk berbagai model seperti model hierarkis dan masalah data yang tidak lengkap. Perhitungan semua model parametrik dapat dilacak secara virtual dengan bantuan teknik numerik lainnya.

Aplikasi Model Bayesian yang Berhasil Sepanjang Sejarah

Metode Bayesian memiliki banyak aplikasi yang berhasil selama Perang Dunia II. Beberapa di antaranya tercantum di bawah ini:

• Seorang ahli statistik Rusia, Andrey Kolmogorov , berhasil menggunakan metode Bayesian untuk meningkatkan efisiensi artileri Rusia.
• Model Bayesian digunakan untuk memecahkan kode kapal U Jerman.
• Seorang matematikawan Amerika kelahiran Prancis, Bernard Koopman, membantu sekutu mengidentifikasi lokasi kapal U Jerman dengan bantuan model Bayesian untuk mencegat transmisi radio.

Jika Anda ingin mempelajari lebih lanjut tentang statistik Bayesian, berikut adalah Sertifikasi Tingkat Lanjut dari Pembelajaran Mesin dan Cloud untuk memahami konsep yang mendasarinya melalui proyek industri kehidupan nyata dan studi kasus. Kursus 12 bulan ditawarkan oleh IIT Madras dan mendukung pembelajaran mandiri.

Hubungi kami untuk detail lebih lanjut.