Contoh Jaringan Bayesian [Dengan Representasi Grafis]

pengantar

Dalam statistik, model Probabilistik digunakan untuk mendefinisikan hubungan antar variabel dan dapat digunakan untuk menghitung probabilitas setiap variabel. Dalam banyak masalah, ada sejumlah besar variabel. Dalam kasus seperti itu, model kondisional sepenuhnya memerlukan sejumlah besar data untuk mencakup setiap kasus dari fungsi probabilitas yang mungkin sulit untuk dihitung secara real-time. Ada beberapa upaya untuk menyederhanakan perhitungan probabilitas bersyarat seperti Naive Bayes tetapi tetap saja, itu tidak terbukti efisien karena secara drastis mengurangi beberapa variabel.

Satu-satunya cara adalah mengembangkan model yang dapat mempertahankan ketergantungan bersyarat antara variabel acak dan kemandirian bersyarat dalam kasus lain. Ini membawa kita pada konsep Bayesian Networks. Bayesian Networks ini membantu kita untuk secara efektif memvisualisasikan model probabilistik untuk setiap domain dan untuk mempelajari hubungan antara variabel acak dalam bentuk grafik yang mudah digunakan.

Pelajari Kursus ML dari Universitas top Dunia. Dapatkan Master, PGP Eksekutif, atau Program Sertifikat Tingkat Lanjut untuk mempercepat karier Anda.

Apa itu Jaringan Bayesian?

Menurut definisi, Bayesian Networks adalah jenis Model Grafis Probabilistik yang menggunakan inferensi Bayesian untuk perhitungan probabilitas. Ini mewakili satu set variabel dan probabilitas bersyarat dengan Directed Acyclic Graph (DAG). Mereka terutama cocok untuk mempertimbangkan suatu peristiwa yang telah terjadi dan memprediksi kemungkinan bahwa salah satu dari beberapa kemungkinan penyebab yang diketahui adalah faktor yang berkontribusi.

Sumber

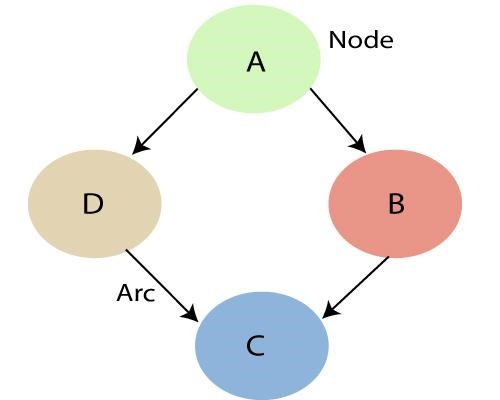
Seperti disebutkan di atas, dengan memanfaatkan hubungan yang ditentukan oleh Jaringan Bayesian, kita dapat memperoleh Distribusi Probabilitas Gabungan (JPF) dengan probabilitas bersyarat. Setiap node dalam grafik mewakili variabel acak dan busur (atau panah terarah) mewakili hubungan antara node. Mereka dapat berupa kontinu atau diskrit di alam.

Dalam diagram di atas A, B, C dan D adalah 4 variabel acak yang diwakili oleh node yang diberikan dalam jaringan grafik. Untuk simpul B, A adalah simpul induknya dan C adalah simpul anaknya. Node C tidak tergantung pada Node A.

Sebelum kita masuk ke implementasi Bayesian Network, ada beberapa dasar probabilitas yang harus dipahami.

Properti Markov Lokal

Jaringan Bayesian memenuhi properti yang dikenal sebagai Properti Markov Lokal. Ini menyatakan bahwa sebuah node independen bersyarat dari non-keturunannya, mengingat orang tuanya. Dalam contoh di atas, P(D|A, B) sama dengan P(D|A) karena D tidak bergantung pada non-keturunannya, B. Sifat ini membantu kita menyederhanakan Distribusi Gabungan. Properti Markov Lokal membawa kita ke konsep Bidang Acak Markov yang merupakan bidang acak di sekitar variabel yang dikatakan mengikuti properti Markov.

Probabilitas Bersyarat

Dalam matematika, Peluang Bersyarat dari peristiwa A adalah peluang bahwa peristiwa A akan terjadi jika peristiwa B lain telah terjadi. Secara sederhana, p(A | B) adalah peluang terjadinya kejadian A, dengan syarat kejadian B terjadi. Akan tetapi, ada dua jenis kemungkinan kejadian antara A dan B. Kemungkinan kejadian tersebut dapat berupa kejadian bergantungan atau kejadian bebas. Tergantung pada jenisnya, ada dua cara berbeda untuk menghitung probabilitas bersyarat.

• Mengingat A dan B adalah kejadian bergantung, probabilitas bersyarat dihitung sebagai P (A| B) = P (A dan B) / P (B)
• Jika A dan B adalah kejadian bebas, maka ekspresi untuk peluang bersyarat diberikan oleh, P(A| B) = P (A)

Distribusi Probabilitas Gabungan

Sebelum kita masuk ke contoh Bayesian Networks, mari kita pahami konsep Distribusi Peluang Bersama. Perhatikan 3 variabel a1, a2 dan a3. Menurut definisi, probabilitas dari semua kemungkinan kombinasi yang berbeda dari a1, a2, dan a3 disebut Distribusi Probabilitas Gabungan.

Jika P[a1,a2, a3,….., an] adalah JPD dari variabel-variabel berikut dari a1 sampai dengan an, maka ada beberapa cara untuk menghitung Distribusi Peluang Bersama sebagai kombinasi dari berbagai istilah seperti,

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., an] * P[a2, a3,….., an]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., an]….P[an-1|an] * P[an]

Generalisasi persamaan di atas, kita dapat menulis Distribusi Peluang Bersama sebagai,

P(X i |X i-1 ,………, X n ) = P(X i |Orang tua(X i ))

Contoh Jaringan Bayesian

Sekarang mari kita memahami mekanisme Bayesian Networks dan kelebihannya dengan bantuan contoh sederhana. Dalam contoh ini, mari kita bayangkan bahwa kita diberi tugas untuk memodelkan nilai siswa ( m ) untuk ujian yang baru saja diberikannya. Dari Grafik Jaringan Bayesian yang diberikan di bawah ini, kita melihat bahwa tanda bergantung pada dua variabel lainnya. Mereka,

• Tingkat Ujian ( e ) – Variabel diskrit ini menunjukkan kesulitan ujian dan memiliki dua nilai (0 untuk mudah dan 1 untuk sulit)
• IQ Level ( i ) – Ini mewakili tingkat Intelligence Quotient siswa dan juga bersifat diskrit yang memiliki dua nilai (0 untuk rendah dan 1 untuk tinggi)

Selain itu, tingkat IQ siswa juga membawa kita ke variabel lain, yaitu Skor Bakat siswa ( s ). Sekarang, dengan nilai yang diperoleh siswa, dia bisa masuk ke universitas tertentu. Distribusi probabilitas untuk diterima ( a ) ke universitas juga diberikan di bawah ini.

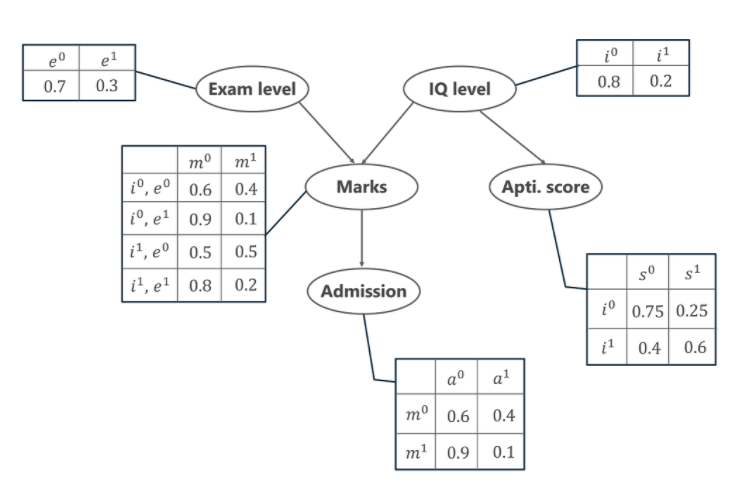
Pada grafik di atas, kita melihat beberapa tabel yang mewakili nilai distribusi probabilitas dari 5 variabel yang diberikan. Tabel ini disebut Tabel Probabilitas Bersyarat atau CPT. Ada beberapa properti dari CPT yang diberikan di bawah ini -

• Jumlah nilai CPT di setiap baris harus sama dengan 1 karena semua kemungkinan kasus untuk variabel tertentu adalah lengkap (mewakili semua kemungkinan).
• Jika suatu variabel yang bersifat Boolean memiliki k parent Boolean, maka dalam CPT memiliki nilai probabilitas 2K.

Kembali ke masalah kita, pertama-tama mari kita daftar semua kemungkinan peristiwa yang terjadi pada tabel yang diberikan di atas.

1. Tingkat Ujian (e)
2. Tingkat IQ (i)
3. Skor Bakat
4. Tanda (m)
5. Penerimaan (a)

Kelima variabel tersebut direpresentasikan dalam bentuk Directed Acyclic Graph (DAG) dalam format Bayesian Network dengan tabel Conditional Probability-nya. Sekarang, untuk menghitung Distribusi Probabilitas Gabungan dari 5 variabel, rumusnya diberikan oleh,

P[a, m, i, e, s]= P(a | m) . P(m | saya, e) . P(i) . Pe) . P(s | saya)

Dari rumus di atas,

• P(a | m) menunjukkan probabilitas bersyarat dari siswa yang diterima berdasarkan nilai yang telah dia cetak dalam ujian.
• P(m | i, e) mewakili nilai yang akan diperoleh siswa berdasarkan tingkat IQ dan tingkat kesulitan Ujiannya.
• P(i) dan P(e) mewakili probabilitas Tingkat IQ dan Tingkat Ujian.
• P(s | i) adalah probabilitas bersyarat dari Skor Bakat siswa, berdasarkan Tingkat IQ-nya.

Dengan probabilitas berikut dihitung, kita dapat menemukan Distribusi Probabilitas Gabungan dari seluruh Jaringan Bayesian.

Perhitungan Distribusi Probabilitas Gabungan

Sekarang mari kita hitung JPD untuk dua kasus.

Kasus 1: Hitung probabilitas bahwa meskipun tingkat ujiannya sulit, siswa yang memiliki tingkat IQ rendah dan Skor Bakat yang rendah, berhasil lulus ujian dan mendapatkan izin masuk ke universitas.

Dari rumusan masalah kata di atas, Distribusi Probabilitas Gabungan dapat ditulis seperti di bawah ini,

P[a=1, m=1, i=0, e=1, s=0]

Dari tabel Probabilitas Bersyarat di atas, nilai untuk kondisi yang diberikan diumpankan ke rumus dan dihitung seperti di bawah ini.

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) . P(m=1 | i=0, e=1) . P(i=0) . P(e=1) . P(s=0 | i=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0,0018

Kasus 2: Dalam kasus lain, hitung probabilitas bahwa siswa tersebut memiliki tingkat IQ dan Skor Bakat Tinggi, ujiannya mudah tetapi gagal lulus dan tidak menjamin masuk ke universitas.

Rumus untuk JPD diberikan oleh

P[a=0, m=0, i=1, e=0, s=1]

Dengan demikian,

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) . P(m=0 | i=1, e=0) . P(i=1) . P(e=0) . P(s=1 | i=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0,0252

Oleh karena itu, dengan cara ini, kita dapat menggunakan Jaringan Bayesian dan tabel Probabilitas untuk menghitung probabilitas berbagai kemungkinan kejadian yang terjadi.

Baca Juga: Ide & Topik Proyek Pembelajaran Mesin

Kesimpulan

Ada banyak sekali aplikasi untuk Bayesian Networks di Spam Filtering, Semantic Search, Information Retrieval, dan banyak lagi. Misalnya, dengan gejala yang diberikan, kita dapat memprediksi kemungkinan terjadinya penyakit dengan beberapa faktor lain yang berkontribusi terhadap penyakit tersebut. Dengan demikian, konsep Jaringan Bayesian diperkenalkan dalam artikel ini bersama dengan implementasinya dengan contoh kehidupan nyata.

Jika Anda ingin menguasai pembelajaran Mesin dan AI, tingkatkan karier Anda dengan Kursus Lanjutan tentang Pembelajaran Mesin dan AI dengan IIIT-B & Liverpool John Moores University.