Teorema Bayes Dijelaskan Dengan Contoh – Panduan Lengkap

pengantar

Apa itu Teorema Bayes?

Teorema Bayes digunakan untuk perhitungan probabilitas bersyarat di mana intuisi sering gagal. Meskipun banyak digunakan dalam probabilitas, teorema ini juga diterapkan di bidang pembelajaran mesin. Penggunaannya dalam pembelajaran mesin mencakup pemasangan model ke set data pelatihan dan mengembangkan model klasifikasi.

Apa itu probabilitas bersyarat?

Probabilitas bersyarat biasanya didefinisikan sebagai probabilitas satu peristiwa mengingat terjadinya peristiwa lain.

• Jika A dan B adalah dua kejadian, maka peluang bersyarat me ditetapkan sebagai P(A diberikan B) atau P(A|B).
• Probabilitas bersyarat dapat dihitung dari probabilitas gabungan (A | B) = P(A, B) / P(B)

• Probabilitas bersyarat tidak simetris; Misalnya P(A | B) != P(B | A)

Cara lain untuk menghitung probabilitas bersyarat termasuk menggunakan probabilitas bersyarat lainnya, yaitu

P(A|B) = P(B|A) * P(A) / P(B)

Terbalik juga digunakan

P(B|A) = P(A|B) * P(B) / P(A)

Cara perhitungan ini berguna ketika sulit untuk menghitung probabilitas gabungan. Lain, ketika probabilitas bersyarat terbalik tersedia, perhitungan melalui ini menjadi mudah.

Perhitungan alternatif probabilitas bersyarat ini disebut sebagai Aturan Bayes atau Teorema Bayes. Itu dinamai di bawah orang yang pertama kali menggambarkannya, "Pendeta Thomas Bayes".

Rumus teorema Bayes

Teorema Bayes adalah cara menghitung probabilitas bersyarat ketika probabilitas bersama tidak tersedia. Terkadang penyebutnya tidak bisa langsung diakses. Dalam kasus seperti itu, cara penghitungan alternatif adalah sebagai berikut:

P(B) = P(B|A) * P(A) + P(B|bukan A) * P(bukan A)

Ini adalah rumusan teorema Bayes yang menunjukkan perhitungan alternatif P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|bukan A) * P(bukan A)

Rumus di atas dapat dijelaskan dengan tanda kurung di sekitar penyebut

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|bukan A) * P(bukan A))

Juga, jika kita memiliki P(A), maka P(bukan A) dapat dihitung sebagai

P(bukan A) = 1 – P(A)

Demikian pula, jika kita memiliki P(bukan B|bukan A), maka P(B|bukan A) dapat dihitung sebagai:

P(B|bukan A) = 1 – P(bukan B|bukan A)

Teorema Bayes dari Peluang Bersyarat

Teorema Bayes terdiri dari beberapa istilah yang namanya diberikan berdasarkan konteks penerapannya dalam persamaan.

Probabilitas posterior mengacu pada hasil P(A|B), dan probabilitas sebelumnya mengacu pada P(A).

• P(A|B): Probabilitas posterior.
• P(A): Probabilitas sebelumnya.

Demikian pula, P(B|A) dan P(B) disebut sebagai kemungkinan dan bukti.

• P(B|A): Kemungkinan.
• P(B): Bukti.

Oleh karena itu, teorema Bayes tentang peluang bersyarat dapat dinyatakan kembali sebagai:

Posterior = Kemungkinan * Sebelumnya / Bukti

Jika kita harus menghitung peluang terjadinya kebakaran karena adanya asap, maka persamaan berikut akan digunakan:

P(Api|Asap) = P(Asap|Api) * P(Api) / P(Asap)

Dimana, P(Fire) adalah Prior, P(Smoke|Fire) adalah Kemungkinan, dan P(Smoke) adalah buktinya.

Ilustrasi Teorema Bayes

Contoh teorema Bayes dijelaskan untuk menggambarkan penggunaan teorema Bayes dalam suatu masalah.

Masalah

Ada tiga kotak berlabel A, B, dan C. Rincian kotak adalah:

• Kotak A berisi 2 bola merah dan 3 bola hitam
• Kotak B berisi 3 bola merah dan 1 bola hitam
• Dan kotak C berisi 1 bola merah dan 4 bola hitam

Ketiga kotak yang identik memiliki peluang yang sama untuk terambil. Jadi, berapa peluang terambilnya bola merah dari kotak A?

Larutan

Misalkan E menyatakan kejadian terambilnya bola merah dan A, B, dan C menyatakan bahwa bola tersebut diambil dari kotaknya masing-masing. Oleh karena itu probabilitas bersyarat adalah P(A|E) yang perlu dihitung.

Probabilitas yang ada P(A) = P(B) = P (C) = 1 / 3, karena semua kotak memiliki probabilitas yang sama untuk terambil.

P(E|A) = Jumlah bola merah di kotak A / Jumlah bola di kotak A = 2 / 5

Demikian pula, P(E|B) = 3/4 dan P(E|C) = 1 / 5

Maka bukti P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Oleh karena itu, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Contoh Teorema Bayes

Teorema Bayes memberikan probabilitas "peristiwa" dengan informasi yang diberikan pada "tes".

• Ada perbedaan antara "peristiwa" dan "tes". Misalnya ada tes penyakit hati, yang berbeda dengan benar-benar menderita penyakit hati, yaitu suatu peristiwa.
• Peristiwa langka mungkin memiliki tingkat positif palsu yang lebih tinggi.

Contoh 1

Berapa probabilitas seorang pasien menderita penyakit hati jika mereka pecandu alkohol?

Di sini, "menjadi pecandu alkohol" adalah "tes" (jenis tes lakmus) untuk penyakit hati.

• A adalah kejadian yaitu “pasien menderita penyakit liver””.

Berdasarkan catatan klinik sebelumnya, disebutkan bahwa 10% pasien yang masuk klinik menderita penyakit liver.

Oleh karena itu, P(A)=0,10

• B adalah tes lakmus bahwa "Pasien adalah seorang alkoholik".

Catatan sebelumnya dari klinik menunjukkan bahwa 5% dari pasien yang memasuki klinik adalah pecandu alkohol.

Oleh karena itu, P(B)=0,05

• Juga, 7% dari pasien yang didiagnosis dengan penyakit hati, adalah pecandu alkohol. Ini mendefinisikan B|A: probabilitas seorang pasien menjadi pecandu alkohol, mengingat bahwa mereka memiliki penyakit hati adalah 7%.

Sebagai, per rumus teorema Bayes ,

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Oleh karena itu, untuk pasien yang alkoholik, kemungkinan menderita penyakit hati adalah 0,14 (14%).

Contoh2

• Kebakaran berbahaya jarang terjadi (1%)
• Tapi asap cukup umum (10%) karena barbekyu,
• Dan 90% kebakaran berbahaya menghasilkan asap

Berapa probabilitas Kebakaran berbahaya ketika ada Asap?

Perhitungan

P(Api|Asap) =P(Api) P(Asap|Api)/P(Asap)

= 1% x 90%/10%

= 9%

Contoh 3

Berapa peluang hujan pada siang hari? Dimana, Rain berarti hujan di siang hari, dan Cloud berarti pagi yang mendung.

Peluang Hujan yang diberikan Cloud ditulis P(Rain|Cloud)

P(Hujan|Awan) = P(Hujan) P(Awan|Hujan)/P(Awan)

P(Hujan) adalah Peluang Hujan = 10%

P(Cloud|Rain) adalah Probabilitas Awan, mengingat terjadi Hujan = 50%

P(Cloud) adalah Probabilitas Cloud = 40%

P(Hujan|Awan) = 0,1 x 0,5/0,4 = 0,125

Oleh karena itu, peluang hujan 12,5%.

Aplikasi

Beberapa aplikasi teorema Bayes ada di dunia nyata. Beberapa aplikasi utama dari teorema adalah:

1. Pemodelan Hipotesis

Teorema Bayes menemukan aplikasi luas dalam pembelajaran mesin yang diterapkan dan menetapkan hubungan antara data dan model. Pembelajaran mesin terapan menggunakan proses pengujian dan analisis hipotesis yang berbeda pada kumpulan data yang diberikan.

Untuk menggambarkan hubungan antara data dan model, teorema Bayes menyediakan model probabilistik.

P(h|D) = P(D|h) * P(h) / P(D)

Di mana,

P(h|D): Probabilitas posterior dari hipotesis

P(h): Probabilitas hipotesis sebelumnya.

Kenaikan P(D) menurunkan P(h|D). Sebaliknya, jika P(h) dan probabilitas mengamati data yang diberikan hipotesis meningkat, maka probabilitas P(h|D) meningkat.

2. Teorema Bayes untuk Klasifikasi

Metode klasifikasi melibatkan pelabelan data yang diberikan. Ini dapat didefinisikan sebagai perhitungan probabilitas bersyarat dari label kelas yang diberikan sampel data.

P(kelas|data) = (P(data|kelas) * P(kelas)) / P(data)

Di mana P(class|data) adalah probabilitas kelas yang diberikan data yang disediakan.

Perhitungan dapat dilakukan untuk setiap kelas. Kelas yang memiliki probabilitas terbesar dapat ditugaskan ke data input.

Perhitungan probabilitas bersyarat tidak layak di bawah kondisi sejumlah kecil contoh. Oleh karena itu, penerapan langsung teorema Bayes tidak layak. Solusi untuk model klasifikasi terletak pada perhitungan yang disederhanakan.

• Pengklasifikasi Naive Bayes

Teorema Bayes menganggap bahwa variabel input bergantung pada variabel lain yang menyebabkan kompleksitas perhitungan. Oleh karena itu, asumsi tersebut dihilangkan dan setiap variabel input dianggap sebagai variabel independen. Akibatnya model berubah dari model probabilitas bersyarat dependen menjadi independen. Ini pada akhirnya mengurangi kompleksitas.

Penyederhanaan teorema Bayes ini disebut sebagai Naive Bayes. Ini banyak digunakan untuk klasifikasi dan model prediksi.

• Pengklasifikasi Bayes Optimal

Ini adalah jenis model probabilistik yang melibatkan prediksi contoh baru yang diberikan dataset pelatihan. Salah satu contoh Bayes Optimal Classifier adalah “Apa klasifikasi yang paling mungkin dari instance baru yang diberikan data pelatihan?”

Perhitungan probabilitas bersyarat dari sebuah instance baru yang diberikan data pelatihan dapat dilakukan melalui persamaan berikut:

P(vj | D) = jumlah {h dalam H} P(vj | hai) * P(hi | D)

Di mana vj adalah instance baru untuk diklasifikasikan,

H adalah himpunan hipotesis untuk mengklasifikasikan contoh,

hai adalah hipotesis yang diberikan,

P(vj | hi) adalah probabilitas posterior untuk vi yang diberikan hipotesis hi, dan

P(hi | D) adalah probabilitas posterior dari hipotesis hi jika diberikan data D.

3. Penggunaan teorema Bayes dalam Pembelajaran mesin

Aplikasi teorema Bayes yang paling umum dalam pembelajaran mesin adalah pengembangan masalah klasifikasi. Aplikasi lain selain klasifikasi termasuk optimasi dan model kasual.

• Optimasi Bayesian

Itu selalu merupakan tugas yang menantang untuk menemukan input yang menghasilkan biaya minimum atau maksimum dari fungsi tujuan tertentu. Optimasi Bayesian didasarkan pada teorema Bayes dan menyediakan aspek untuk pencarian masalah optimasi global. Metode tersebut meliputi pembangunan model probabilistik (fungsi pengganti), pencarian melalui fungsi akuisisi, dan pemilihan calon sampel untuk mengevaluasi fungsi tujuan yang sebenarnya.

Dalam pembelajaran mesin terapan, optimasi Bayesian digunakan untuk menyetel hyperparameter dari model berperforma baik.

• Jaringan Kepercayaan Bayesian

Hubungan antara variabel dapat didefinisikan melalui penggunaan model probabilistik. Mereka juga digunakan untuk perhitungan probabilitas. Model probabilitas bersyarat penuh mungkin tidak dapat menghitung probabilitas karena volume data yang besar. Naive Bayes telah menyederhanakan pendekatan untuk perhitungan. Namun metode lain ada di mana model dikembangkan berdasarkan ketergantungan bersyarat yang diketahui antara variabel acak dan independensi bersyarat dalam kasus lain. Jaringan Bayesian menampilkan ketergantungan dan kemandirian ini melalui model graf probabilistik dengan tepi berarah. Ketergantungan bersyarat yang diketahui ditampilkan sebagai tepi berarah dan koneksi yang hilang mewakili kemandirian bersyarat dalam model.

4. Pemfilteran Spam Bayesian

Penyaringan spam adalah aplikasi lain dari teorema Bayes. Ada dua acara yang hadir:

• Peristiwa A: Pesannya adalah spam.
• Tes X: Pesan berisi kata-kata tertentu (X)

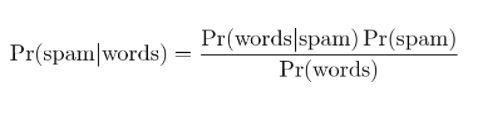
Dengan penerapan teorema Bayes, dapat diprediksi jika pesan tersebut adalah spam yang diberikan “hasil pengujian”. Menganalisis kata-kata dalam sebuah pesan dapat menghitung kemungkinan menjadi pesan spam. Dengan pelatihan filter dengan pesan berulang, ini memperbarui fakta bahwa kemungkinan memiliki kata-kata tertentu dalam pesan akan menjadi spam.

Aplikasi teorema Bayes dengan contoh

Produsen katalis menghasilkan perangkat untuk menguji cacat pada elektrokatalis (EC) tertentu. Produsen katalis mengklaim bahwa pengujian tersebut 97% dapat diandalkan jika EC rusak dan 99% dapat diandalkan jika sempurna. Namun, 4% dari EC tersebut diperkirakan akan rusak saat pengiriman. Aturan Bayes diterapkan untuk memastikan keandalan perangkat yang sebenarnya. Rangkaian acara dasar adalah

A : EC rusak; A': EC sempurna; B: EC diuji cacat; B': EC diuji sempurna.

Kemungkinannya adalah

B/A: EC (diketahui) cacat, dan diuji cacat, P(B/A) = 0,97,

B'/A: EC (diketahui) cacat, tetapi diuji tanpa cacat, P(B'/A)=1-P(B/A)=0,03,

B/A': EC (diketahui) cacat, tetapi diuji cacat, P(B/A') = 1- P(B'/A')=0,01

B'/A: = EC (dikenal sebagai) sempurna, dan diuji tanpa cacat P(B'/A') = 0,99

Probabilitas yang dihitung dengan teorema Bayes adalah:

Probabilitas komputasi menunjukkan bahwa ada kemungkinan besar untuk menolak EC yang sempurna (sekitar 20%) dan kemungkinan yang rendah untuk mengidentifikasi EC yang rusak (sekitar 80%).

Kesimpulan

Salah satu fitur yang paling mencolok dari teorema Bayes adalah bahwa dari beberapa rasio probabilitas, sejumlah besar informasi dapat diperoleh. Dengan cara kemungkinan, probabilitas peristiwa sebelumnya dapat ditransformasikan ke probabilitas posterior. Pendekatan teorema Bayes dapat diterapkan di bidang statistik, epistemologi, dan logika induktif.

Jika Anda tertarik untuk mempelajari lebih lanjut tentang Teorema Bayes, AI, dan pembelajaran mesin, lihat Program PG Eksekutif IIIT-B & upGrad dalam Pembelajaran Mesin & AI yang dirancang untuk profesional yang bekerja dan menawarkan 450+ jam pelatihan ketat, 30+ kasus studi & tugas, status Alumni IIIT-B, 5+ proyek batu penjuru praktis & bantuan pekerjaan dengan perusahaan-perusahaan top.