Qu'est-ce que la pensée bayésienne ? Introduction et théorème

Un théorème statistique donné par le statisticien et philosophe anglais Thomas Bayes dans les années 1700 continue d'être un guide pour les scientifiques et les analystes du monde entier. Aujourd'hui, la pensée bayésienne trouve une application dans la médecine, la science, la technologie et plusieurs autres disciplines et continue d'influencer fortement notre vision du monde et les actions qui en résultent.

L'idée de Bayes de Thomas était étonnamment simple. Selon Bayes, la probabilité qu'une hypothèse soit vraie dépend de deux conditions : dans quelle mesure elle est raisonnable sur la base de ce que nous savons déjà (les connaissances antérieures) et dans quelle mesure elle correspond à de nouvelles preuves. Ainsi, la pensée bayésienne diffère des tests d'hypothèse traditionnels en ce que la première inclut les connaissances antérieures avant de sauter aux conclusions.

Avec l'introduction préliminaire à l'esprit, plongeons un peu plus dans les détails des statistiques bayésiennes.

Statistiques bayésiennes

En termes simples, les statistiques bayésiennes appliquent des probabilités à des problèmes statistiques pour mettre à jour les croyances antérieures à la lumière des preuves de nouvelles données. La probabilité exprime un degré de croyance en un événement spécifique.

Le degré de croyance peut être basé sur une connaissance antérieure de l'événement basée sur des hypothèses personnelles ou sur les résultats d'expériences antérieures. Les statistiques bayésiennes utilisent le théorème de Bayes pour calculer les probabilités. Le théorème de Bayes, à son tour, décrit la probabilité conditionnelle d'un événement sur la base de nouvelles preuves et d'informations antérieures liées à l'événement.

Dans cet esprit, rafraîchissons-nous le concept fondamental de probabilité conditionnelle avant de comprendre en profondeur le théorème de Bayes.

Probabilite conditionnelle

La probabilité conditionnelle peut être définie comme la probabilité d'un événement ou d'un résultat basé sur l'occurrence d'un événement ou d'un résultat précédent. Il est calculé en multipliant la probabilité de l'événement précédent par la probabilité de l'événement suivant ou conditionnel.

Prenons un exemple pour mieux comprendre le concept .

• L'événement A est qu'une famille qui planifie une sortie ira en pique-nique. Il y a 80 % de chances que la famille aille pique-niquer.
• L'événement B est qu'il va pleuvoir le jour où la famille va pique-niquer. Les prévisions météorologiques indiquent qu'il y a 60 % de chances de précipitations le jour du pique-nique.
• Ainsi, la probabilité (P) que la famille parte en pique-nique et qu'il pleuve se calcule comme suit :

P (Pique-nique et pluie) = P (Pluie | Pique-nique) P (Pique-nique) = (0,60) * (0,80) = 0,48

Dans l'exemple ci-dessus, la probabilité conditionnelle examine les deux événements A et B en relation l'un avec l'autre, c'est-à-dire la probabilité que la famille aille au pique-nique et qu'il pleuve également le même jour.

Par conséquent, la probabilité conditionnelle diffère de la probabilité inconditionnelle car cette dernière fait référence à la probabilité d'occurrence d'un événement, qu'un ou plusieurs autres événements se soient produits ou que d'autres conditions soient présentes.

La formule de la probabilité conditionnelle

La formule de probabilité conditionnelle provient de la règle de multiplication de probabilité :

P (A et B) ou P (AUB) = P ( B étant donné A) ou P (B | A) * P (A)

Dans l'équation ci-dessus, P (A et B) est la probabilité conjointe, se référant à la probabilité que deux événements ou plus se produisent simultanément. Il s'écrit aussi P (A,B).

Voici comment déduire l'équation de probabilité conditionnelle de la règle de multiplication :

Étape 1 : Notez la règle de multiplication.

P (A et B) = P (B | A) * P (A)

Étape 2 : Divisez les deux membres de l'équation par P (A).

P (A et B) / P (A) = P (B | A) * P (A) / P (A)

Étape 3 : Annuler P (A) sur le côté droit de l'équation.

P (A et B) / P (A) = P (B | A)

Étape 4 : réécrivez l'équation.

P (A et B) = P (B | A) / P (A)

Ainsi, la formule de probabilité conditionnelle est donnée par :

P (A et B) = P (B | A) / P (A)

Théorème de Bayes

En utilisant le théorème de Bayes, nous pouvons mettre à jour nos croyances et nos convictions sur la base d'éléments de preuve nouveaux et pertinents. Par exemple, si nous essayons de déterminer la probabilité qu'une personne donnée ait un cancer, nous supposons généralement qu'il s'agit du pourcentage de la population atteinte d'un cancer. Cependant, si nous introduisons des preuves supplémentaires, telles que la personne en question est un fumeur régulier, nous pouvons mettre à jour notre perception (et donc la probabilité) puisque la probabilité d'avoir un cancer est plus élevée si un individu est un fumeur. Par conséquent, nous utilisons à la fois nos connaissances antérieures et les preuves supplémentaires pour améliorer nos estimations.

La formule du théorème de Bayes

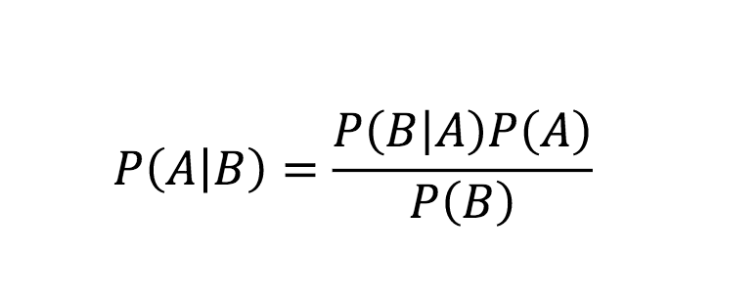
La source

L'équation ci-dessus est la règle de Bayes. Examinons maintenant la dérivation pas à pas de l'équation du théorème de Bayes.

Étape 1 : Considérez deux événements, A et B. A est l'événement dont nous voulons calculer la probabilité et B est la preuve supplémentaire liée à A.

Étape 2 : Notez la relation entre la probabilité conjointe et la probabilité conditionnelle des événements A et B.

P (A,B) = P (A | B) * P(B) = P (B,A) = P (B | A) * P(A)

Étape 3 : Définissez les deux termes de probabilité conditionnelle égaux l'un à l'autre.

P (A | B) * P(B) = P (B | A) * P(A)

Étape 4 : Divisez les deux côtés de l'équation par P (B).

P (A | B) * P(B) / P (B) = P (B | A) * P(A) / P (B)

Étape 5 : Annulez P (B) sur le côté gauche de l'équation.

P (A | B) = P (B | A) * P(A) / P (B)

Ainsi, nous obtenons la formule du théorème de Bayes comme suit :

P (A | B) = P (B | A) * P(A) / P (B)

Comprendre les termes de l'équation du théorème de Bayes

P (A | B) = P (B | A) * P(A) / P (B)

• P (A | B) est appelée la probabilité postérieure ou la probabilité que nous essayons d'estimer. Sur la base de l'exemple précédent, la probabilité a posteriori serait la probabilité que la personne ait un cancer, étant donné que la personne est un fumeur régulier.
• P (B | A) est appelé la vraisemblance , se référant à la probabilité de détecter la preuve supplémentaire, compte tenu de notre hypothèse initiale. Dans l'exemple ci-dessus, la vraisemblance est la probabilité que la personne fume, étant donné qu'elle a un cancer.
• P (A) est la probabilité a priori ou la probabilité de notre hypothèse sans aucune preuve ou information supplémentaire. Dans l'exemple ci-dessus, la probabilité a priori est la probabilité d'avoir un cancer.
• P (B) est la probabilité marginale ou la probabilité totale d'observer la preuve. Dans le contexte de l'exemple ci-dessus, la probabilité marginale est la probabilité d'être fumeur.

Un exemple simple pour comprendre le théorème de Bayes

En utilisant des nombres hypothétiques dans l'exemple précédent, nous verrons l'effet de l'application du théorème de Bayes.

Supposons que la probabilité d'avoir un cancer est de 0,06, c'est-à-dire que 6 % des personnes ont un cancer. Maintenant, disons que la probabilité d'être fumeur est de 0,20 ou 20 % des personnes sont des fumeurs, et 30 % des personnes atteintes de cancer sont des fumeurs. Donc, P (Fumeur | Cancer) = 0,30.

Initialement, la probabilité d'avoir un cancer est simplement de 0,06 (avant). Mais en utilisant les nouvelles preuves, nous pouvons calculer P (Cancer | Fumeur) = P ((Fumeur | Cancer) * P (Cancer)) / P (Fumeur) = (0,30*0,06) / (0,20) = 0,09.

Apprenez des cours de science des données en ligne dans les meilleures universités du monde. Gagnez des programmes Executive PG, des programmes de certificat avancés ou des programmes de maîtrise pour accélérer votre carrière.

Aller de l'avant : maîtriser les concepts de statistiques pour une carrière en science des données ou en apprentissage automatique

La plate-forme d'apprentissage EdTech supérieure d'upGrad a touché plus de 500 000 professionnels dans le monde entier avec sa pléthore de cours et d'expériences d'apprentissage immersives. Avec une base de plus de 40 000 apprenants répartis dans plus de 85 pays, les cours pertinents pour l'industrie d'upGrad sont garantis pour faire progresser votre carrière dans le domaine de votre choix.

Master of Science in Data Science est un cours de 18 mois conférant des compétences clés en statistiques, analyse prédictive, apprentissage automatique, analyse de données volumineuses, visualisation de données, etc.

Faits saillants du programme :

• Master de l'Université John Moores de Liverpool et Executive PGP de l'IIIT Bangalore
• Plus de 500 heures de contenu, plus de 60 études de cas et projets, plus de 20 sessions en direct, plus de 14 langages et outils de programmation
• Mise en réseau de l'industrie, séances de résolution de doutes et soutien à l'apprentissage

Le programme de certificat avancé en apprentissage automatique et en apprentissage en profondeur est un cours rigoureux de 6 mois avec des opportunités de réseautage entre pairs, des projets pratiques, un mentorat de l'industrie et une assistance professionnelle à 360 degrés.

Faits saillants du programme :

• Reconnaissance prestigieuse de l'IIIT Bangalore
• Plus de 240 heures de contenu, plus de 5 études de cas et projets, plus de 24 sessions en direct, couverture de 12 langages de programmation, outils et bibliothèques
• Séances de coaching de groupe 1:8 et séances de mentorat 1:1 avec des experts de l'industrie

Conclusion

La pensée bayésienne sous-tend plusieurs domaines de la pensée, de la recherche et de la croyance humaines, même si la plupart d'entre nous n'en sommes pas conscients. Du dépistage du cancer au réchauffement climatique en passant par la politique monétaire, l'évaluation des risques et l'assurance , la pensée bayésienne est fondamentale. Même le célèbre mathématicien britannique Alan Turing aurait utilisé l'approche bayésienne pour déchiffrer le code Enigma allemand pendant la Seconde Guerre mondiale.

Inscrivez-vous à upGrad et approfondissez vos connaissances sur les concepts statistiques clés et plus encore !