Premiers pas avec la régression binomiale négative : guide étape par étape

La technique de la Régression Binomiale Négative est utilisée pour effectuer la modélisation des variables de comptage. La méthode est presque similaire à la méthode de régression multiple. Cependant, il y a la différence que dans le cas de la régression binomiale négative, la variable dépendante, c'est-à-dire Y, suit la distribution binomiale négative. Par conséquent, les valeurs de la variable peuvent être des entiers non négatifs tels que 0, 1, 2.

La méthode est également une extension de la régression de Poisson qui fait une relaxation en supposant que la moyenne est égale à la variance. L'un des modèles traditionnels de régression binomiale, défini comme "NB2", est basé sur la distribution mixte de Poisson-gamma.

La méthode de la régression de Poisson est généralisée par l'ajout d'une variable de bruit gamma. Cette variable a une valeur de moyenne un et également un paramètre d'échelle qui est "v".

Voici quelques exemples de la régression binomiale négative :

• Les administrateurs de l'école ont mené une étude pour étudier le comportement d'assiduité des élèves du secondaire de deux écoles. Les facteurs qui pourraient influencer le comportement d'assiduité pourraient inclure les jours où les juniors étaient absents de l'école. Aussi, le programme auquel ils étaient inscrits.
• Un chercheur d'une étude liée à la santé a mené une étude sur le nombre de personnes âgées ayant visité un hôpital au cours des 12 derniers mois. L'étude était basée sur les caractéristiques de l'individu et les plans de santé que les personnes âgées ont achetés.

Exemple de régression binomiale négative

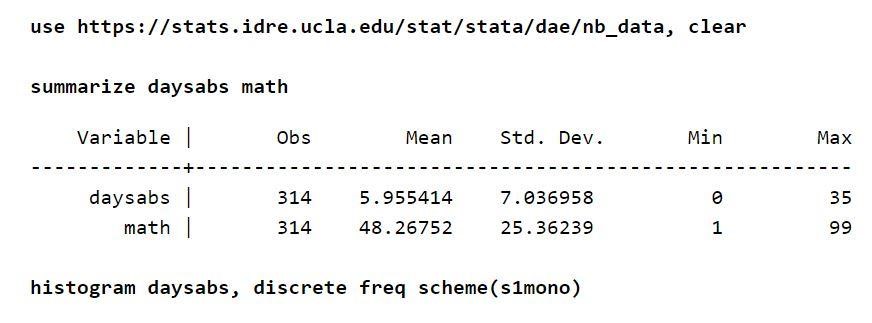
Supposons qu'il existe une feuille de présence d'environ 314 élèves du secondaire. Les données sont extraites de deux écoles urbaines et stockées dans un fichier nommé nb_data.dta. La variable de réponse intéressante dans cet exemple est les jours d'absence qui sont des "daysabs". Une variable, "maths", est présente, qui définit le score en mathématiques de chaque élève. Il y a une autre variable qui est « prog ». Cette variable indique le programme auquel les étudiants sont inscrits.

La source

Chacune des variables a environ 314 observations. Par conséquent, les distributions entre les variables sont également raisonnables. De plus, compte tenu de la variable de résultat, la moyenne inconditionnelle est inférieure à la variance.

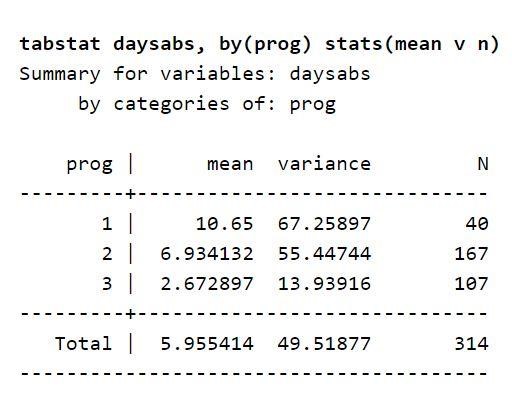
Maintenant, concentrez-vous sur la description de la variable considérée dans l'ensemble de données. Un tableau présente le nombre moyen de jours d'absence d'un élève dans chaque type de programme. Cela suggère que le programme de type variable peut prédire les jours d'absence de l'élève à l'école. Vous pouvez également l'utiliser pour prédire la variable de résultat. En effet, la valeur moyenne de la variable de résultat varie selon la variable prog. De plus, les valeurs des variances sont supérieures à celles de chaque niveau de la variable prog. Ces valeurs sont appelées variances et moyennes. Les différences existantes suggèrent qu'il y a présence de sur-dispersion, et il sera donc approprié d'utiliser un modèle binomial négatif.

La source

Un chercheur peut envisager plusieurs méthodes d'analyse pour ce type d'étude. Ces méthodes sont décrites ci-dessous. Voici quelques-unes des méthodes d'analyse que l'utilisateur peut utiliser pour analyser le modèle de régression :

1. Régression binomiale négative

La méthode de régression binomiale négative doit être utilisée lorsqu'il y a des données surdispersées. Cela signifie que la valeur de la variance conditionnelle est supérieure ou supérieure à la valeur de la moyenne conditionnelle. La méthode est considérée comme généralisée à partir de la méthode de régression de Poisson. En effet, les deux méthodes ont la même structure de la moyenne. Mais, il existe un paramètre supplémentaire dans la régression binomiale négative utilisée pour modéliser la surdispersion. Les intervalles de confiance sont considérés comme plus étroits que la régression passionnelle lorsque la distribution conditionnelle est trop dispersée par rapport à la variable de résultat.

2. Régression de Poisson

La méthode de régression de Poisson est utilisée dans la modélisation des données de comptage. De nombreuses extensions peuvent être utilisées pour modéliser les variables de comptage dans la régression de Poisson.

3. Régression MCO

Les résultats des variables de comptage sont parfois transformés en log, puis analysés par la méthode de régression OLS. Cependant, il y a parfois des problèmes liés à la méthode de régression OLS. Ces problèmes peuvent être la perte de données due à la génération de toute valeur indéfinie en tenant compte du journal de la valeur zéro. En outre, il peut être généré en raison du manque de modélisation des données dispersées.

4. Modèles sans gonflage

Ces types de modèles tentent de tenir compte de tous les zéros en excès dans le modèle.

Analyse utilisant la régression binomiale négative

La commande "nbreg" est utilisée pour estimer le modèle de régression binomiale négative. Il y a un "i" avant la variable "prog". La présence de « i » indique que la variable est de type facteur, c'est-à-dire variable catégorielle. Ceux-ci devraient être inclus comme variables indicatrices dans le modèle.

• La sortie du modèle commence par un journal d'itération. Elle commence par l'ajustement du modèle de Poisson, suivi d'un modèle nul, puis du modèle du binôme négatif. La méthode utilise l'estimation du maximum de vraisemblance et continue d'itérer jusqu'à ce qu'il y ait un changement dans la valeur du log final. La vraisemblance du log est utilisée pour la comparaison des modèles.
• Les informations suivantes se trouvent dans le fichier d'en-tête.
• Il y a les informations des coefficients de la régression binomiale négative juste en dessous de l'en-tête. Les coefficients sont générés pour chaque variable avec les erreurs telles que les valeurs p, les scores z. Il existe également un intervalle de confiance de 95% pour tous les coefficients. Le coefficient de la variable « maths » est de -0,006, ce qui indique qu'elle est statistiquement significative. Le résultat signifie que s'il y a une augmentation d'une unité sur la variable "maths", le nombre de logs attendu pour le nombre de jours d'absence diminue d'une valeur de 0,006. De plus, la valeur du 2. prog, la variable indicatrice, est la différence attendue dans le nombre de log entre les deux groupes (groupe 2 et groupe de référence).
• L'estimation des paramètres pour la surdispersion logarithmique transférée est effectuée puis affichée avec la valeur non transformée. Dans le modèle de Poisson, la valeur est zéro.
• Il y a une information de probabilité de test de rapport sous le tableau des coefficients. Le modèle peut être mieux compris grâce à l'utilisation des commandes "marges".

Processus d'analyse de régression binomiale négative en Python

Les packages requis pour effectuer le processus de régression doivent être importés depuis Python. Ces forfaits sont listés ci-dessous :

• importer statsmodels.api en tant que sm
• importer matplotlib.pyplot en tant que plt
• importer numpy en tant que np
• de patsy importer des matrices
• importer des pandas en tant que pd

Considérations relatives à la régression binomiale négative

Il y a quelques éléments à prendre en compte lors de l'application de la méthode d'analyse de régression binomiale négative. Ceux-ci inclus:

• S'il y a présence de petits échantillons, la méthode de régression binomiale négative n'est pas recommandée.
• Parfois, il y a des zéros en excès qui pourraient être une cause de la surdispersion. Ces zéros peuvent être générés en raison du processus d'ajout de génération de données. Si un tel type de cas se produit, il est recommandé d'utiliser la méthode du modèle à gonflage zéro.
• Si le processus de génération de données ne prend pas en compte les zéros, alors dans de tels cas, il est recommandé d'utiliser la méthode du modèle zéro tronqué.
• Une variable d'exposition est associée aux données de comptage. La variable indique les moments où il y a une chance que l'événement se produise. Cette variable doit être incorporée dans le modèle de régression binomiale négative. Cela se fait via l'option de exp().
• La variable de résultat ne peut pas être une valeur négative dans le modèle de l'analyse de régression binomiale négative. De plus, la variable d'exposition ne peut pas avoir la valeur 0.
• La commande « glm » peut également être utilisée pour exécuter une méthode d'analyse de régression binomiale négative. Cela peut se faire via le lien du journal et aussi la famille des binômes.
• La commande « glm » est nécessaire pour obtenir les résidus. Il s'agit de vérifier s'il existe d'autres hypothèses dans le modèle de régression binomiale négative.
• Il y a l'existence des différentes mesures du pseudo-R-carré. Cependant, chaque mesure fournit des informations similaires aux informations fournies par le R au carré dans la régression des MCO.

Conclusion

L'article a abordé le sujet de la régression binomiale négative . Nous avons vu qu'elle est presque similaire à la méthode des régressions multiples et qu'elle est une forme généralisée de la distribution de Poisson. Il existe plusieurs applications de la méthode. La technique peut également être appliquée via le langage de programmation python ou en R.

Plusieurs études de cas sont également présentes qui montrent son application dans des études telles que le vieillissement. En outre, les modèles classiques de régressions pouvant être utilisés sur les données de comptage sont la régression de Poisson, la régression binomiale négative et la régression géométrique. Ces méthodes appartenaient à la famille des modèles linéaires et étaient incluses dans presque tous les packages statistiques tels que le système R.

Si vous souhaitez exceller en machine learning et explorer le domaine des données, vous pouvez consulter le cours Executive PG Program in Machine Learning & AI proposé par upGrad. Donc, si vous êtes un professionnel en activité qui rêve d'être un expert en apprentissage automatique, venez acquérir l'expérience de vous former auprès d'experts. Plus de détails peuvent être obtenus via notre site Web. Pour toute question, notre équipe peut vous aider rapidement.

Améliorez votre carrière dans l'apprentissage automatique et l'intelligence artificielle

Postulez maintenant pour la certification exécutive en Ai-ml de l'IIITB