Apprenez l'algorithme naïf de Bayes pour l'apprentissage automatique [avec exemples]
Publié: 2021-02-25Table des matières
introduction
En mathématiques et en programmation, certaines des solutions les plus simples sont généralement les plus puissantes. L'algorithme naïf de Bayes est un exemple classique de cette affirmation. Même avec les progrès et le développement forts et rapides dans le domaine de l'apprentissage automatique, cet algorithme naïf de Bayes reste l'un des algorithmes les plus utilisés et les plus efficaces. L'algorithme naïf de Bayes trouve ses applications dans une variété de problèmes, notamment les tâches de classification et les problèmes de traitement du langage naturel (TAL).
L'hypothèse mathématique du théorème de Bayes sert de concept fondamental derrière cet algorithme naïf de Bayes. Dans cet article, nous allons passer en revue les bases du théorème de Bayes, l'algorithme Naive Bayes ainsi que son implémentation en Python avec un exemple de problème en temps réel. Parallèlement à cela, nous examinerons également certains avantages et inconvénients de l'algorithme Naive Bayes par rapport à ses concurrents.
Bases de la probabilité
Avant de nous aventurer à comprendre le théorème de Bayes et l'algorithme naïf de Bayes, rafraîchissons nos connaissances existantes sur les principes fondamentaux de la probabilité.
Comme nous le savons tous par définition, étant donné un événement A, la probabilité que cet événement se produise est donnée par P(A). En probabilité, deux événements A et B sont qualifiés d'événements indépendants si l'occurrence de l'événement A ne modifie pas la probabilité d'occurrence de l'événement B et vice versa. D'autre part, si l'occurrence de l'un modifie la probabilité de l'autre, alors ils sont appelés événements dépendants.
Laissez-nous vous présenter un nouveau terme appelé probabilité conditionnelle . En mathématiques, la probabilité conditionnelle pour deux événements A et B donnés par P (A | B) est définie comme la probabilité d'occurrence de l'événement A étant donné que l'événement B s'est déjà produit. Selon la relation entre les deux événements A et B quant à savoir s'ils sont dépendants ou indépendants, la probabilité conditionnelle est calculée de deux manières.
- La probabilité conditionnelle de deux événements dépendants A et B est donnée par P (A | B) = P (A et B) / P (B)
- L'expression de la probabilité conditionnelle de deux événements indépendants A et B est donnée par, P (A | B) = P (A)
Connaissant les mathématiques derrière les probabilités et les probabilités conditionnelles, passons maintenant au théorème de Bayes.

Théorème de Bayes
En statistique et en théorie des probabilités, le théorème de Bayes, également connu sous le nom de règle de Bayes, est utilisé pour déterminer la probabilité conditionnelle des événements. En d'autres termes, le théorème de Bayes décrit la probabilité d'un événement sur la base d'une connaissance préalable des conditions qui pourraient être pertinentes pour l'événement.
Pour le comprendre de manière plus simple, considérons que nous devons savoir que la probabilité que le prix d'une maison soit très élevée. Si nous connaissons les autres paramètres tels que la présence d'écoles, de cabinets médicaux et d'hôpitaux à proximité, nous pouvons alors en faire une évaluation plus précise. C'est exactement ce que fait le théorème de Bayes.
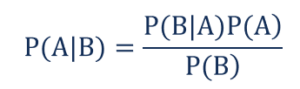
Tel que,
- P(A|B) - la probabilité conditionnelle que l'événement A se produise, étant donné que l'événement B s'est produit, également connu sous le nom de probabilité postérieure .
- P(B|A) - la probabilité conditionnelle que l'événement B se produise, étant donné que l'événement A s'est produit, également connu sous le nom de probabilité de probabilité .
- P(A) – la probabilité que l'événement A se produise également connu sous le nom de probabilité a priori.
- P(B) – la probabilité que l'événement B se produise, également connue sous le nom de probabilité marginale.
Supposons que nous ayons un simple problème d'apprentissage automatique avec 'n' variables indépendantes et que la variable dépendante qui est la sortie est une valeur booléenne (vrai ou faux). Supposons que les attributs indépendants soient de nature catégorielle, considérons 2 catégories pour cet exemple. Par conséquent, avec ces données, nous devons calculer la valeur de la probabilité de vraisemblance, P(B|A).
Par conséquent, en observant ce qui précède, nous constatons que nous devons calculer 2*(2^ n -1 ) paramètres afin d'apprendre ce modèle d'apprentissage automatique. De même, si nous avons 30 attributs booléens indépendants, alors le nombre total de paramètres à calculer sera proche de 3 milliards, ce qui est extrêmement élevé en coût de calcul.
Cette difficulté à construire un modèle d'apprentissage automatique avec le théorème de Bayes a conduit à la naissance et au développement de l'algorithme Naive Bayes.
Algorithme de Bayes naïf
Pour être pratique, la complexité mentionnée ci-dessus du théorème de Bayes doit être réduite. Ceci est exactement réalisé dans l'algorithme Naive Bayes en faisant peu d'hypothèses. Les hypothèses émises sont que chaque caractéristique apporte une contribution indépendante et égale au résultat.
L'algorithme naïf de Bayes est un algorithme d'apprentissage supervisé et il est basé sur le théorème de Bayes qui est principalement utilisé pour résoudre des problèmes de classification. C'est l'un des classificateurs les plus simples et les plus précis qui construisent des modèles d'apprentissage automatique pour faire des prédictions rapides. Mathématiquement, c'est un classificateur probabiliste car il fait des prédictions en utilisant la fonction de probabilité des événements.
Exemple de problème
Afin de comprendre la logique derrière les hypothèses, passons en revue un ensemble de données simple pour obtenir une meilleure intuition.
| Couleur | Taper | Origine | Vol? |
| Le noir | Sedan | Importé | Oui |
| Le noir | VUS | Importé | Non |
| Le noir | Sedan | National | Oui |
| Le noir | Sedan | Importé | Non |
| marron | VUS | National | Oui |
| marron | VUS | National | Non |
| marron | Sedan | Importé | Non |
| marron | VUS | Importé | Oui |
| marron | Sedan | National | Non |
À partir de l'ensemble de données ci-dessus, nous pouvons dériver les concepts des deux hypothèses que nous avons définies pour l'algorithme Naive Bayes ci-dessus.
- La première hypothèse est que toutes les caractéristiques sont indépendantes les unes des autres. Ici, on voit que chaque attribut est indépendant tel que la couleur "Rouge" est indépendante du Type et de l'Origine de la voiture.
- Ensuite, chaque caractéristique doit se voir accorder une importance égale. De même, avoir uniquement des connaissances sur le type et l'origine de la voiture n'est pas suffisant pour prédire la sortie du problème. Par conséquent, aucune des variables n'est non pertinente et, par conséquent, elles apportent toutes une contribution égale au résultat.
Pour résumer, A et B sont conditionnellement indépendants étant donné C si et seulement si, sachant que C se produit, savoir si A se produit ne fournit aucune information sur la probabilité que B se produise, et savoir si B se produit ne fournit aucune information sur la probabilité que A se produise. Ces hypothèses rendent l'algorithme de Bayes – Naive . D'où le nom, Naive Bayes Algorithm.
Par conséquent, pour le problème ci-dessus, le théorème de Bayes peut être réécrit comme -
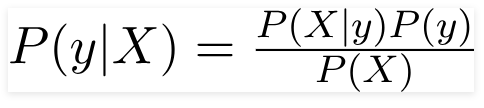
Tel que,
- Le vecteur de caractéristiques indépendant, X = (x 1 , x 2 , x 3 ……x n ) représentant les caractéristiques telles que la couleur, le type et l'origine de la voiture.
- La variable de sortie, y n'a que deux résultats Oui ou Non.
Par conséquent, en substituant les valeurs ci-dessus, nous obtenons la formule naïve de Bayes comme,
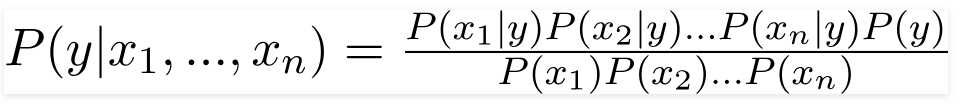
Afin de calculer la probabilité postérieure P(y|X), nous devons créer un tableau de fréquence pour chaque attribut par rapport à la sortie. Convertir ensuite les tableaux de fréquence en tableaux de probabilité, après quoi nous utilisons enfin l'équation bayésienne naïve pour calculer la probabilité a posteriori pour chaque classe. La classe avec la probabilité a posteriori la plus élevée est choisie comme résultat de la prédiction. Vous trouverez ci-dessous les tableaux de fréquence et de vraisemblance pour les trois prédicteurs.
Tableau de fréquence de la couleur Tableau de probabilité de la couleur
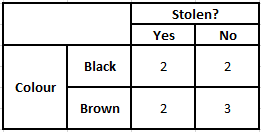
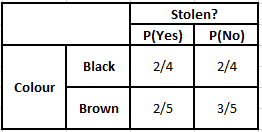
Tableau de fréquence du type Tableau de probabilité du type

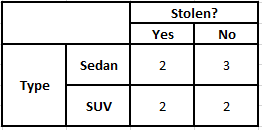
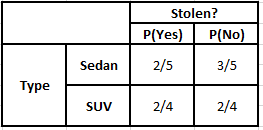
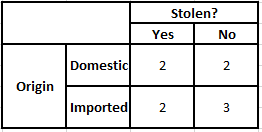
Tableau d'origine des fréquences Tableau d'origine des probabilités
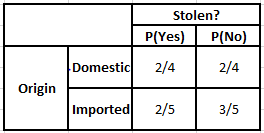
Considérons le cas où nous devons calculer les probabilités a posteriori pour les conditions ci-dessous -
| Couleur | Taper | Origine |
| marron | VUS | Importé |
Ainsi, à partir de la formule donnée ci-dessus, nous pouvons calculer les probabilités postérieures comme indiqué ci-dessous–
P(Oui | X) = P(Marron | Oui) * P(SUV | Oui) * P(Importé | Oui) * P(Oui)
= 2/5 * 2/4 * 2/5 * 1
= 0,08
P(Non | X) = P(Marron | Non) * P(SUV | Non) * P(Importé | Non) * P(Non)
= 3/5 * 2/4 * 3/5 * 1
= 0,18
À partir des valeurs calculées ci-dessus, étant donné que les probabilités postérieures pour Non sont supérieures à Oui (0,18>0,08), on peut en déduire qu'une voiture de couleur marron, type SUV d'origine importée, est classée comme "Non". La voiture n'est donc pas volée.
Implémentation en Python
Maintenant que nous avons compris les mathématiques derrière l'algorithme Naive Bayes et que nous l'avons également visualisé avec un exemple, passons en revue son code d'apprentissage automatique en langage Python.
En relation: Classificateur naïf de Bayes
Analyse du problème
Afin d'implémenter le programme Naive Bayes Classification en Machine Learning à l'aide de Python, nous utiliserons le très célèbre 'Iris Flower Dataset'. L'ensemble de données sur les fleurs d'iris ou l'ensemble de données sur l'iris de Fisher est un ensemble de données multivariées introduit par le statisticien, eugéniste et biologiste britannique Ronald Fisher en 1998. Il s'agit d'un très petit ensemble de données de base composé de très peu de données numériques contenant des informations sur 3 classes de fleurs appartenant à l'espèce Iris qui sont -
- Iris Setosa
- Iris Versicolor
- Iris de Virginie
Il y a 50 échantillons de chacune des trois espèces, ce qui représente un ensemble de données total de 150 lignes. Les 4 attributs (ou) variables indépendantes utilisées dans cet ensemble de données sont -
- longueur des sépales en cm
- largeur des sépales en cm
- longueur des pétales en cm
- largeur des pétales en cm
La variable dépendante est « l' espèce » de la fleur qui est identifiée par les quatre attributs ci-dessus.
Étape 1 - Importation des bibliothèques
Comme toujours, la première étape de la création d'un modèle d'apprentissage automatique consistera à importer les bibliothèques pertinentes. Pour cela, nous allons charger les librairies NumPy, Mathplotlib et Pandas pour pré-traiter les données.
importer numpy en tant que np
importer matplotlib.pyplot en tant que plt
importer des pandas en tant que pd
Étape 2 - Chargement de l'ensemble de données
L'ensemble de données de fleurs d'iris à utiliser pour la formation du classificateur Naive Bayes doit être chargé dans un DataFrame Pandas. Les 4 variables indépendantes doivent être affectées à la variable X et la variable d'espèce de sortie finale est affectée à y.
jeu de données = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = jeu de données.iloc[:,:4].values
y = dataset['species'].valuesdataset.head(5)>>
sépale_longueur sépale_largeur pétale_longueur pétale_largeur espèce
5,1 3,5 1,4 0,2 setosa
4,9 3,0 1,4 0,2 setosa
4,7 3,2 1,3 0,2 setosa
4,6 3,1 1,5 0,2 setosa
5,0 3,6 1,4 0,2 setosa
Étape 3 - Fractionnement de l'ensemble de données dans l'ensemble d'apprentissage et l'ensemble de test
Après avoir chargé l'ensemble de données et les variables, l'étape suivante consiste à préparer les variables qui subiront le processus de formation. Dans cette étape, nous devons diviser les variables X et y entre l'apprentissage et les jeux de données de test. Pour cela, nous attribuerons 80 % des données de manière aléatoire à l'ensemble d'apprentissage qui sera utilisé à des fins d'entraînement et les 20 % restants des données comme ensemble de test sur lequel le classificateur Naive Bayes formé sera testé pour la précision.
depuis sklearn.model_selection importer train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Étape 4 - Mise à l'échelle des fonctionnalités
Bien qu'il s'agisse d'un processus supplémentaire à ce petit ensemble de données, je l'ajoute pour que vous puissiez l'utiliser dans un ensemble de données plus grand. Dans ce cas, les données des ensembles d'apprentissage et de test sont réduites à une plage de valeurs comprises entre 0 et 1. Cela réduit le coût de calcul.
depuis sklearn.preprocessing importer StandardScaler
sc = Échelle Standard()
X_train = sc.fit_transform(X_train)
X_test = sc.transform(X_test)
Étape 5 - Entraînement du modèle de classification Naive Bayes sur l'ensemble d'entraînement
C'est dans cette étape que nous importons la classe Naive Bayes de la bibliothèque sklearn. Pour ce modèle, nous utilisons le modèle Gaussien, il existe plusieurs autres modèles tels que Bernoulli, Catégorique et Multinomial. Ainsi, X_train et y_train sont ajustés à la variable de classificateur à des fins de formation.
de sklearn.naive_bayes importer GaussianNB
classifieur = GaussianNB()
classifier.fit(X_train, y_train)
Étape 6 - Prédire les résultats de l'ensemble de test -
Nous prédisons la classe de l'espèce pour l'ensemble de test à l'aide du modèle formé et la comparons avec les valeurs réelles de la classe d'espèces.
y_pred = classifier.predict(X_test)
df = pd.DataFrame({'Valeurs réelles':y_test, 'Valeurs prédites':y_pred})
df>>
Valeurs réelles Valeurs prédites
setosa setosa
setosa setosa
virginie virginie
versicolore versicolore
setosa setosa
setosa setosa
… … … … …
virginica versicolor
virginie virginie
setosa setosa
setosa setosa
versicolore versicolore
versicolore versicolore
Dans la comparaison ci-dessus, nous voyons qu'il y a une prédiction incorrecte qui a prédit Versicolor au lieu de virginica.
Étape 7 - Matrice de confusion et précision
Comme nous traitons de la classification, la meilleure façon d'évaluer notre modèle de classificateur est d'imprimer la matrice de confusion avec sa précision sur l'ensemble de test.
depuis sklearn.metrics importer confusion_matrix
cm = confusion_matrix (y_test, y_pred) de sklearn.metrics import precision_score

print (“Précision : “, precision_score(y_test, y_pred))
cm>>Précision : 0.9666666666666667
>>tableau([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
Conclusion
Ainsi, dans cet article, nous avons passé en revue les bases de l'algorithme Naive Bayes, compris les mathématiques derrière la classification avec un exemple résolu à la main. Enfin, nous avons implémenté un code d'apprentissage automatique pour résoudre un ensemble de données populaire à l'aide de l'algorithme Naive Bayes Classification.
Si vous souhaitez en savoir plus sur l'IA, l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, Statut d'ancien de l'IIIT-B, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.
En quoi la probabilité est-elle utile dans l'apprentissage automatique ?
Nous pouvons être amenés à prendre des décisions basées sur des informations partielles ou incomplètes dans des scénarios réels. La probabilité nous aide à quantifier les incertitudes dans de tels systèmes et à gérer le risque pour la tâche. La méthode traditionnelle ne fonctionne que pour les résultats déterministes d'actions spécifiques, mais il y a toujours une part d'incertitude dans tout modèle de prédiction. Cette incertitude peut provenir de nombreux paramètres des données d'entrée, tels que le bruit dans les données. De plus, les vues bayésiennes des théorèmes de probabilité peuvent aider à la reconnaissance de formes à partir des données d'entrée. Pour cela, la probabilité utilise le concept d'estimation du maximum de vraisemblance et est donc utile pour produire des résultats pertinents.
A quoi sert la matrice de confusion ?
La matrice de confusion est une matrice 2x2 utilisée pour interpréter les performances du modèle de classification. Les vraies valeurs des données d'entrée doivent être connues pour que cela fonctionne, de sorte qu'elles ne peuvent pas être représentées pour les données sans étiquette. Il se compose du nombre de faux positifs (FP), de vrais positifs (TP), de faux négatifs (FN) et de vrais négatifs (TN). Les prédictions sont classées dans ces classes à l'aide du décompte de l'ensemble d'apprentissage et de l'ensemble de test. Il nous aide à visualiser des paramètres utiles tels que l'exactitude, la précision, le rappel et la spécificité. Il est relativement facile à comprendre et vous donne une idée claire de l'algorithme.
Quels sont les différents types de modèle Naive Bayes ?
Tous les types sont principalement basés sur le théorème de Bayes. Le modèle Naive Bayes a généralement trois types : Gaussien, Bernoulli et Multinomial. Le Gaussian Naive Bayes aide avec des valeurs continues à partir des paramètres d'entrée, et il suppose que toutes les classes de données d'entrée sont uniformément distribuées. Le Bayes naïf de Bernoulli est un modèle basé sur les événements où les caractéristiques des données sont indépendantes et présentes dans des valeurs booléennes. Multinomial Naive Bayes est également basé sur un modèle événementiel. Il contient les caractéristiques des données sous forme vectorielle, qui représentent les fréquences pertinentes en fonction de l'occurrence des événements.
