7 algorithmes d'apprentissage automatique les plus utilisés en Python que vous devriez connaître

L'apprentissage automatique est une branche de l'intelligence artificielle (IA) qui traite des algorithmes informatiques utilisés sur toutes les données. Il se concentre sur l'apprentissage automatique à partir des données qui y sont introduites et il nous donne des résultats en améliorant à chaque fois les prédictions précédentes.

Principaux algorithmes d'apprentissage automatique utilisés en Python

Vous trouverez ci-dessous quelques-uns des meilleurs algorithmes d'apprentissage automatique utilisés dans Python, ainsi que des extraits de code montrant leur implémentation et des visualisations des limites de classification.

1. Régression linéaire

La régression linéaire est l'une des techniques d'apprentissage automatique supervisé les plus couramment utilisées. Comme son nom l'indique, cette régression tente de modéliser la relation entre deux variables à l'aide d'une équation linéaire et d'ajuster cette ligne aux données observées. Cette technique est utilisée pour estimer des valeurs continues réelles telles que le total des ventes réalisées ou le coût des maisons.

La droite de meilleur ajustement est aussi appelée droite de régression. Elle est donnée par l'équation suivante :

Y = a*X + b

où Y est la variable dépendante, a est la pente, X est la variable indépendante et b est la valeur d'interception. Les coefficients a et b sont dérivés en minimisant le carré de la différence de cette distance entre les divers points de données et l'équation de la droite de régression.

# ensemble de données synthétiques pour la régression simple

à partir de sklearn.datasets importer make_regression

plt.figure()

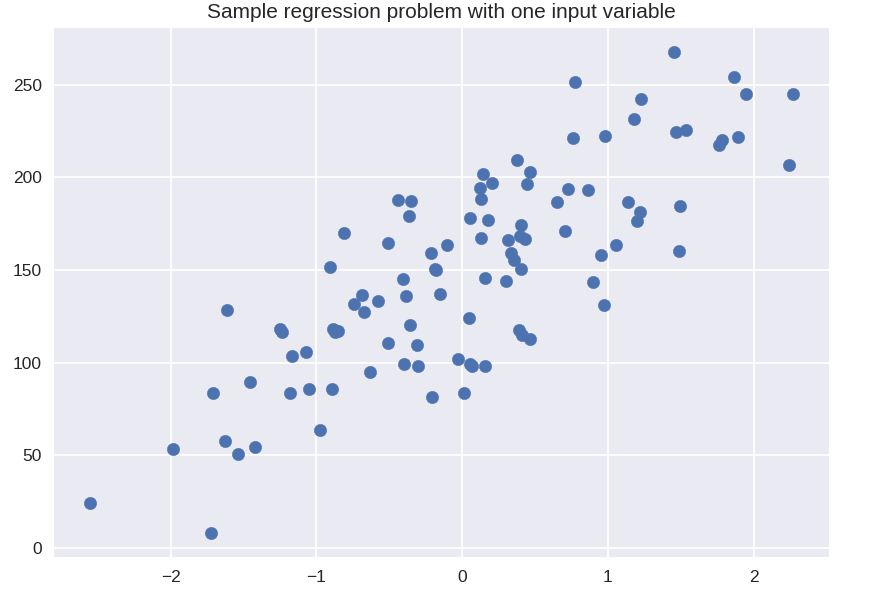
plt.title( 'Problème de régression d'échantillon avec une variable d'entrée' )

X_R1, y_R1 = make_regression( n_samples = 100, n_features = 1, n_informative = 1, bias = 150.0, noise = 30, random_state = 0 )

plt.scatter( X_R1, y_R1, marqueur = 'o', s = 50 )

plt.show()

de sklearn.linear_model importer LinearRegression

X_train, X_test, y_train, y_test = train_test_split( X_R1, y_R1,

état_aléatoire = 0 )

linreg = LinearRegression().fit( X_train, y_train )

print( 'coeff du modèle linéaire (w): {}'.format( linreg.coef_ ) )

print( 'interception du modèle linéaire (b): {:.3f}'z.format( linreg.intercept_ ) )

print( 'Score R-carré (entraînement) : {:.3f}'.format( linreg.score( X_train, y_train ) ) )

print( 'Score R-carré (test): {:.3f}'.format( linreg.score( X_test, y_test ) ) )

Sortir

modèle linéaire coeff (w) : [ 45,71]

Interception du modèle linéaire (b) : 148,446

Score R au carré (entraînement) : 0,679

Score R au carré (test) : 0,492

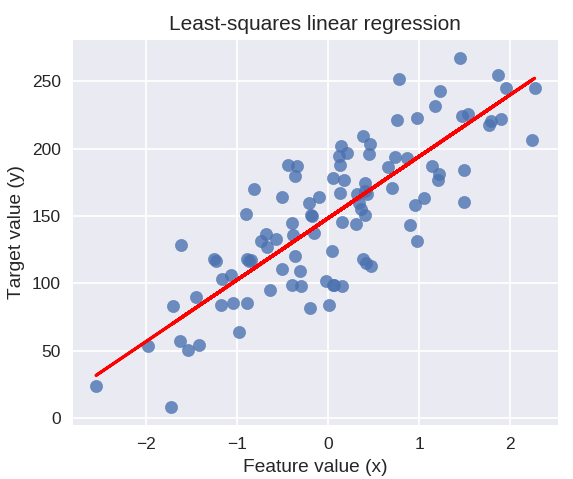
Le code suivant tracera la ligne de régression ajustée sur le tracé de nos points de données.

plt.figure( figsize = ( 5, 4 ) )

plt.scatter( X_R1, y_R1, marqueur = 'o', s = 50, alpha = 0.8 )

plt.plot( X_R1, linreg.coef_ * X_R1 + linreg.intercept_, 'r-' )

plt.title( 'Régression linéaire des moindres carrés' )

plt.xlabel( 'Valeur caractéristique (x)' )

plt.ylabel( 'Valeur cible (y)' )

plt.show()

Préparation d'un ensemble de données commun pour l'exploration des techniques de classification

Les données suivantes vont être utilisées pour montrer les différents algorithmes de classification les plus couramment utilisés dans l'apprentissage automatique en Python.

L' ensemble de données UCI Mushroom est stocké dans champignons.csv.

bloc-notes %matplotlib

importer des pandas en tant que pd

importer numpy en tant que np

importer matplotlib.pyplot en tant que plt

depuis sklearn.decomposition import PCA

depuis sklearn.model_selection importer train_test_split

df = pd.read_csv( 'lecture seule/champignons.csv' )

df2 = pd.get_dummies( df )

df3 = df2.sample( frac = 0.08 )

X = df3.iloc[:, 2:]

y = df3.iloc[:, 1]

pca = PCA( n_composants = 2 ).fit_transform( X )

X_train, X_test, y_train, y_test = train_test_split( pca, y, random_state = 0 )

plt.figure( dpi = 120 )

plt.scatter( pca[y.values ​​== 0, 0], pca[y.values ​​== 0, 1], alpha = 0.5, label = 'Comestible', s = 2 )

plt.scatter( pca[y.values ​​== 1, 0], pca[y.values ​​== 1, 1], alpha = 0.5, label = 'Poisonous', s = 2 )

plt.légende()

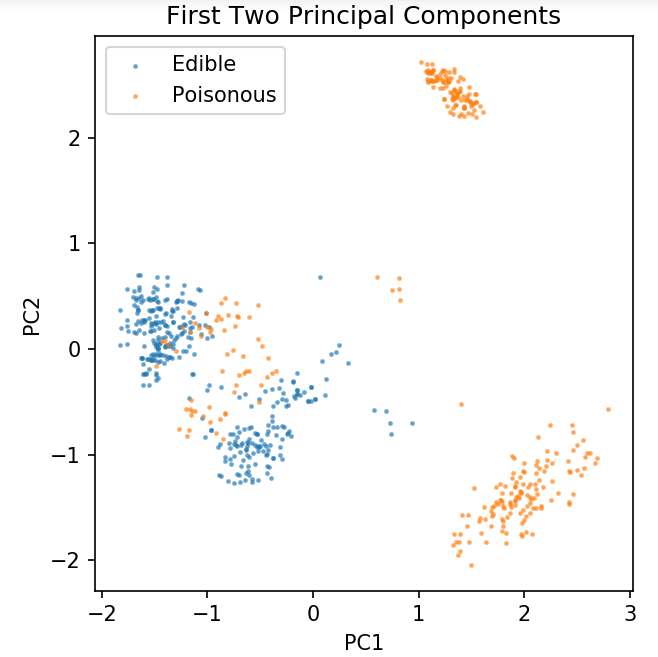
plt.title( 'Ensemble de données de champignons\nDeux premiers composants principaux' )

plt.xlabel( 'PC1' )

plt.ylabel( 'PC2' )

plt.gca().set_aspect( 'égal' )

Nous utiliserons la fonction définie ci-dessous pour obtenir les limites de décision des différents classificateurs que nous utiliserons sur l'ensemble de données de champignons.

def plot_mushroom_boundary( X, y, modèle_ajusté ):

plt.figure( figsize = (9.8, 5), dpi = 100 )

pour moi, plot_type in enumerate( ['Decision Boundary', 'Decision Probabilities'] ):

plt.subplot( 1, 2, je + 1 )

mesh_step_size = 0.01 # taille du pas dans le maillage

x_min, x_max = X[:, 0].min() – .1, X[:, 0].max() + .1

y_min, y_max = X[:, 1].min() – .1, X[:, 1].max() + .1

xx, yy = np.meshgrid( np.arange( x_min, x_max, mesh_step_size ), np.arange( y_min, y_max, mesh_step_size ) )

si je == 0 :

Z = modèle_équipé.prédire( np.c_[xx.ravel(), yy.ravel()] )

autre:

essayer:

Z = modèle_équipé.predict_proba( np.c_[xx.ravel(), yy.ravel()] )[:, 1]

à l'exception:

plt.text( 0.4, 0.5, 'Probabilités indisponibles', horizontalalignment = 'center', verticalalignment = 'center', transform = plt.gca().transAxes, fontsize = 12 )

plt.axis( 'off' )

Pause

Z = Z.reshape( xx.forme )

plt.scatter( X[y.values ​​== 0, 0], X[y.values ​​== 0, 1], alpha = 0.4, label = 'Comestible', s = 5 )

plt.scatter( X[y.values ​​== 1, 0], X[y.values ​​== 1, 1], alpha = 0.4, label = 'Posionous', s = 5 )

plt.imshow( Z, interpolation = 'le plus proche', cmap = 'RdYlBu_r', alpha = 0.15, extent = ( x_min, x_max, y_min, y_max ), origin = 'lower' )

plt.title( type_intrigue + '\n' + str( modèle_ajusté ).split( '(' )[0] + ' Précision du test : ' + str( np.round( modèle_ajusté.score( X, y ), 5 ) ) )

plt.gca().set_aspect( 'equal' );

plt.tight_layout()

plt.subplots_adjust( haut = 0.9, bas = 0.08, wspace = 0.02 )

2. Régression logistique

Contrairement à la régression linéaire, la régression logistique traite de l'estimation de valeurs discrètes (valeurs binaires 0/1, vrai/faux, oui/non). Cette technique est également appelée régression logit. En effet, il prédit la probabilité d'un événement en utilisant une fonction logit pour former les données données. Sa valeur est toujours comprise entre 0 et 1 (puisqu'il calcule une probabilité).

La probabilité logarithmique des résultats est construite comme une combinaison linéaire de la variable prédictive comme suit :

cotes = p / (1 – p) = probabilité qu'un événement se produise ou probabilité qu'un événement ne se produise pas

ln( cotes ) = ln( p / (1 – p) )

logit( p ) = ln( p / (1 – p) ) = b0 + b1X1 + b2X2 + b3X3 + … + bkXk

où p est la probabilité de présence d'une caractéristique.

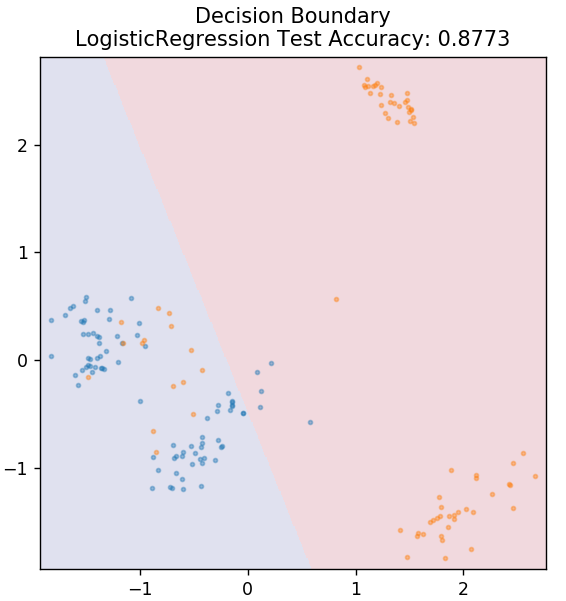
de sklearn.linear_model importer LogisticRegression

modèle = LogisticRegression()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

Obtenez une certification en intelligence artificielle en ligne auprès des meilleures universités du monde - Masters, Executive Post Graduate Programs et Advanced Certificate Program in ML & AI pour accélérer votre carrière.

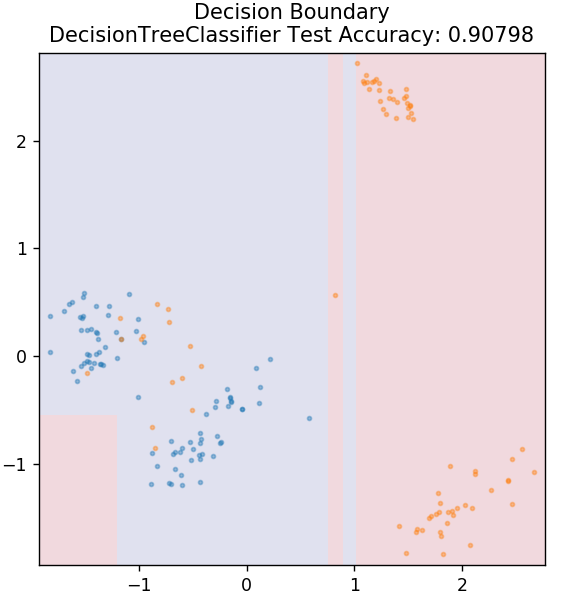
3. Arbre de décision

Il s'agit d'un algorithme très populaire qui peut être utilisé pour classer à la fois des variables continues et discrètes de données. À chaque étape, les données sont divisées en plusieurs ensembles homogènes en fonction de certains attributs/conditions de division.

depuis sklearn.tree importer DecisionTreeClassifier

modèle = DecisionTreeClassifier( max_depth = 3 )

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

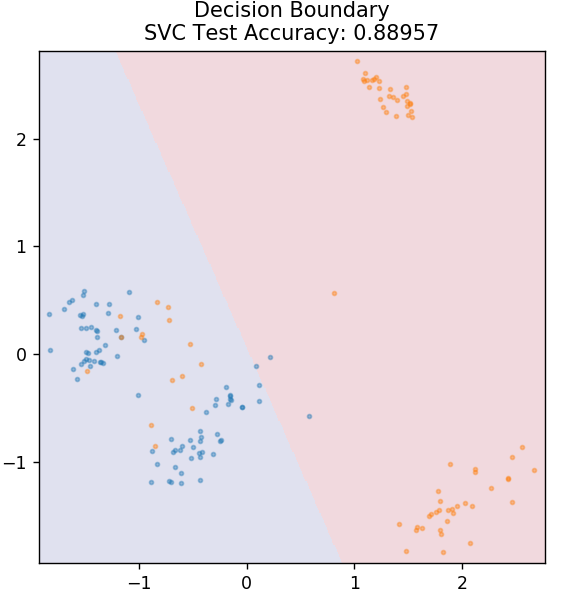
4. SVM

SVM est l'abréviation de Support Vector Machines. Ici, l'idée de base est de classer les points de données en utilisant des hyperplans pour la séparation. L'objectif est de trouver un tel hyperplan qui a la distance maximale (ou marge) entre les points de données des classes ou des catégories.

Nous choisissons l'avion de manière à prendre soin de classer les points inconnus à l'avenir avec la plus grande confiance. Les SVM sont réputés pour leur grande précision tout en consommant très peu de puissance de calcul. Les SVM peuvent également être utilisés pour les problèmes de régression.

depuis sklearn.svm importer SVC

modèle = SVC( noyau = 'linéaire' )

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

Paiement : projets Python sur GitHub

5. Bayes naïf

Comme son nom l'indique, l'algorithme Naive Bayes est un algorithme d'apprentissage supervisé basé sur le théorème de Bayes . Le théorème de Bayes utilise des probabilités conditionnelles pour vous donner la probabilité d'un événement basé sur une connaissance donnée.

Où,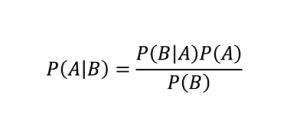

P (A | B) : la probabilité conditionnelle que l'événement A se produise, étant donné que l'événement B s'est déjà produit. (Aussi appelée probabilité postérieure)

P(A) : Probabilité de l'événement A.

P(B) : Probabilité de l'événement B.

P (B | A) : la probabilité conditionnelle que l'événement B se produise, étant donné que l'événement A s'est déjà produit.

Pourquoi cet algorithme s'appelle-t-il Naive, demandez-vous ? En effet, il suppose que toutes les occurrences d'événements sont indépendantes les unes des autres. Ainsi, chaque caractéristique définit séparément la classe à laquelle appartient un point de données, sans avoir de dépendances entre elles. Naive Bayes est le meilleur choix pour les catégorisations de texte. Cela fonctionnera suffisamment bien même avec de petites quantités de données d'entraînement.

de sklearn.naive_bayes importer GaussianNB

modèle = GaussienNB()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

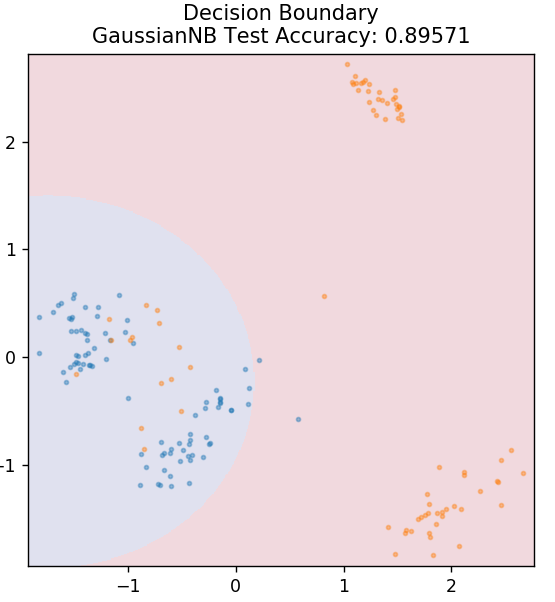
5. KN

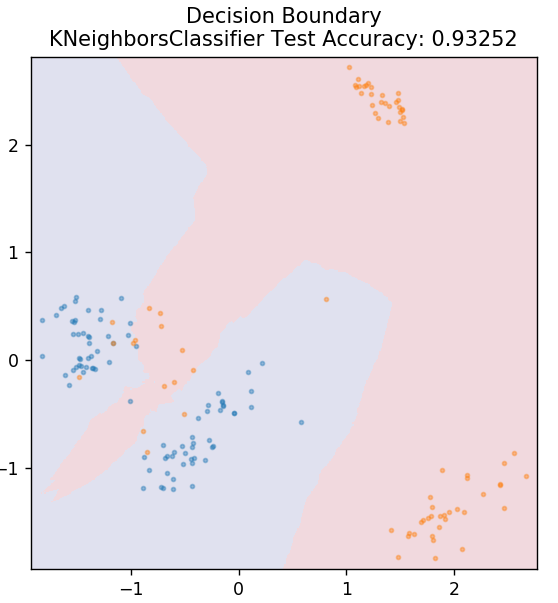
KNN signifie K-Nearest Neighbours. Il s'agit d'un algorithme d'apprentissage supervisé très largement utilisé qui classe les données de test en fonction de leurs similitudes avec les données d'apprentissage précédemment classées. KNN ne classe pas tous les points de données pendant la formation. Au lieu de cela, il stocke simplement l'ensemble de données et lorsqu'il obtient de nouvelles données, il classe ensuite ces points de données en fonction de leurs similitudes. Pour ce faire, il calcule la distance euclidienne du nombre K de voisins les plus proches (ici, n_neighbors ) de ce point de données.

de sklearn.neighbors importer KNeighborsClassifier

modèle = KNeighborsClassifier( n_neighbors = 20 )

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

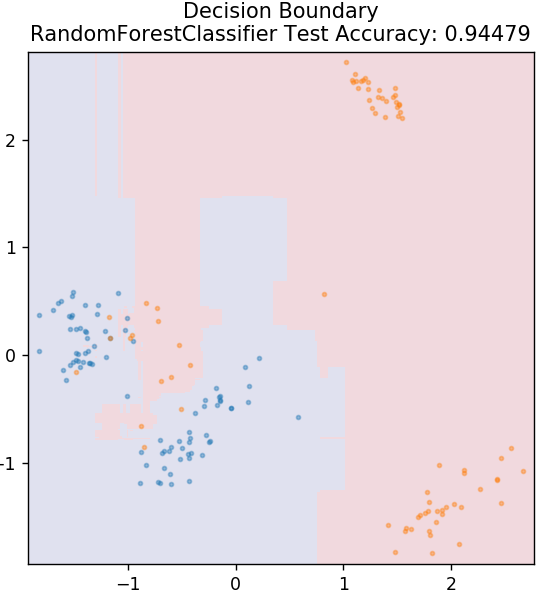
6. Forêt aléatoire

La forêt aléatoire est un algorithme d'apprentissage automatique très simple et diversifié qui utilise une technique d'apprentissage supervisé. Comme vous pouvez le deviner d'après son nom, la forêt aléatoire se compose d'un grand nombre d'arbres de décision, agissant comme un ensemble. Chaque arbre de décision déterminera la classe de sortie des points de données et la classe majoritaire sera choisie comme sortie finale du modèle. L'idée ici est que plus d'arbres travaillant sur les mêmes données auront tendance à être plus précis dans les résultats que les arbres individuels.

de sklearn.ensemble importer RandomForestClassifier

modèle = RandomForestClassifier()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

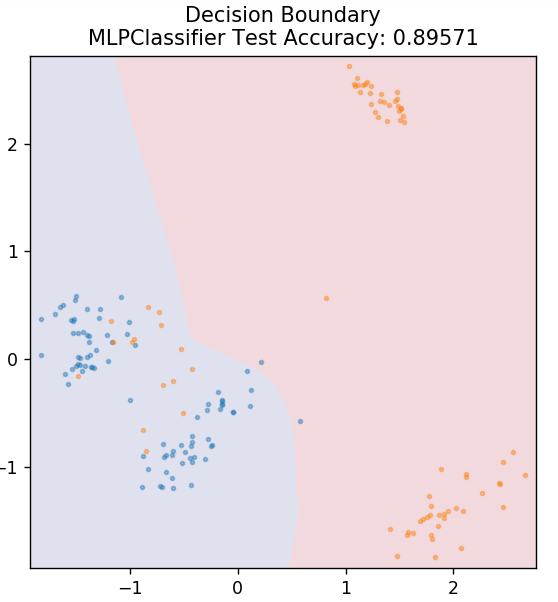
7. Perceptron multicouche

Le Perceptron multicouche (ou MLP) est un algorithme très fascinant relevant de la branche de l'apprentissage en profondeur. Plus précisément, il appartient à la classe des réseaux de neurones artificiels (ANN) feed-forward. MLP forme un réseau de plusieurs perceptrons avec au moins trois couches : une couche d'entrée, une couche de sortie et une ou plusieurs couches cachées. Les MLP sont capables de distinguer les données non linéairement séparables.

Chaque neurone des couches cachées utilise une fonction d'activation pour passer à la couche suivante. Ici, l'algorithme de rétropropagation est utilisé pour régler réellement les paramètres et donc former le réseau de neurones. Il peut principalement être utilisé pour des problèmes de régression simples.

de sklearn.neural_network importer MLPClassifier

modèle = MLPClassifier()

model.fit( X_train, y_train )

plot_mushroom_boundary( X_test, y_test, model )

Lisez également : Idées et sujets de projet Python

Conclusion

Nous pouvons conclure que différents algorithmes d'apprentissage automatique produisent des limites de décision différentes et donc des résultats de précision différents dans la classification du même ensemble de données.

Il n'y a aucun moyen de déclarer un algorithme quelconque comme le meilleur algorithme pour toutes sortes de données en général. L'apprentissage automatique nécessite des essais et des erreurs rigoureux pour divers algorithmes afin de déterminer ce qui fonctionne le mieux pour chaque ensemble de données séparément. La liste des algorithmes ML ne s'arrête évidemment pas là. Il existe une vaste mer d'autres techniques qui attendent d'être explorées dans la bibliothèque Scikit-Learn de Python. Allez-y et entraînez vos ensembles de données en utilisant tout cela et amusez-vous !

Si vous souhaitez en savoir plus sur les arbres de décision, l'apprentissage automatique, consultez le programme Executive PG d'IIIT-B & upGrad en apprentissage automatique et IA , conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et affectations, statut IIIT-B Alumni, 5+ projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.