25 questions et réponses d'entrevue sur l'apprentissage automatique - Régression linéaire
Publié: 2022-09-08Il est courant de tester les aspirants en science des données sur des algorithmes d'apprentissage automatique couramment utilisés lors d'entretiens. Ces algorithmes conventionnels étant la régression linéaire, la régression logistique, le clustering, les arbres de décision, etc. Les data scientists doivent posséder une connaissance approfondie de ces algorithmes.
Nous avons consulté des responsables du recrutement et des data scientists de diverses organisations pour connaître les questions typiques de ML qu'ils posent lors d'un entretien. Sur la base de leurs nombreux commentaires, un ensemble de questions et de réponses a été préparé pour aider les aspirants scientifiques des données dans leurs conversations. Les questions d'entretien de régression linéaire sont les plus courantes dans les entretiens d'apprentissage automatique. Des questions-réponses sur ces algorithmes seront fournies dans une série de quatre articles de blog.
Meilleurs cours d'apprentissage automatique et cours d'IA en ligne
| Master of Science en apprentissage automatique et IA de LJMU | Programme de troisième cycle exécutif en apprentissage automatique et IA de l'IIITB | |
| Programme de certificat avancé en apprentissage automatique et PNL de l'IIITB | Programme de certificat avancé en apprentissage automatique et apprentissage en profondeur de l'IIITB | Programme exécutif de troisième cycle en science des données et apprentissage automatique de l'Université du Maryland |
| Pour explorer tous nos cours, visitez notre page ci-dessous. | ||
| Cours d'apprentissage automatique | ||
Chaque article de blog couvrira le sujet suivant : -
- Régression linéaire
- Régression logistique
- Regroupement
- Arbres de décision et questions concernant tous les algorithmes
Commençons par la régression linéaire !
1. Qu'est-ce que la régression linéaire ?
En termes simples, la régression linéaire est une méthode pour trouver le meilleur ajustement de ligne droite aux données données, c'est-à-dire trouver la meilleure relation linéaire entre les variables indépendantes et dépendantes.
En termes techniques, la régression linéaire est un algorithme d'apprentissage automatique qui trouve la meilleure relation d'ajustement linéaire sur des données données, entre des variables indépendantes et dépendantes. Cela se fait principalement par la méthode de la somme des résidus au carré.
Compétences en apprentissage automatique en demande
| Cours d'intelligence artificielle | Cours Tableaux |
| Cours PNL | Cours d'apprentissage en profondeur |

2. Énoncez les hypothèses dans un modèle de régression linéaire.
Il existe trois hypothèses principales dans un modèle de régression linéaire :
- L'hypothèse sur la forme du modèle :
On suppose qu'il existe une relation linéaire entre les variables dépendantes et indépendantes. C'est ce qu'on appelle « l'hypothèse de linéarité ». - Hypothèses sur les résidus :
- Hypothèse de normalité : On suppose que les termes d'erreur, ε (i) , sont normalement distribués.
- Hypothèse de moyenne nulle : On suppose que les résidus ont une valeur moyenne de zéro.
- Hypothèse de variance constante : On suppose que les termes résiduels ont la même variance (mais inconnue), σ 2 Cette hypothèse est également connue sous le nom d'hypothèse d'homogénéité ou d'homoscédasticité.
- Hypothèse d'erreur indépendante : On suppose que les termes résiduels sont indépendants les uns des autres, c'est-à-dire que leur covariance par paire est nulle.
- Hypothèses sur les estimateurs :
- Les variables indépendantes sont mesurées sans erreur.
- Les variables indépendantes sont linéairement indépendantes les unes des autres, c'est-à-dire qu'il n'y a pas de multicolinéarité dans les données.
Explication:
- Cela va de soi.
- Si les résidus ne sont pas distribués normalement, leur caractère aléatoire est perdu, ce qui implique que le modèle n'est pas en mesure d'expliquer la relation dans les données.
De plus, la moyenne des résidus doit être nulle.
Y (i)i = β 0 + β 1 x (i) + ε (i)
Il s'agit du modèle linéaire supposé, où ε est le terme résiduel.
E(Y) = E( β 0 + β 1 X (i) + ε (i) )
= E( β 0 + β 1 X (i) + ε (i) )
Si l'espérance (moyenne) des résidus, E(ε (i) ), est nulle, les attentes de la variable cible et du modèle deviennent identiques, ce qui est l'une des cibles du modèle.
Les résidus (également appelés termes d'erreur) doivent être indépendants. Cela signifie qu'il n'y a pas de corrélation entre les résidus et les valeurs prédites, ou entre les résidus eux-mêmes. Si une certaine corrélation est présente, cela implique qu'il existe une relation que le modèle de régression n'est pas en mesure d'identifier. - Si les variables indépendantes ne sont pas linéairement indépendantes les unes des autres, l'unicité de la solution des moindres carrés (ou solution de l'équation normale) est perdue.
Rejoignez le cours d'intelligence artificielle en ligne des meilleures universités du monde - Masters, Executive Post Graduate Programs et Advanced Certificate Program in ML & AI pour accélérer votre carrière.
3. Qu'est-ce que l'ingénierie des fonctionnalités ? Comment l'appliquez-vous dans le processus de modélisation?
L'ingénierie des fonctionnalités est le processus de transformation des données brutes en fonctionnalités qui représentent mieux le problème sous-jacent aux modèles prédictifs
, ce qui améliore la précision du modèle sur des données invisibles.
En termes simples, l'ingénierie des fonctionnalités signifie le développement de nouvelles fonctionnalités qui peuvent vous aider à mieux comprendre et modéliser le problème. L'ingénierie des fonctionnalités est de deux types : axée sur l'entreprise et axée sur les données. L'ingénierie des fonctionnalités axée sur l'entreprise s'articule autour de l'inclusion de fonctionnalités d'un point de vue commercial. Le travail consiste ici à transformer les variables métier en caractéristiques du problème. Dans le cas d'une ingénierie de caractéristiques basée sur les données, les caractéristiques que vous ajoutez n'ont pas d'interprétation physique significative, mais elles aident le modèle dans la prédiction de la variable cible.
Pour votre information : Cours de PNL gratuit !
Pour appliquer l'ingénierie des fonctionnalités, il faut être parfaitement familiarisé avec l'ensemble de données. Cela implique de savoir quelles sont les données données, ce qu'elles signifient, quelles sont les caractéristiques brutes, etc. Vous devez également avoir une idée claire du problème, par exemple quels facteurs affectent la variable cible, quelle est l'interprétation physique de la variable. , etc.
4. A quoi sert la régularisation ? Expliquer les régularisations L1 et L2.
La régularisation est une technique utilisée pour résoudre le problème de surajustement du modèle. Lorsqu'un modèle très complexe est implémenté sur les données d'apprentissage, il se surajuste. Parfois, le modèle simple peut ne pas être en mesure de généraliser les données et les surajustements du modèle complexe. Pour résoudre ce problème, la régularisation est utilisée.
La régularisation n'est rien d'autre que l'ajout des termes de coefficient (beta) à la fonction de coût afin que les termes soient pénalisés et soient de petite ampleur. Cela aide essentiellement à capturer les tendances dans les données et en même temps empêche le surajustement en ne laissant pas le modèle devenir trop complexe.
- Régularisation L1 ou LASSO : Ici, les valeurs absolues des coefficients sont ajoutées à la fonction de coût. Cela peut être vu dans l'équation suivante; la partie en surbrillance correspond à la régularisation L1 ou LASSO. Cette technique de régularisation donne des résultats clairsemés, ce qui conduit également à la sélection de caractéristiques.
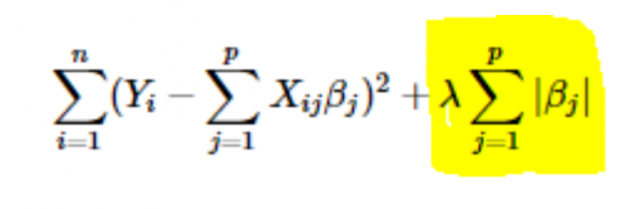
- L2 ou régularisation Ridge : Ici, les carrés des coefficients sont ajoutés à la fonction de coût. Cela peut être vu dans l'équation suivante, où la partie en surbrillance correspond à la régularisation L2 ou Ridge.
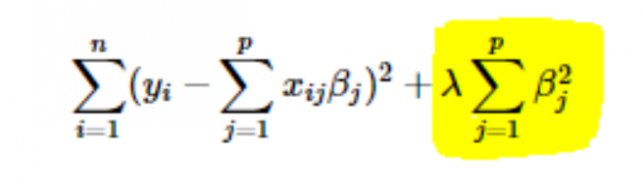
5. Comment choisir la valeur du paramètre vitesse d'apprentissage (α) ?
La sélection de la valeur du taux d'apprentissage est une affaire délicate. Si la valeur est trop petite, l'algorithme de descente de gradient met des années à converger vers la solution optimale. D'autre part, si la valeur du taux d'apprentissage est élevée, la descente de gradient dépassera la solution optimale et ne convergera probablement jamais vers la solution optimale.
Pour surmonter ce problème, vous pouvez essayer différentes valeurs d'alpha sur une plage de valeurs et tracer le coût en fonction du nombre d'itérations. Ensuite, sur la base des graphiques, la valeur correspondant au graphique montrant la décroissance rapide peut être choisie. 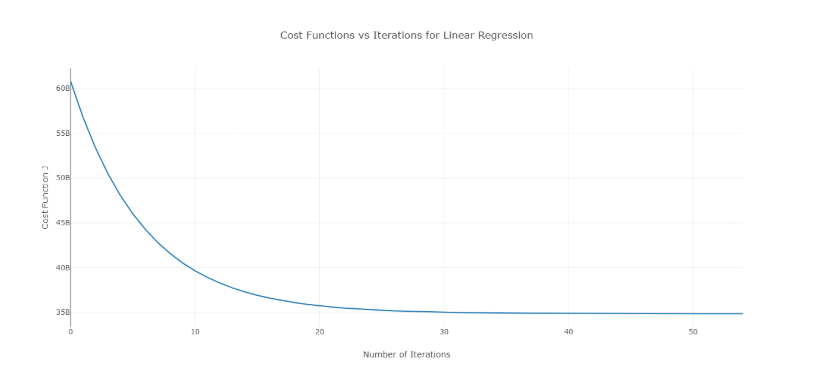
Le graphique ci-dessus est un coût idéal par rapport au nombre d'itérations. Notez que le coût diminue initialement lorsque le nombre d'itérations augmente, mais après certaines itérations, la descente de gradient converge et le coût ne diminue plus.
Si vous voyez que le coût augmente avec le nombre d'itérations, votre paramètre de taux d'apprentissage est élevé et il doit être diminué.
6. Comment choisir la valeur du paramètre de régularisation (λ) ?
La sélection du paramètre de régularisation est une affaire délicate. Si la valeur de λ est trop élevée, cela conduira à des valeurs extrêmement faibles du coefficient de régression β , ce qui conduira à un sous-ajustement du modèle (biais élevé - variance faible). En revanche, si la valeur de λ est 0 (très petit), le modèle aura tendance à surajuster les données d'apprentissage (faible biais – forte variance).
Il n'y a pas de méthode appropriée pour sélectionner la valeur de λ . Ce que vous pouvez faire, c'est avoir un sous-échantillon de données et exécuter l'algorithme plusieurs fois sur différents ensembles. Ici, la personne doit décider du degré de variance qui peut être toléré. Une fois que l'utilisateur est satisfait de la variance, cette valeur de λ peut être choisie pour l'ensemble de données complet.
Une chose à noter est que la valeur de λ sélectionnée ici était optimale pour ce sous-ensemble, pas pour l'ensemble des données d'apprentissage.
7. Pouvons-nous utiliser la régression linéaire pour l'analyse des séries chronologiques ?
On peut utiliser la régression linéaire pour l'analyse des séries chronologiques, mais les résultats ne sont pas prometteurs. Il est donc généralement déconseillé de le faire. Les raisons derrière cela sont -
- Les données de séries chronologiques sont principalement utilisées pour la prédiction de l'avenir, mais la régression linéaire donne rarement de bons résultats pour la prédiction future car elle n'est pas destinée à l'extrapolation.
- La plupart du temps, les données de séries chronologiques ont un modèle, comme pendant les heures de pointe, les périodes de fêtes, etc., qui seraient très probablement traitées comme des valeurs aberrantes dans l'analyse de régression linéaire.
8. De quelle valeur est proche la somme des résidus d'une régression linéaire ? Justifier.
Réponse La somme des résidus d'une régression linéaire est 0. La régression linéaire fonctionne sur l'hypothèse que les erreurs (résidus) sont normalement distribuées avec une moyenne de 0, c'est-à-dire
Y = β T X + ε
Ici, Y est la variable cible ou dépendante,
β est le vecteur du coefficient de régression,
X est la matrice de caractéristiques contenant toutes les caractéristiques sous forme de colonnes,
ε est le terme résiduel tel que ε ~ N(0,σ 2 ).
Ainsi, la somme de tous les résidus est la valeur attendue des résidus multipliée par le nombre total de points de données. Puisque l'espérance des résidus est 0, la somme de tous les termes résiduels est nulle.
Remarque : N(μ,σ 2 ) est la notation standard pour une distribution normale ayant une moyenne μ et un écart type σ 2 .
9. Comment la multicolinéarité affecte-t-elle la régression linéaire ?
La multicolinéarité se produit lorsque certaines des variables indépendantes sont fortement corrélées (positivement ou négativement) les unes avec les autres. Cette multicolinéarité pose un problème car elle va à l'encontre de l'hypothèse de base de la régression linéaire. La présence de multicolinéarité n'affecte pas la capacité prédictive du modèle. Donc, si vous voulez juste des prédictions, la présence de multicolinéarité n'affecte pas votre sortie. Cependant, si vous souhaitez tirer des enseignements du modèle et les appliquer, disons, à un modèle commercial, cela peut entraîner des problèmes.
L'un des principaux problèmes causés par la multicolinéarité est qu'elle conduit à des interprétations incorrectes et fournit des informations erronées. Les coefficients de régression linéaire suggèrent le changement moyen de la valeur cible si une caractéristique est modifiée d'une unité. Donc, si la multicolinéarité existe, cela n'est pas vrai car la modification d'une caractéristique entraînera des changements dans la variable corrélée et des changements conséquents dans la variable cible. Cela conduit à de fausses idées et peut produire des résultats dangereux pour une entreprise.
Un moyen très efficace de traiter la multicolinéarité est l'utilisation du VIF (Variance Inflation Factor). Plus la valeur de VIF pour une caractéristique est élevée, plus cette caractéristique est linéairement corrélée. Supprimez simplement la fonctionnalité avec une valeur VIF très élevée et réentraînez le modèle sur le jeu de données restant.
10. Quelle est la forme normale (équation) de la régression linéaire ? Quand faut-il la préférer à la méthode de descente de gradient ?
L'équation normale de la régression linéaire est —
β=(X T X) -1 . X T Y
Ici, Y=β T X est le modèle de la régression linéaire,
Y est la variable cible ou dépendante,
β est le vecteur du coefficient de régression, obtenu à l'aide de l'équation normale,
X est la matrice de caractéristiques contenant toutes les caractéristiques sous forme de colonnes.
Notez ici que la première colonne de la matrice X est constituée de tous les 1. Il s'agit d'incorporer la valeur de décalage pour la droite de régression.
Comparaison entre descente de gradient et équation normale :
| Descente graduelle | Équation normale |
| Nécessite un réglage hyper-paramètre pour alpha (paramètre d'apprentissage) | Pas un tel besoin |
| C'est un processus itératif | C'est un processus non itératif |
| O(kn 2 ) complexité temporelle | O(n 3 ) complexité temporelle due à l'évaluation de X T X |
| Préféré quand n est extrêmement grand | Devient assez lent pour les grandes valeurs de n |
Ici, « k » est le nombre maximal d'itérations pour la descente de gradient, et « n » est le nombre total de points de données dans l'ensemble d'apprentissage.
De toute évidence, si nous avons de grandes données d'entraînement, l'équation normale n'est pas préférée pour l'utilisation. Pour les petites valeurs de ' n ', l'équation normale est plus rapide que la descente de gradient.
Qu'est-ce que l'apprentissage automatique et pourquoi c'est important
11. Vous exécutez votre régression sur différents sous-ensembles de vos données, et dans chaque sous-ensemble, la valeur bêta d'une certaine variable varie énormément. Quel pourrait être le problème ici?
Ce cas implique que le jeu de données est hétérogène. Ainsi, pour surmonter ce problème, l'ensemble de données doit être regroupé en différents sous-ensembles, puis des modèles distincts doivent être créés pour chaque cluster. Une autre façon de traiter ce problème consiste à utiliser des modèles non paramétriques, tels que des arbres de décision, qui peuvent traiter des données hétérogènes assez efficacement.

12. Votre régression linéaire ne s'exécute pas et indique qu'il existe un nombre infini de meilleures estimations pour les coefficients de régression. Qu'est-ce qui ne va pas ?
Cette condition survient lorsqu'il existe une corrélation parfaite (positive ou négative) entre certaines variables. Dans ce cas, il n'y a pas de valeur unique pour les coefficients et, par conséquent, la condition donnée se produit.
13. Qu'entendez-vous par R 2 ajusté ? En quoi est-il différent de R 2 ?
R 2 ajusté , tout comme R 2 , est représentatif du nombre de points situés autour de la droite de régression. Autrement dit, il montre à quel point le modèle s'adapte aux données d'apprentissage. La formule du R 2 ajusté est -
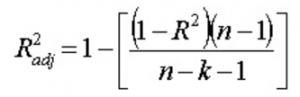
Ici, n est le nombre de points de données et k est le nombre d'entités.
Un inconvénient de R 2 est qu'il augmentera toujours avec l'ajout d'une nouvelle fonctionnalité, que la nouvelle fonctionnalité soit utile ou non. Le R 2 ajusté surmonte cet inconvénient. La valeur du R 2 ajusté n'augmente que si la caractéristique nouvellement ajoutée joue un rôle significatif dans le modèle.
14. Comment interprétez-vous la courbe de la valeur résiduelle par rapport à la valeur ajustée ?
Le diagramme des valeurs résiduelles et ajustées est utilisé pour voir si les valeurs prédites et les valeurs résiduelles ont une corrélation ou non. Si les résidus sont distribués normalement, avec une moyenne autour de la valeur ajustée et une variance constante, notre modèle fonctionne bien ; sinon, il y a un problème avec le modèle.
Le problème le plus courant que l'on peut rencontrer lors de la formation du modèle sur une large plage d'un ensemble de données est l' hétéroscédasticité (cela est expliqué dans la réponse ci-dessous). La présence d'hétéroscédasticité peut être facilement observée en traçant la courbe de la valeur résiduelle par rapport à la valeur ajustée.
15. Qu'est-ce que l'hétéroscédasticité ? Quelles sont les conséquences et comment pouvez-vous les surmonter?
Une variable aléatoire est dite hétéroscédastique lorsque différentes sous-populations ont des variabilités différentes (écart-type).
L'existence de l'hétéroscédasticité donne lieu à certains problèmes dans l'analyse de régression car l'hypothèse dit que les termes d'erreur ne sont pas corrélés et, par conséquent, la variance est constante. La présence d'hétéroscédasticité peut souvent être observée sous la forme d'un nuage de points en forme de cône pour les valeurs résiduelles par rapport aux valeurs ajustées.
L'une des hypothèses de base de la régression linéaire est que l'hétéroscédasticité n'est pas présente dans les données. En raison de la violation des hypothèses, les estimateurs des moindres carrés ordinaires (OLS) ne sont pas les meilleurs estimateurs linéaires sans biais (BLEU). Par conséquent, ils ne donnent pas le moins de variance que les autres estimateurs linéaires sans biais (LUE).
Il n'y a pas de procédure fixe pour surmonter l'hétéroscédasticité. Cependant, certains moyens peuvent conduire à une réduction de l'hétéroscédasticité. Elles sont -
- Logarithmisation des données : une série qui augmente de façon exponentielle entraîne souvent une variabilité accrue. Cela peut être surmonté en utilisant la transformation de journal.
- Utilisation de la régression linéaire pondérée : Ici, la méthode OLS est appliquée aux valeurs pondérées de X et Y. Une façon consiste à attacher des poids directement liés à l'ampleur de la variable dépendante.
16. Qu'est-ce que le VIF ? Comment le calcules-tu ?
Le facteur d'inflation de variance (VIF) est utilisé pour vérifier la présence de multicolinéarité dans un ensemble de données. Il est calculé comme—
Ici, VIF j est la valeur de VIF pour la j ème variable,
R j 2 est la valeur R 2 du modèle lorsque cette variable est régressée par rapport à toutes les autres variables indépendantes.
Si la valeur de VIF est élevée pour une variable, cela implique que le R 2 la valeur du modèle correspondant est élevée, c'est-à-dire que d'autres variables indépendantes peuvent expliquer cette variable. En termes simples, la variable dépend linéairement de certaines autres variables.
17. Comment savez-vous que la régression linéaire convient à des données données ?
Pour voir si la régression linéaire convient à des données données, un nuage de points peut être utilisé. Si la relation semble linéaire, nous pouvons opter pour un modèle linéaire. Mais si ce n'est pas le cas, nous devons appliquer quelques transformations pour rendre la relation linéaire. Le tracé des nuages de points est facile en cas de régression linéaire simple ou univariée. Mais en cas de régression linéaire multivariée, des diagrammes de dispersion bidimensionnels par paires, des diagrammes rotatifs et des graphiques dynamiques peuvent être tracés.
18. Comment les tests d'hypothèses sont-ils utilisés dans la régression linéaire ?
Les tests d'hypothèses peuvent être effectués en régression linéaire aux fins suivantes :
- Pour vérifier si un prédicteur est significatif pour la prédiction de la variable cible. Deux méthodes courantes pour cela sont -
- Par l'utilisation de p-values :
Si la valeur p d'une variable est supérieure à une certaine limite (généralement 0,05), la variable est insignifiante dans la prédiction de la variable cible. - En vérifiant les valeurs du coefficient de régression :
Si la valeur du coefficient de régression correspondant à un prédicteur est zéro, cette variable est non significative dans la prédiction de la variable cible et n'a pas de relation linéaire avec elle.
- Par l'utilisation de p-values :
- Pour vérifier si les coefficients de régression calculés sont de bons estimateurs des coefficients réels.
19. Expliquez la descente de gradient par rapport à la régression linéaire.
La descente de gradient est un algorithme d'optimisation. En régression linéaire, il est utilisé pour optimiser la fonction de coût et trouver les valeurs des βs (estimateurs) correspondant à la valeur optimisée de la fonction de coût.
La descente de gradient fonctionne comme une balle roulant sur un graphique (en ignorant l'inertie). La balle se déplace dans la direction de la plus grande pente et s'immobilise sur la surface plane (minima). 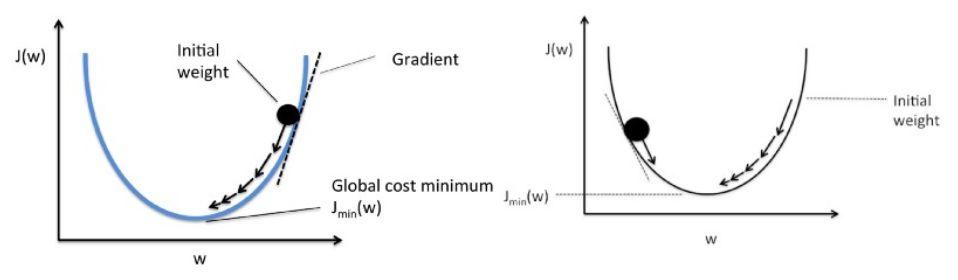
Mathématiquement, le but de la descente de gradient pour la régression linéaire est de trouver la solution de
ArgMin J(Θ 0 ,Θ 1 ), où J(Θ 0 ,Θ 1 ) est la fonction de coût de la régression linéaire. Il est donné par — 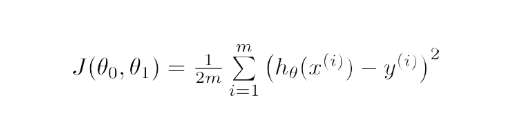
Ici, h est le modèle d'hypothèse linéaire, h=Θ 0 + Θ 1 x, y est la vraie sortie et m est le nombre de points de données dans l'ensemble d'apprentissage.
Gradient Descent commence par une solution aléatoire, puis en fonction de la direction du gradient, la solution est mise à jour à la nouvelle valeur où la fonction de coût a une valeur inférieure.
La mise à jour est :
Répéter jusqu'à convergence 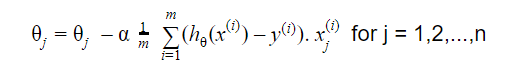
20. Comment interprétez-vous un modèle de régression linéaire ?
Un modèle de régression linéaire est assez facile à interpréter. Le modèle est de la forme suivante : 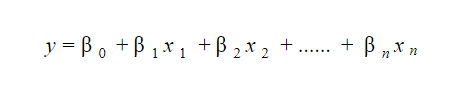
L'intérêt de ce modèle réside dans le fait que l'on peut facilement interpréter et comprendre les changements marginaux et leurs conséquences. Par exemple, si la valeur de x 0 augmente d'une unité, en gardant les autres variables constantes, l'augmentation totale de la valeur de y sera β i . Mathématiquement, le terme d'ordonnée à l'origine ( β 0 ) est la réponse lorsque tous les termes prédicteurs sont mis à zéro ou non pris en compte.
Ces 6 techniques d'apprentissage automatique améliorent les soins de santé
21. Qu'est-ce qu'une régression robuste ?
Un modèle de régression doit être de nature robuste. Cela signifie qu'avec des changements dans quelques observations, le modèle ne devrait pas changer radicalement. En outre, il ne devrait pas être très affecté par les valeurs aberrantes.
Un modèle de régression avec OLS (Ordinary Least Squares) est assez sensible aux valeurs aberrantes. Pour pallier ce problème, on peut utiliser la méthode WLS (Weighted Least Squares) pour déterminer les estimateurs des coefficients de régression. Ici, moins de poids sont donnés aux valeurs aberrantes ou aux points de levier élevés dans l'ajustement, ce qui rend ces points moins percutants.
22. Quels sont les graphiques qu'il est suggéré d'observer avant l'ajustement du modèle ?
Avant d'ajuster le modèle, il faut bien connaître les données, telles que les tendances, la distribution, l'asymétrie, etc. dans les variables. Des graphiques tels que des histogrammes, des boîtes à moustaches et des diagrammes à points peuvent être utilisés pour observer la distribution des variables. En dehors de cela, il faut également analyser quelle est la relation entre les variables dépendantes et indépendantes. Cela peut être fait par des diagrammes de dispersion (en cas de problèmes univariés), des diagrammes rotatifs, des diagrammes dynamiques, etc.
23. Qu'est-ce que le modèle linéaire généralisé ?
Le modèle linéaire généralisé est le dérivé du modèle de régression linéaire ordinaire. GLM est plus flexible en termes de résidus et peut être utilisé là où la régression linéaire ne semble pas appropriée. GLM permet à la distribution des résidus d'être autre qu'une distribution normale. Il généralise la régression linéaire en permettant au modèle linéaire de se lier à la variable cible à l'aide de la fonction de liaison. L'estimation du modèle est effectuée à l'aide de la méthode d'estimation du maximum de vraisemblance.
24. Expliquez le compromis biais-variance.
Le biais fait référence à la différence entre les valeurs prédites par le modèle et les valeurs réelles. C'est une erreur. L'un des objectifs d'un algorithme ML est d'avoir un faible biais.
La variance fait référence à la sensibilité du modèle aux petites fluctuations de l'ensemble de données d'apprentissage. Un autre objectif d'un algorithme ML est d'avoir une faible variance.
Pour un ensemble de données qui n'est pas exactement linéaire, il n'est pas possible d'avoir à la fois un biais et une variance faibles en même temps. Un modèle linéaire aura une faible variance mais un biais élevé, tandis qu'un polynôme de haut degré aura un faible biais mais une variance élevée.
Il est impossible d'échapper à la relation entre biais et variance dans l'apprentissage automatique.
- La diminution du biais augmente la variance.
- La diminution de la variance augmente le biais.
Donc, il y a un compromis entre les deux; le spécialiste ML doit décider, en fonction du problème assigné, du degré de biais et de variance pouvant être toléré. Sur cette base, le modèle final est construit.
25. Comment les courbes d'apprentissage peuvent-elles aider à créer un meilleur modèle ?
Les courbes d'apprentissage donnent l'indication de la présence d'un surajustement ou d'un sous-ajustement.
Dans une courbe d'apprentissage, l'erreur d'apprentissage et l'erreur de validation croisée sont tracées en fonction du nombre de points de données d'apprentissage. Une courbe d'apprentissage typique ressemble à ceci : 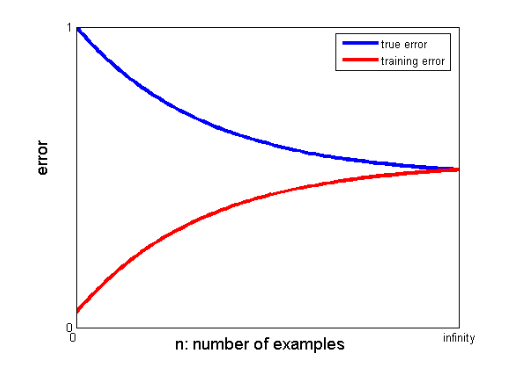
Si l'erreur d'apprentissage et l'erreur vraie (erreur de validation croisée) convergent vers la même valeur et que la valeur correspondante de l'erreur est élevée, cela indique que le modèle est sous-ajusté et souffre d'un biais élevé.
Entretiens d'apprentissage automatique et comment les réussir
Les entretiens d'apprentissage automatique peuvent varier selon les types ou les catégories, par exemple, quelques recruteurs posent de nombreuses questions d'entretien de régression linéaire . Lorsqu'ils optent pour le rôle d'entretien d'ingénieur en apprentissage machine, ils peuvent se spécialiser dans des catégories telles que le codage, la recherche, l'étude de cas, la gestion de projet, la présentation, la conception de système et les statistiques. Nous nous concentrerons sur les types de catégories les plus courants et sur la manière de s'y préparer.
- Codage
Le codage et la programmation sont des éléments importants d'un entretien d'apprentissage automatique et sont fréquemment utilisés pour sélectionner les candidats. Pour réussir ces entretiens, vous devez avoir de solides capacités de programmation. Les entretiens de codage durent généralement de 45 à 60 minutes et sont composés de seulement deux questions. L'intervieweur pose le sujet et s'attend à ce que le candidat l'aborde dans le moins de temps possible.
Comment se préparer - Vous pouvez vous préparer à ces entretiens en ayant une bonne compréhension des structures de données, des complexités du temps et de l'espace, des compétences en gestion et la capacité de comprendre et de résoudre un problème. upGrad propose un excellent cours de génie logiciel qui peut vous aider à améliorer vos compétences en codage et à réussir cet entretien.
2. Apprentissage automatique
Votre compréhension de l'apprentissage automatique sera évaluée au moyen d'entretiens. Les couches convolutives, les réseaux de neurones récurrents, les réseaux d'adversaires génératifs, la reconnaissance vocale et d'autres sujets peuvent être couverts en fonction des besoins de l'emploi.
Comment se préparer - Pour réussir cet entretien, vous devez vous assurer que vous avez une compréhension approfondie des rôles et des responsabilités du poste. Cela vous aidera à identifier les spécifications de ML que vous devez étudier. Cependant, si vous ne rencontrez aucune spécification, vous devez comprendre en profondeur les bases. Un cours approfondi en ML fourni par upGrad peut vous aider. Vous pouvez également étudier les derniers articles sur le ML et l'IA pour comprendre leurs dernières tendances et vous pouvez les intégrer régulièrement.
3. Dépistage
Cet entretien est quelque peu informel et constitue généralement l'un des points initiaux de l'entretien. Un employeur potentiel s'en occupe souvent. L'objectif principal de cet entretien est de fournir au candidat une idée de l'entreprise, du rôle et des fonctions. Dans une ambiance plus informelle, le candidat est également interrogé sur son passé afin de déterminer si son domaine d'intérêt correspond au poste.
Comment se préparer - Il s'agit d'une partie très non technique de l'entretien. Tout ce qui est requis est votre honnêteté et les bases de votre spécialisation en Machine Learning.
4. Conception du système
De tels entretiens testent la capacité d'une personne à créer une solution entièrement évolutive du début à la fin. La majorité des ingénieurs sont tellement préoccupés par un problème qu'ils négligent souvent le tableau d'ensemble. Un entretien de conception de système nécessite une compréhension de nombreux éléments qui se combinent pour produire une solution. Ces éléments incluent la disposition frontale, l'équilibreur de charge, le cache, etc. Un système de bout en bout efficace et évolutif est plus facile à développer lorsque ces problèmes sont bien compris.
Comment se préparer – Comprendre les concepts et les composants du projet de conception du système. Utilisez des exemples concrets pour expliquer la structure à votre intervieweur pour une meilleure compréhension du projet.
Blogs populaires sur l'apprentissage automatique et l'intelligence artificielle
| IdO : histoire, présent et avenir | Tutoriel d'apprentissage automatique : Apprendre le ML | Qu'est-ce que l'algorithme ? Simple et facile |
| Salaire d'ingénieur en robotique en Inde: tous les rôles | Une journée dans la vie d'un ingénieur en apprentissage automatique : que font-ils ? | Qu'est-ce que l'IoT (Internet des objets) |
| Permutation vs combinaison : Différence entre permutation et combinaison | Top 7 des tendances en matière d'intelligence artificielle et d'apprentissage automatique | Apprentissage automatique avec R : tout ce que vous devez savoir |

S'il existe un écart significatif entre les valeurs convergentes des erreurs d'apprentissage et de validation croisée, c'est-à-dire que l'erreur de validation croisée est nettement supérieure à l'erreur d'apprentissage, cela suggère que le modèle surajuste les données d'apprentissage et souffre d'une variance élevée. .
Ingénieurs en apprentissage automatique : mythes contre réalités
C'est la fin de la première section de cette série. Restez dans les parages pour la prochaine partie de la série qui consiste en des questions basées sur la régression logistique . N'hésitez pas à poster vos commentaires.
Co-écrit par - Ojas Agarwal
Vous pouvez consulter notre programme Executive PG en Machine Learning & AI , qui propose des ateliers pratiques, un mentor individuel de l'industrie, 12 études de cas et missions, le statut d'ancien IIIT-B, et plus encore.
Qu'entendez-vous par régularisation ?
La régularisation est une stratégie pour traiter le problème du surajustement du modèle. Le surajustement se produit lorsqu'un modèle compliqué est appliqué aux données d'apprentissage. Le modèle de base peut parfois ne pas être en mesure de généraliser les données, et le modèle compliqué peut surajuster les données. La régularisation est utilisée pour atténuer ce problème. La régularisation est le processus d'ajout de termes de coefficient (bêta) au problème de minimisation de telle sorte que les termes soient pénalisés et aient une ampleur modeste. Cela aide essentiellement à identifier les modèles de données tout en empêchant le surajustement en empêchant le modèle de devenir trop complexe.
Que comprenez-vous de l'ingénierie des fonctionnalités ?
Le processus de transformation des données d'origine en fonctionnalités qui décrivent mieux le problème sous-jacent aux modèles prédictifs, résultant en une précision améliorée du modèle sur des données invisibles, est connu sous le nom d'ingénierie des fonctionnalités. En termes simples, l'ingénierie des fonctionnalités fait référence à la création de fonctionnalités supplémentaires qui peuvent aider à mieux comprendre et modéliser un problème. Il existe deux types d'ingénierie de fonctionnalités : axée sur l'entreprise et axée sur les données. L'incorporation de fonctionnalités d'un point de vue commercial est au centre de l'ingénierie des fonctionnalités axée sur l'entreprise.
Quel est le compromis biais-variance ?
L'écart entre le modèle - les valeurs prédites et les valeurs réelles est appelé biais. C'est une erreur. Un faible biais est l'un des objectifs d'un algorithme ML. La vulnérabilité du modèle à de minuscules changements dans l'ensemble de données d'apprentissage est appelée variance. La faible variance est un autre objectif d'un algorithme ML. Il est impossible d'avoir à la fois un faible biais et une faible variance dans un ensemble de données qui n'est pas parfaitement linéaire. La variance d'un modèle linéaire est faible, mais le biais est important, tandis que la variance d'un polynôme de haut degré est faible, mais le biais est élevé. En machine learning, le lien entre biais et variation est incontournable.
