Introduction à la fonction de densité de probabilité [formule, propriétés, applications, exemples]

La fonction de densité de probabilité (PDF) est une expression statistique qui indique la distribution de probabilité d'une variable aléatoire discrète. La distribution de probabilité, en termes simples, peut être définie comme la probabilité d'un résultat d'une variable aléatoire comme une action ou un ETF. Les variables discrètes se produisent contrairement à une variable aléatoire continue dont la valeur précise peut être déterminée.

Par exemple, la valeur d'un scrip sur un marché boursier n'a que deux décimales (par exemple, 65,76) dans une variable aléatoire discrète au lieu d'une variable continue avec n'importe quel nombre de décimales (exemple : 65,7685434567).

Une fonction de densité de probabilité est un outil statistique utilisé pour déterminer la probabilité du résultat d'une variable aléatoire discrète. Lorsqu'ils sont tracés sur un graphique, les PDF ressemblent à une courbe en cloche dans laquelle l'aire sous la courbe représente la probabilité du résultat.

Lorsqu'elle est projetée sous forme de modèle graphique, l'aire sous la courbe représente la plage dans laquelle les valeurs des variables aléatoires discrètes tomberont. Ainsi, l'aire totale sous la courbe est égale à la probabilité du résultat de la variable.

La fonction de densité de probabilité peut déterminer la probabilité qu'une variable aléatoire tombe dans une plage de valeurs spécifique.

En règle générale, les fonctions de densité de probabilité analysent les risques et les revenus potentiels associés à un fonds spécifique sur le marché boursier.

Conditions à satisfaire par une fonction pour être considérée comme une fonction de densité de probabilité

La valeur d'une variable discrète peut être mesurée avec précision contrairement à une variable continue qui peut avoir un nombre infini de valeurs. Toute fonction doit satisfaire aux deux conditions ci-dessous pour être une fonction de densité de probabilité :

• La valeur f(x) pour chaque valeur possible de la variable aléatoire doit être positive (non négative).
• La valeur intégrale de l'aire totale de la courbe (intégrale de toutes les valeurs possibles de la variable aléatoire) doit être 1.

Différence entre la fonction de densité de probabilité et la fonction de distribution de probabilité

Les variables aléatoires peuvent avoir plusieurs valeurs. La description de chaque valeur possible qu'une variable aléatoire peut avoir s'appelle sa distribution de probabilité.

La distribution de probabilité donne un ensemble de résultats et leurs probabilités associées. La fonction statistique qui représente une distribution de probabilité continue est connue sous le nom de fonction de densité de probabilité.

Il existe un autre outil statistique qui représente une distribution de probabilité discrète appelée la fonction de masse de probabilité. Cela donne un compte rendu détaillé de tous les résultats possibles et de leurs probabilités de probabilité.

Expression des fonctions de densité de probabilité

Si la variable aléatoire est discrète, sa distribution de probabilité est appelée fonction de masse de probabilité, et s'il s'agit d'une variable continue, la distribution de probabilité est appelée fonction de densité de probabilité.

Un PDF est utilisé lorsque la variable aléatoire en question a une plage de valeurs possibles. Leur distribution de probabilité est utilisée pour déterminer la valeur exacte.

Soit la variable aléatoire désignée par X. La fonction de densité de probabilité, f de la variable aléatoire X peut être exprimée comme

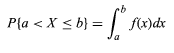
• La valeur de la variable aléatoire est comprise entre a et b.
• Si X désigne la probabilité de sélectionner un nombre particulier dans la plage (intervalle) r et s , alors la fonction de densité de probabilité peut être exprimée comme

f ( x ) = 1/( s − r ) pour r < x < s et f ( x ) = 0 pour x < r ou x > s .

• Le PDF F est représenté par :

F ( X ) = P { X ≤ X }

qui s'appelle la fonction de distribution ou la fonction de distribution cumulative de X.

Considérant que la variable aléatoire X a une fonction de distribution de probabilité f ( x ), alors la relation entre f et F peut être établie comme

F ′(. X ) = F ( X )

La fonction de distribution d'une variable aléatoire discrète est différente de sa fonction de distribution de probabilité. La relation entre les deux peut être exprimée comme suit :

L'espérance de la variable aléatoire est notée,

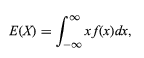
Ainsi, toutes les variables discrètes et aléatoires peuvent être traitées uniformément à l'aide d'une théorie combinée.

La formule de la fonction de densité de probabilité

La probabilité d'une variable aléatoire continue X sur une valeur fixe x est toujours 0. Dans ce cas, P(X = x) ne peut pas être utilisé. La valeur de X comprise entre une plage de valeurs (a,b) doit être déterminée. Pour déterminer la même chose, la formule suivante est utilisée.

Propriétés d'une fonction de densité de probabilité

Une variable aléatoire continue qui prend sa valeur entre la plage (a,b), par exemple, sera estimée en calculant l'aire sous la courbe et l'axe X tracé avec (a) comme limite inférieure et (b) comme sa limite supérieure. La fonction de densité de probabilité pour ce qui précède est représentée par :

La fonction de densité de probabilité est positive (non négative) pour toutes les valeurs possibles. Cela signifie f(x)≥ 0, pour tout x. La zone située entre la courbe de densité et l'axe X (axe horizontal) est égale à 1.

Cela peut également être noté comme suit :

La courbe de la fonction de densité est continue sur toute la plage donnée, qui est clairement définie par rapport à une série de valeurs continues ou au domaine de la variable.

Rejoignez le cours d'apprentissage automatique en ligne des meilleures universités du monde - Masters, programmes de troisième cycle pour cadres et programme de certificat avancé en ML et IA pour accélérer votre carrière.

Applications de la fonction de densité de probabilité

• La fonction de densité de probabilité est utilisée dans la modélisation annuelle des niveaux de concentration atmosphérique de NO.
• Modélisation de la combustion des moteurs diesel.
• En statistique, la fonction de densité de probabilité est utilisée pour déterminer les possibilités de résultat d'une variable aléatoire.

Exemples de fonction de densité de probabilité

• Exemple 1

Vous trouverez ci-dessous un exemple de la façon dont la fonction de densité de probabilité (PDF) est utilisée pour déterminer le potentiel de risque d'un investisseur en bourse :

Premièrement, les PDF sont générés comme un outil graphique basé sur des informations historiques.

La forme la plus courante de PDF est la projection neutre, où le risque est égal à la récompense dans une gamme de possibilités. Les investisseurs ayant moins de capacité de prise de risque ne seront récompensés que par des bénéfices limités et se situent donc sous le côté gauche de la courbe en cloche. À l'inverse, les investisseurs ayant une capacité de prise de risque élevée sont susceptibles d'être récompensés par des rendements plus élevés et, par conséquent, de se situer sous le côté droit de la courbe.

La plupart des investisseurs relèvent d'une capacité de prise de risque moyenne et occupent donc le milieu de la courbe.

Cela aide à analyser la catégorie d'investisseurs sur la base des données reçues. Cela aide les courtiers en bourse à identifier leur catégorie cible de clients pour vendre leurs produits.

• Exemple 2

L'une des applications essentielles de la fonction de densité de probabilité est la variable aléatoire gaussienne, également appelée variable aléatoire normale.

Dans les deux cas, le graphique donne une courbe en cloche pour la fonction de densité de probabilité.

La densité peut être exprimée comme

Le graphique de l'équation de densité ci-dessus est donné ci-dessous.

La zone sous la courbe représente la valeur réelle de la variable aléatoire gaussienne.

Conclusion

La fonction de densité de probabilité joue un rôle essentiel dans l'apprentissage automatique. Pour les étudiants qui envisagent une carrière dans l'apprentissage automatique et l'intelligence artificielle, nous recommandons fortement de s'inscrire au programme de certificat avancé IIT d'upGrad en apprentissage automatique . Le programme est personnalisé et conçu pour permettre aux professionnels expérimentés de déployer des modèles d'apprentissage automatique à l'aide de la technologie du cloud computing.

Le programme est conçu par des professeurs de l'IIT Madras et des experts de l'industrie pour rendre le processus d'apprentissage plus pertinent et pratique. Le programme offre une certification mondialement reconnue du collège d'ingénieurs convoité et classé n ° 1 en Inde et un support de placement à 360 degrés d'upGrad.

De plus, vous avez de nombreuses opportunités de collaborer sur des projets à grande échelle avec la base d'apprenants rémunérés d'upGrad de plus de 40 000.

Rendez-vous sur notre site Web pour commencer votre parcours d'apprentissage!