Introduction à la régression multivariée dans l'apprentissage automatique : guide complet

Ce n'est un secret pour personne que la technologie d'aujourd'hui est axée sur les données. Les données peuvent n'être qu'une compilation de chiffres, mais elles peuvent être traitées de manière significative pour extraire la productivité et l'ingéniosité des entreprises afin de rester compétitives et durables à long terme. En l'occurrence, l'analyse des données est la réponse pour obtenir des estimations précises à partir d'informations brutes.

L'analyse des données est une technique qui implique des idées statistiques et logiques pour examiner, traiter et transformer les données en une forme utilisable. Les solutions tirées de l'analyse des données sont utilisées dans les entreprises pour prendre des décisions vitales. La science des données ainsi que l'analyse des données sont utilisées pour prédire les résultats futurs avec une grande précision. Il s'agit d'un processus d'utilisation de techniques scientifiques et d'algorithmes pour obtenir des informations viables à partir d'un pool de données.

Un problème courant auquel sont confrontés les professionnels des données est la manière de déterminer s'il existe une relation statistique entre une variable de réponse (notée Y) et des variables explicatives (notées Xi).

La réponse à cette préoccupation est l'analyse de régression. Comprenons cela plus en détail.

Qu'est-ce que l'analyse de régression ?

L'analyse de régression est l'une des méthodes populaires d'analyse de données qui suit un algorithme d'apprentissage automatique contrôlé ou supervisé. C'est une technique efficace pour identifier et établir une relation entre les variables dans les données.

L'analyse de régression consiste à trier des variables viables à l'aide de stratégies mathématiques pour tirer des conclusions très précises sur ces variables triées.

Qu'est-ce que la régression multivariée ?

Multivariate est un algorithme d'apprentissage automatique contrôlé ou supervisé qui analyse plusieurs variables de données. C'est une continuation de la régression multiple qui implique une variable dépendante et de nombreuses variables indépendantes. La sortie est prédite en fonction du nombre de variables indépendantes.

La régression multivariée trouve une formule qui explique la réponse simultanée des facteurs présents dans les variables aux changements dans les autres. Ils sont utilisés pour étudier les données dans divers domaines. Par exemple, dans l'immobilier, la régression multivariée est utilisée pour prédire le prix d'une maison en fonction de plusieurs facteurs tels que son emplacement, le nombre de pièces et les commodités disponibles.

Fonction de coût dans la régression multivariée

La fonction de coût alloue un coût aux échantillons lorsque le résultat d'un modèle s'écarte des données observées. L'équation de la fonction de coût est le total du carré de la différence entre la valeur prédite et la valeur réelle divisé par deux fois la longueur de l'ensemble de données.

Voici un exemple :

Résultat :

La source

Comment utiliser l'analyse de régression multivariée ?

Les processus impliqués dans l'analyse de régression multivariée comprennent la sélection des caractéristiques, l'ingénierie des caractéristiques, la normalisation des caractéristiques, les fonctions de perte de sélection, l'analyse des hypothèses et la création d'un modèle de régression.

1. Sélection des caractéristiques : c'est l'étape la plus importante de la régression multivariée. Également connu sous le nom de sélection de variables, ce processus consiste à sélectionner des variables viables pour construire des modèles efficaces.
2. Normalisation des fonctionnalités : cela implique la mise à l'échelle des fonctionnalités pour maintenir une distribution et des ratios de données rationalisés. Cela aide à une meilleure analyse des données. La valeur de toutes les fonctionnalités peut être modifiée en fonction des besoins.
3. Sélection de la fonction de perte et de l'hypothèse : La fonction de perte est utilisée pour prédire les erreurs. La fonction de perte entre en jeu lorsque la prédiction de l'hypothèse change par rapport aux chiffres réels. Ici, l'hypothèse représente la valeur prédite à partir de la caractéristique ou de la variable.
4. Paramètre d' hypothèse de fixation : le paramètre de l'hypothèse est fixe ou défini de manière à minimiser la fonction de perte et à améliorer la prédiction.
5. Réduction de la fonction de perte : La fonction de perte est minimisée en générant un algorithme spécifiquement pour la minimisation des pertes sur l'ensemble de données qui à son tour facilite la modification des paramètres d'hypothèse. La descente de gradient est l'algorithme le plus couramment utilisé pour la minimisation des pertes. L'algorithme peut également être utilisé pour d'autres actions une fois la minimisation des pertes terminée.
6. Analyse de la fonction d'hypothèse : La fonction de l'hypothèse doit être analysée car elle est cruciale pour prédire les valeurs. Une fois la fonction analysée, elle est ensuite testée sur des données de test.

Voyons maintenant les deux façons d'utiliser la régression multivariée.

1. Régression linéaire multivariée

La régression linéaire multivariée ressemble à la régression linéaire simple, sauf que dans la régression linéaire multivariée, plusieurs variables indépendantes contribuent aux variables dépendantes et donc plusieurs coefficients sont utilisés dans le calcul.

• Il est utilisé pour dériver une relation mathématique entre plusieurs variables aléatoires. Il explique combien de variables indépendantes multiples sont associées à une variable dépendante.
• Les détails des multiples variables indépendantes sont utilisés pour faire une prédiction précise de l'influence qu'elles ont sur la variable de résultat.
• Le modèle de régression linéaire multivariée génère une relation sous une forme linéaire (une forme de ligne droite) avec la meilleure approximation de chaque point de données.
• L'équation du modèle de régression linéaire multivariée est :

yi​=β0​+β1​xi1​+β2​xi2​+…+βp​xip​+

où pour i=n observations :

La source

Quand peut-on utiliser la régression linéaire ?

Le modèle de régression linéaire ne peut être utilisé que lorsqu'il existe deux variables continues dont l'une est dépendante et l'autre est indépendante.

La variable indépendante est utilisée comme paramètre pour déterminer la valeur ou le résultat de la variable dépendante.

2. Régression logistique multivariée

La régression logistique est un algorithme utilisé pour prédire un résultat binaire basé sur plusieurs variables indépendantes. Un résultat binaire a deux possibilités, soit le scénario se produit (représenté par 1) ou il ne se produit pas (désigné par 0).

La régression logistique est utilisée lorsque l'on travaille sur des données binaires, les données où le résultat (ou la variable dépendante) est dichotomique.

Où peut-on utiliser la régression logistique ?

La régression logistique est principalement utilisée pour traiter les problèmes de classification. Par exemple, pour déterminer si un e-mail est un spam ou non et si une transaction particulière est malveillante ou non. Dans l'analyse des données, il est utilisé pour prendre des décisions calculées afin de minimiser les pertes et d'augmenter les profits.

La régression logistique multivariée est utilisée lorsqu'il y a une variable dépendante et plusieurs résultats. Elle diffère de la régression logistique en ayant plus de deux résultats possibles.

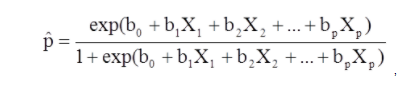
X1 à Xp sont des variables indépendantes distinctes.

b0 à bp sont les coefficients de régression

Le modèle de régression logistique multiple peut également être écrit sous une forme différente. Dans le formulaire ci-dessous, le résultat est le logarithme attendu des chances que le résultat soit présent,

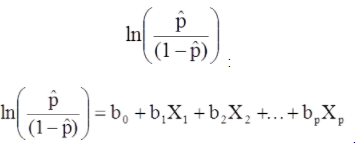
Le modèle de régression logistique multiple peut également être écrit sous une forme différente. Dans le formulaire ci-dessous, le résultat est le logarithme attendu de la probabilité que le résultat soit présent.

Le côté droit de l'équation ci-dessus ressemble à l'équation de régression linéaire, mais la méthode de recherche des coefficients de régression diffère.

Hypothèses du modèle de régression multivariée

• Les variables dépendantes et indépendantes ont une relation linéaire.
• Les variables indépendantes n'ont pas de forte corrélation entre elles.
• Les observations de yi​ sont choisies aléatoirement et individuellement dans la population.

Hypothèses dans le modèle de régression logistique multivariée

• La variable dépendante est nominale ou ordinale. Les variables nominales ont deux ou plusieurs catégories sans aucune organisation significative. Les variables ordinales peuvent également avoir deux catégories ou plus, mais elles ont une structure et peuvent être classées.
• Il peut y avoir une ou plusieurs variables indépendantes qui peuvent être ordinales, continues ou nominales. Les variables continues sont celles qui peuvent avoir des valeurs infinies dans une plage spécifique.
• Les variables dépendantes sont mutuellement exclusives et exhaustives.
• Les variables indépendantes n'ont pas de forte corrélation entre elles.

Avantages de la régression multivariée

1. La régression multivariée nous aide à étudier les relations entre plusieurs variables dans l'ensemble de données.
2. La corrélation entre les variables dépendantes et indépendantes aide à prédire le résultat.
3. C'est l'un des algorithmes les plus pratiques et les plus populaires utilisés dans l'apprentissage automatique.

Inconvénients de la régression multivariée

• La complexité des techniques multivariées nécessite des calculs mathématiques complexes.
• Il n'est pas facile d'interpréter la sortie du modèle de régression multivariée car il y a des incohérences dans les sorties de perte et d'erreur.
• Les modèles de régression multivariés ne peuvent pas être appliqués à des ensembles de données plus petits ; ils sont conçus pour produire des résultats précis lorsqu'il s'agit d'ensembles de données plus volumineux.

Si vous souhaitez en savoir plus sur la régression multivariée et d'autres sujets complexes de la science des données, upGrad a la solution qu'il vous faut. Notre cours de maîtrise ès sciences en science des données de 18 mois de l' Université John Moores de Liverpool couvre plus de 500 heures d'apprentissage rigoureuses, 25 sessions de coaching (organisées sur une base 1: 8) et plus de 20 sessions en direct. upGrad propose également une assistance pédagogique 1:1 et un accompagnement à l'orientation professionnelle à 360° pour que les étudiants transforment leur carrière. Les apprenants peuvent tirer parti de l'apprentissage entre pairs sur la plate-forme mondiale avec plus de 40 000 apprenants rémunérés et travailler sur des projets collaboratifs dans six spécialisations fonctionnelles pour maximiser leur expérience d'apprentissage.