Implémenter l'algorithme de tri de comptage en Java

Publié: 2023-01-30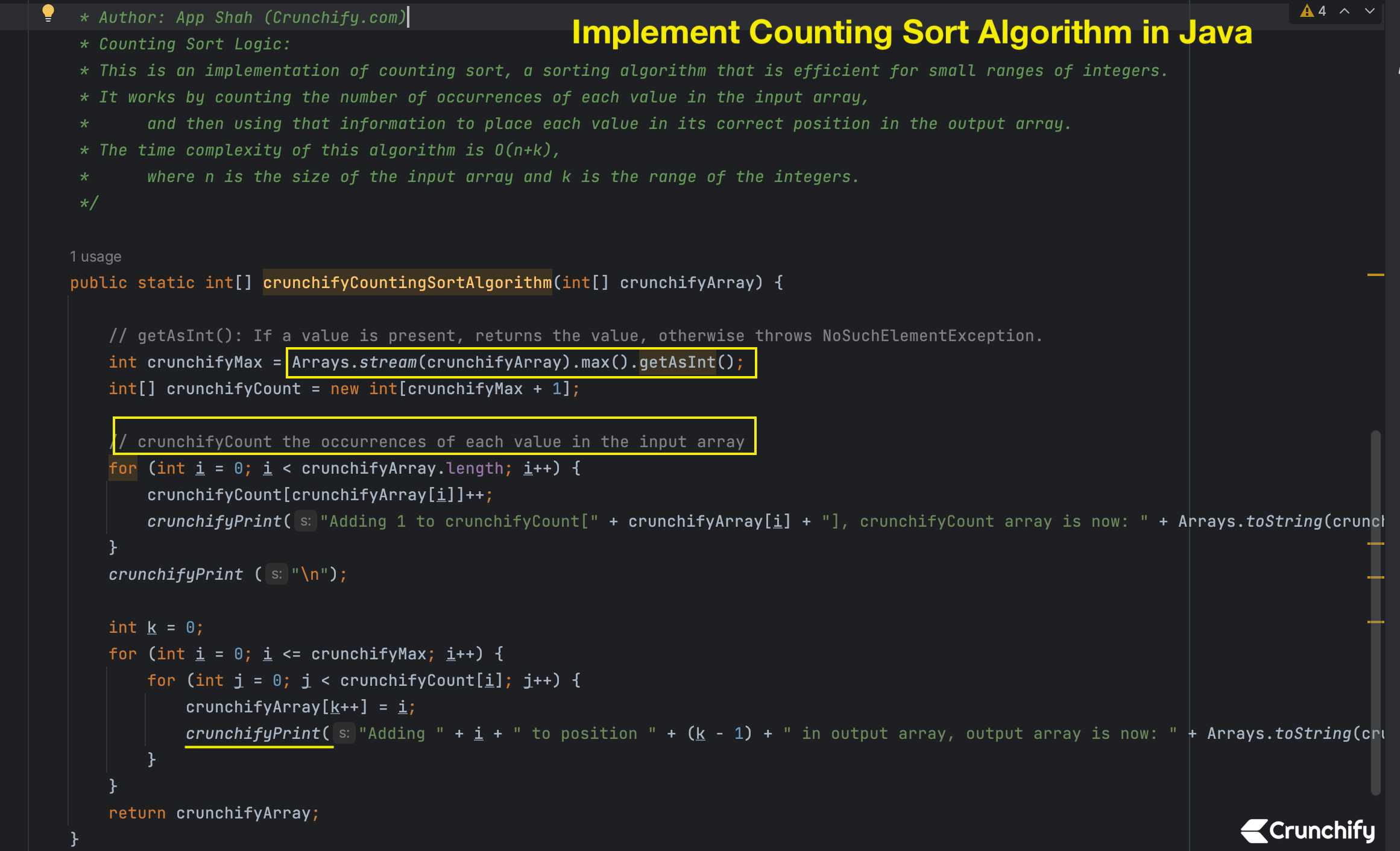

Qu'est-ce que l'algorithme de tri par comptage ?

Tri par comptage, un algorithme de tri efficace pour les small ranges of integers . Cela fonctionne en comptant le nombre d'occurrences de chaque valeur dans le tableau d'entrée, puis en utilisant ces informations pour placer chaque valeur à sa position correcte dans le tableau de sortie.

La complexité temporelle de cet algorithme est O(n+k) , où n est la taille du tableau d'entrée et k est la plage des entiers.

CrunchifyCountingSortAlgo.java

Voici une implémentation complète de Counting Sort en Java. Copiez-le simplement dans votre IDÉE préférée et exécutez-le.

 package crunchify.com.java.tutorials ;

importer java.util.Arrays ;

/**
 * @author Crunchify.com
 * Programme : Comment implémenter l'algorithme de tri par comptage en java ?
 * Le tri par comptage est un algorithme de tri qui trie les éléments d'un tableau 
 * en comptant le nombre d'occurrences de chaque élément unique du tableau.
 */

classe publique CrunchifyCountingSortAlgo {

    public static void main(String[] args) {

        // Tableau d'entiers de 10 éléments
        int[] crunchifyArray = {9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3} ;

        crunchifyPrint("Original Array : " + Arrays.toString(crunchifyArray));
        crunchifyPrint ("\n");

        CrunchifyCountingSortAlgo crunchify = new CrunchifyCountingSortAlgo();
        crunchify.crunchifyCountingSortAlgorithm(crunchifyArray);

        crunchifyPrint ("\n");
        crunchifyPrint("Résultat de l'algorithme de tri par comptage Crunchify : " + Arrays.toString(crunchifyArray));
    }

    vide statique privé crunchifyPrint(String s) {

        System.out.println(s);
    }


    /**
     * Auteur : App Shah (Crunchify.com)
     *
     * Comptage de la logique de tri :
     * Il s'agit d'une implémentation du tri par comptage, un algorithme de tri efficace pour les petites plages d'entiers.
     * Cela fonctionne en comptant le nombre d'occurrences de chaque valeur dans le tableau d'entrée,
     * puis en utilisant ces informations pour placer chaque valeur dans sa position correcte dans le tableau de sortie.
     * La complexité temporelle de cet algorithme est O(n+k),
     * où n est la taille du tableau d'entrée et k est la plage des nombres entiers.
     */


    public static int[] crunchifyCountingSortAlgorithm(int[] crunchifyArray) {

        // getAsInt() : si une valeur est présente, renvoie la valeur, sinon lève NoSuchElementException.
        int crunchifyMax = Arrays.stream(crunchifyArray).max().getAsInt();
        int[] crunchifyCount = new int[crunchifyMax + 1] ;

        // crunchifyCompte les occurrences de chaque valeur dans le tableau d'entrée
        for (int je = 0; je < crunchifyArray.length; je++) {
            crunchifyCount[crunchifyArray[i]]++ ;
            crunchifyPrint("Ajout de 1 à crunchifyCount[" + crunchifyArray[i] 
                    + "], le tableau crunchifyCount est maintenant : " + Arrays.toString(crunchifyCount));
        }

        crunchifyPrint ("\n");

        entier k = 0 ;
        pour (int je = 0; je <= crunchifyMax; je++) {
            for (int j = 0; j < crunchifyCount[i]; j++) {
                crunchifyArray[k++] = je ;
                crunchifyPrint("Ajout de " + i + " à la position " + (k - 1) 
                        + " dans le tableau de sortie, le tableau de sortie est maintenant : " + Arrays.toString(crunchifyArray));
            }
        }

        return crunchifyArray ;
    }

}

Exécutez simplement le programme ci-dessus en tant qu'application Java dans IntelliJ IDEA ou Eclipse IDE et vous obtiendrez le résultat ci-dessous.

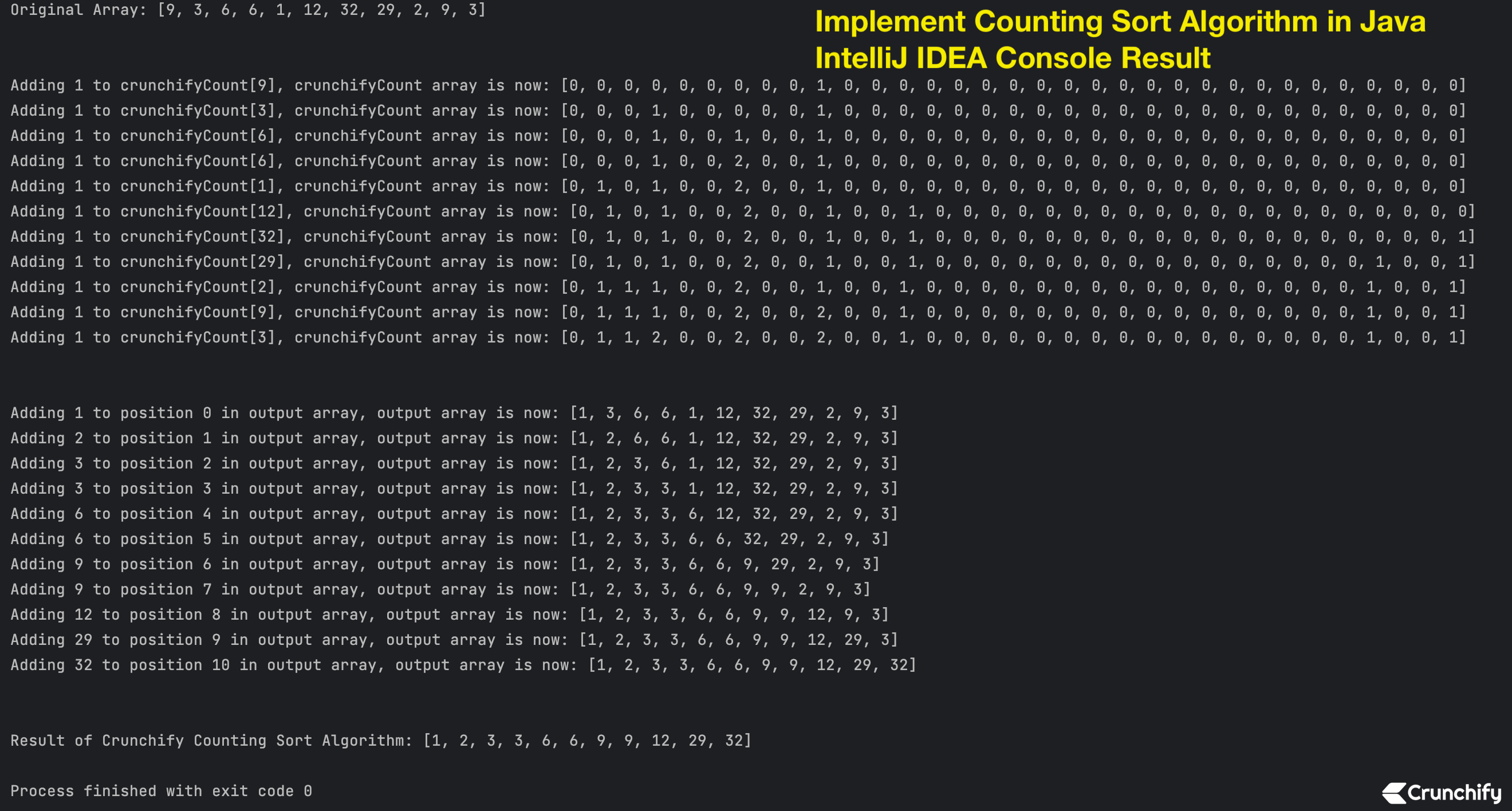
Résultat de la console IntelliJ IDEA

 Tableau d'origine : [9, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3]


En ajoutant 1 à crunchifyCount[9], le tableau crunchifyCount est maintenant : [0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
En ajoutant 1 à crunchifyCount[3], le tableau crunchifyCount est maintenant : [0, 0, 0, 1, 0, 0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
En ajoutant 1 à crunchifyCount[6], le tableau crunchifyCount est maintenant : [0, 0, 0, 1, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
En ajoutant 1 à crunchifyCount[6], le tableau crunchifyCount est maintenant : [0, 0, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
En ajoutant 1 à crunchifyCount[1], le tableau crunchifyCount est maintenant : [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
En ajoutant 1 à crunchifyCount[12], le tableau crunchifyCount est maintenant : [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0]
En ajoutant 1 à crunchifyCount[32], le tableau crunchifyCount est maintenant : [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1]
En ajoutant 1 à crunchifyCount[29], le tableau crunchifyCount est maintenant : [0, 1, 0, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
En ajoutant 1 à crunchifyCount[2], le tableau crunchifyCount est maintenant : [0, 1, 1, 1, 0, 0, 2, 0, 0, 1, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
En ajoutant 1 à crunchifyCount[9], le tableau crunchifyCount est maintenant : [0, 1, 1, 1, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]
En ajoutant 1 à crunchifyCount[3], le tableau crunchifyCount est maintenant : [0, 1, 1, 2, 0, 0, 2, 0, 0, 2, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 1]


En ajoutant 1 à la position 0 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 3, 6, 6, 1, 12, 32, 29, 2, 9, 3]
En ajoutant 2 à la position 1 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 6, 6, 1, 12, 32, 29, 2, 9, 3]
En ajoutant 3 à la position 2 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 6, 1, 12, 32, 29, 2, 9, 3]
En ajoutant 3 à la position 3 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 1, 12, 32, 29, 2, 9, 3]
En ajoutant 6 à la position 4 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 12, 32, 29, 2, 9, 3]
En ajoutant 6 à la position 5 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 6, 32, 29, 2, 9, 3]
En ajoutant 9 à la position 6 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 6, 9, 29, 2, 9, 3]
En ajoutant 9 à la position 7 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 6, 9, 9, 2, 9, 3]
En ajoutant 12 à la position 8 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 6, 9, 9, 12, 9, 3]
En ajoutant 29 à la position 9 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 3]
En ajoutant 32 à la position 10 dans le tableau de sortie, le tableau de sortie est maintenant : [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32]


Résultat de l'algorithme de tri de comptage Crunchify : [1, 2, 3, 3, 6, 6, 9, 9, 12, 29, 32]

Processus terminé avec le code de sortie 0

Implémenter l'algorithme de tri de comptage en Java - Résultat IntelliJ IDEA

Faites-moi savoir si vous rencontrez un problème d'exécution au-dessus du programme Java Counting Sort Algorithm.