Bayes naïf gaussien : ce que vous devez savoir ?
Publié: 2021-02-22Table des matières
Bayes naïf gaussien
Naive Bayes est un algorithme d'apprentissage automatique probabiliste utilisé pour de nombreuses fonctions de classification et est basé sur le théorème de Bayes. Gaussian Naive Bayes est l'extension de naive Bayes. Alors que d'autres fonctions sont utilisées pour estimer la distribution des données, la distribution gaussienne ou normale est la plus simple à mettre en œuvre car vous devrez calculer la moyenne et l'écart type des données d'apprentissage.
Qu'est-ce que l'algorithme naïf de Bayes ?
Naive Bayes est un algorithme d'apprentissage automatique probabiliste qui peut être utilisé dans plusieurs tâches de classification. Les applications typiques de Naive Bayes sont la classification des documents, le filtrage du spam, la prédiction, etc. Cet algorithme est basé sur les découvertes de Thomas Bayes et d'où son nom.
Le nom "Naïf" est utilisé car l'algorithme intègre dans son modèle des fonctionnalités indépendantes les unes des autres. Toute modification de la valeur d'une caractéristique n'a pas d'impact direct sur la valeur de toute autre caractéristique de l'algorithme. Le principal avantage de l'algorithme Naive Bayes est qu'il s'agit d'un algorithme simple mais puissant.
Il est basé sur le modèle probabiliste où l'algorithme peut être codé facilement et les prédictions se font rapidement en temps réel. Par conséquent, cet algorithme est le choix typique pour résoudre les problèmes du monde réel car il peut être réglé pour répondre instantanément aux demandes des utilisateurs. Mais avant de plonger profondément dans Naive Bayes et Gaussian Naive Bayes, nous devons savoir ce que l'on entend par probabilité conditionnelle.
La probabilité conditionnelle expliquée
Nous pouvons mieux comprendre la probabilité conditionnelle avec un exemple. Lorsque vous lancez une pièce de monnaie, la probabilité d'avoir une avance ou une pile est de 50 %. De même, la probabilité d'obtenir un 4 lorsque vous lancez des dés avec des visages est de 1/6 ou 0,16.
Si nous prenons un paquet de cartes, quelle est la probabilité d'obtenir une dame à condition qu'il s'agisse d'un pique ? Puisque la condition est déjà définie qu'il doit s'agir d'un pique, le dénominateur ou l'ensemble de sélection devient 13. Il n'y a qu'une seule reine dans les piques, donc la probabilité de choisir une reine de pique devient 1/13 = 0,07.

La probabilité conditionnelle de l'événement A étant donné l'événement B signifie la probabilité que l'événement A se produise étant donné que l'événement B s'est déjà produit. Mathématiquement, la probabilité conditionnelle de A étant donné B peut être notée P[A|B] = P[A ET B] / P[B].
Prenons un petit exemple complexe. Prenez une école avec un total de 100 élèves. Cette population peut être délimitée en 4 catégories : étudiants, enseignants, hommes et femmes. Considérez le tableau ci-dessous :
| Femme | Homme | Total | |
| Prof | 8 | 12 | 20 |
| Élève | 32 | 48 | 80 |
| Total | 40 | 50 | 100 |
Ici, quelle est la probabilité conditionnelle qu'un certain résident de l'école soit un enseignant étant donné la condition qu'il soit un homme.
Pour calculer cela, vous devrez filtrer la sous-population de 60 hommes et descendre jusqu'aux 12 enseignants masculins.
Ainsi, la probabilité conditionnelle attendue P[Enseignant | Homme] = 12/60 = 0,2
P (Enseignant | Homme) = P (Enseignant ∩ Homme) / P(Homme) = 12/60 = 0,2
Cela peut être représenté par un enseignant (A) et un homme (B) divisé par un homme (B). De même, la probabilité conditionnelle de B compte tenu de A peut également être calculée. La règle que nous utilisons pour Naive Bayes peut être déduite des notations suivantes :
P (A | B) = P (A ∩ B) / P(B)
P (B | UNE) = P (A ∩ B) / P(A)
La règle de Bayes
Dans la règle de Bayes, nous partons de P (X | Y) qui peut être trouvé à partir de l'ensemble de données d'apprentissage pour trouver P (Y | X). Pour ce faire, il vous suffit de remplacer A et B par X et Y dans les formules ci-dessus. Pour les observations, X serait la variable connue et Y serait la variable inconnue. Pour chaque ligne du jeu de données, vous devez calculer la probabilité de Y étant donné que X s'est déjà produit.
Mais que se passe-t-il lorsqu'il y a plus de 2 catégories dans Y ? Nous devons calculer la probabilité de chaque classe Y pour trouver celle qui est gagnante.
Par la règle de Bayes, on part de P (X | Y) pour trouver P (Y | X)
Connu à partir des données d'entraînement : P (X | Y) = P (X ∩ Y) / P(Y)
P (Preuve | Résultat)
Inconnu – à prédire pour les données de test : P (Y | X) = P (X ∩ Y) / P(X)
P (Résultat | Preuve)
Règle de Bayes = P (Y | X) = P (X | Y) * P (Y) / P (X)

Les Bayes naïfs
La règle de Bayes fournit la formule de la probabilité de Y étant donné la condition X. Mais dans le monde réel, il peut y avoir plusieurs variables X. Lorsque vous avez des fonctionnalités indépendantes, la règle de Bayes peut être étendue à la règle Naive Bayes. Les X sont indépendants les uns des autres. La formule Naive Bayes est plus puissante que la formule Bayes
Bayes naïf gaussien
Jusqu'ici, nous avons vu que les X sont dans des catégories mais comment calculer des probabilités quand X est une variable continue ? Si nous supposons que X suit une distribution particulière, vous pouvez utiliser la fonction de densité de probabilité de cette distribution pour calculer la probabilité des vraisemblances.
Si nous supposons que les X suivent une distribution gaussienne ou normale, nous devons substituer la densité de probabilité de la distribution normale et la nommer Gaussian Naive Bayes. Pour calculer cette formule, vous avez besoin de la moyenne et de la variance de X.
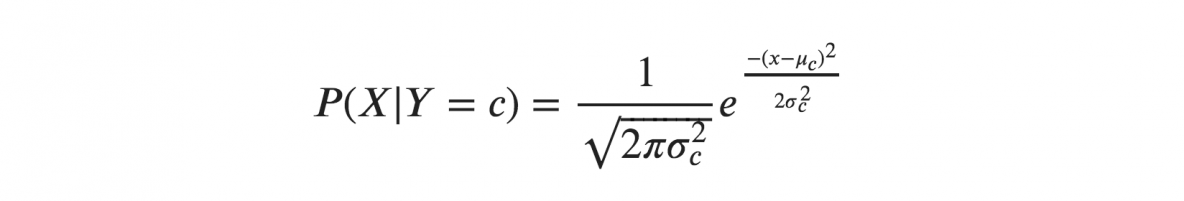
Dans les formules ci-dessus, sigma et mu sont la variance et la moyenne de la variable continue X calculées pour une classe c donnée de Y.
Représentation pour Gaussian Naive Bayes
La formule ci-dessus a calculé les probabilités des valeurs d'entrée pour chaque classe à travers une fréquence. Nous pouvons calculer la moyenne et l'écart type des x pour chaque classe pour l'ensemble de la distribution.
Cela signifie qu'en plus des probabilités pour chaque classe, nous devons également stocker la moyenne et l'écart type pour chaque variable d'entrée de la classe.
moyenne(x) = 1/n * somme(x)
où n représente le nombre d'instances et x est la valeur de la variable d'entrée dans les données.
écart type(x) = sqrt(1/n * sum(xi-mean(x)^2 ))
Ici, la racine carrée de la moyenne des différences de chaque x et la moyenne de x est calculée où n est le nombre d'instances, sum() est la fonction somme, sqrt() est la fonction racine carrée et xi est une valeur x spécifique .

Prédictions avec le modèle Gaussian Naive Bayes
La fonction de densité de probabilité gaussienne peut être utilisée pour faire des prédictions en remplaçant les paramètres par la nouvelle valeur d'entrée de la variable et, par conséquent, la fonction gaussienne donnera une estimation de la probabilité de la nouvelle valeur d'entrée.
Classificateur naïf de Bayes
Le classificateur Naive Bayes suppose que la valeur d'une caractéristique est indépendante de la valeur de toute autre caractéristique. Les classificateurs Naive Bayes ont besoin de données d'entraînement pour estimer les paramètres requis pour la classification. En raison de leur conception et de leur application simples, les classificateurs Naive Bayes peuvent convenir à de nombreux scénarios réels.
Conclusion
Le classificateur Gaussian Naive Bayes est une technique de classification rapide et simple qui fonctionne très bien sans trop d'effort et avec un bon niveau de précision.
Si vous souhaitez en savoir plus sur l'IA, l'apprentissage automatique, consultez le diplôme PG en apprentissage automatique et IA de IIIT-B & upGrad, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 études de cas et missions, Statut d'ancien de l'IIIT-B, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.
Apprenez le cours ML des meilleures universités du monde. Gagnez des programmes de maîtrise, Executive PGP ou Advanced Certificate pour accélérer votre carrière.
Qu'est-ce qu'un algorithme de Bayes naïf ?
Naive bayes est un algorithme d'apprentissage automatique classique. Ayant son origine dans les statistiques, naïve bayes est un algorithme simple et puissant. Naive bayes est une famille de classificateurs basés sur l'application d'une analyse de probabilité conditionnelle. Dans cette analyse, la probabilité conditionnelle d'un événement est calculée en utilisant la probabilité de chacun des événements individuels constituant l'événement. Les classificateurs Bayes naïfs se révèlent souvent extrêmement efficaces dans la pratique, en particulier lorsque le nombre de dimensions de l'ensemble de fonctionnalités est important.
Quelles sont les applications de l'algorithme de bayes naïf ?
Naive Bayes est utilisé dans la classification de texte, la classification de documents et l'indexation de documents. Dans les baies naïves, chaque caractéristique possible n'a pas de poids attribué dans la phase de prétraitement et les poids sont ensuite attribués pendant la formation ainsi que les phases de reconnaissance. L'hypothèse de base de l'algorithme de bayes naïf est que les caractéristiques sont indépendantes.
Qu'est-ce que l'algorithme Gaussian Naive Bayes ?
Gaussian Naive Bayes est un algorithme de classification probabiliste basé sur l'application du théorème de Bayes avec des hypothèses d'indépendance fortes. Dans le contexte de la classification, l'indépendance fait référence à l'idée que la présence d'une valeur d'une caractéristique n'influence pas la présence d'une autre (contrairement à l'indépendance dans la théorie des probabilités). Naïf fait référence à l'utilisation d'une hypothèse selon laquelle les caractéristiques d'un objet sont indépendantes les unes des autres. Dans le contexte de l'apprentissage automatique, les classificateurs Bayes naïfs sont connus pour être très expressifs, évolutifs et raisonnablement précis, mais leurs performances se détériorent rapidement avec la croissance de l'ensemble d'apprentissage. Un certain nombre de fonctionnalités contribuent au succès des classificateurs naïfs de Bayes. Plus particulièrement, ils ne nécessitent aucun réglage des paramètres du modèle de classification, ils s'adaptent bien à la taille de l'ensemble de données d'apprentissage et ils peuvent facilement gérer les caractéristiques continues.
