Différents types de modèles de régression que vous devez connaître

Les problèmes de régression sont courants dans l'apprentissage automatique, et la technique la plus courante pour les résoudre est l'analyse de régression. Il est basé sur la modélisation des données et implique de déterminer la ligne la mieux ajustée, qui passe par tous les points de données afin que la distance entre la ligne et chaque point de données soit minimale. Bien qu'il existe de nombreuses techniques d'analyse de régression différentes, la régression linéaire et logistique sont les plus importantes. Le type de modèle d'analyse de régression que nous utiliserons dépendra éventuellement de la nature des données concernées.

Découvrons-en plus sur l'analyse de régression et les différents types de modèles d'analyse de régression.

Qu'est-ce que l'analyse de régression ?

L'analyse de régression est une technique de modélisation prédictive permettant de déterminer la relation entre les variables dépendantes (cibles) et les variables indépendantes dans un ensemble de données. Il est généralement utilisé lorsque la variable cible contient des valeurs continues et que les variables dépendantes et indépendantes partagent une relation linéaire ou non linéaire. Ainsi, les techniques d'analyse de régression sont utiles pour déterminer la relation d'effet causal entre les variables, la modélisation des séries chronologiques et les prévisions. Par exemple, la relation entre les ventes et les dépenses publicitaires d'une entreprise peut être mieux étudiée à l'aide d'une analyse de régression.

Types d'analyse de régression

Il existe de nombreux types de techniques d'analyse de régression que nous pouvons utiliser pour faire des prédictions. De plus, l'utilisation de chaque technique dépend de facteurs tels que le nombre de variables indépendantes, la forme de la droite de régression et le type de variable dépendante.

Comprenons quelques-unes des méthodes d'analyse de régression les plus couramment utilisées :

1. Régression linéaire

La régression linéaire est la technique de modélisation la plus connue et suppose une relation linéaire entre une variable dépendante (Y) et une variable indépendante (X). Il établit cette relation linéaire à l'aide d'une ligne de régression, également appelée ligne de meilleur ajustement. La relation linéaire est représentée par l'équation Y = c+m*X + e, où 'c' est l'ordonnée à l'origine, 'm' est la pente de la droite et 'e' est le terme d'erreur.

Le modèle de régression linéaire peut être simple (avec une variable dépendante et une variable indépendante) ou multiple (avec une variable dépendante et plusieurs variables indépendantes).

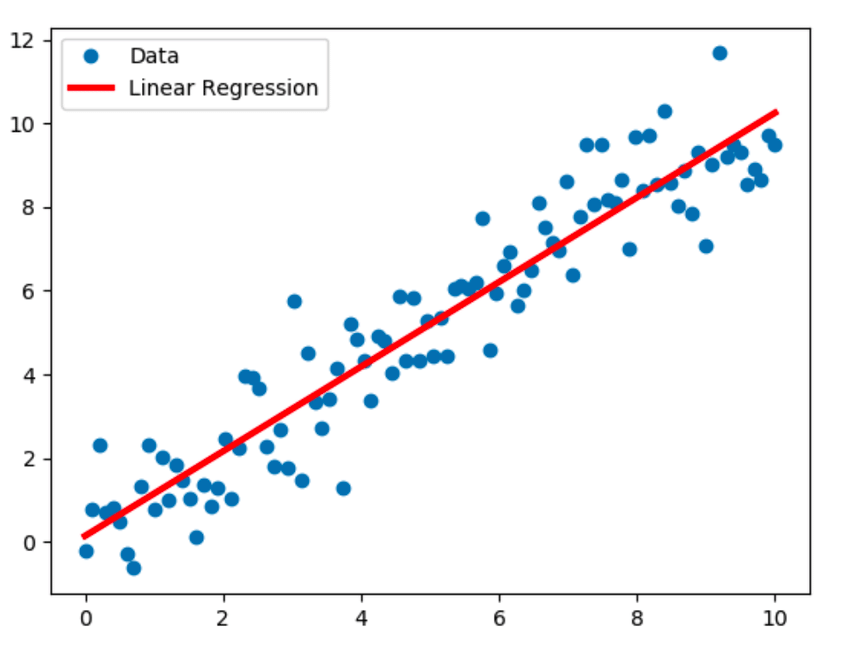
La source

2. Régression logistique

La technique d'analyse de régression logistique trouve une utilisation lorsque la variable dépendante est discrète. En d'autres termes, cette technique est utilisée pour estimer la probabilité d'événements mutuellement exclusifs tels que réussite/échec, vrai/faux, 0/1, etc. Par conséquent, la variable cible ne peut avoir qu'une des deux valeurs, et une courbe sigmoïde représente sa relation avec la variable indépendante. La valeur de la probabilité est comprise entre 0 et 1.

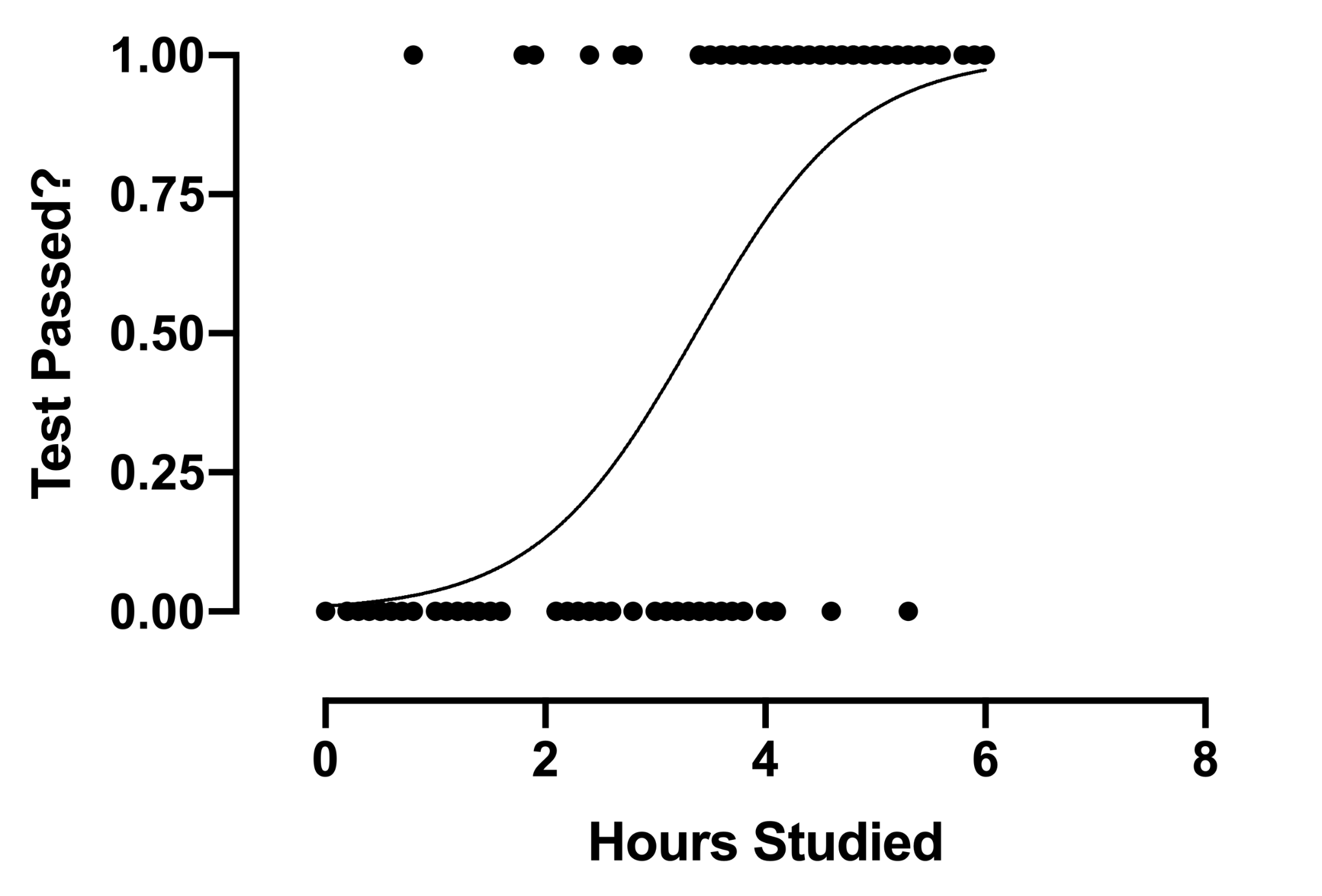
La source

3. Régression polynomiale

La technique d'analyse de régression polynomiale modélise une relation non linéaire entre les variables dépendantes et indépendantes. Il s'agit d'une forme modifiée du modèle de régression linéaire multiple, mais la ligne de meilleur ajustement qui passe par tous les points de données est courbe et non droite.

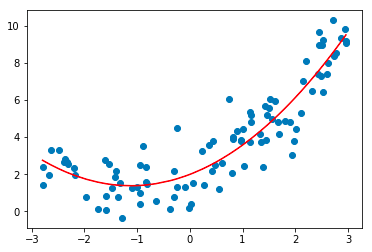
La source

4. Régression de crête

La technique d'analyse de régression de crête est utilisée lorsque les données montrent une multicolinéarité ; c'est-à-dire que les variables indépendantes sont fortement corrélées. Bien que les estimations des moindres carrés en multicolinéarité soient sans biais, leurs variances sont suffisamment grandes pour dévier la valeur observée de la valeur réelle. La régression Ridge minimise les erreurs types en introduisant un degré de biais dans les estimations de régression.

Le lambda (λ) dans l'équation de régression de crête résout le problème de multicolinéarité.

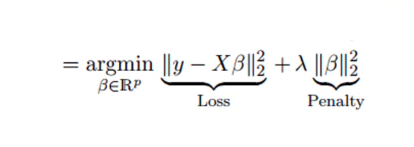
La source

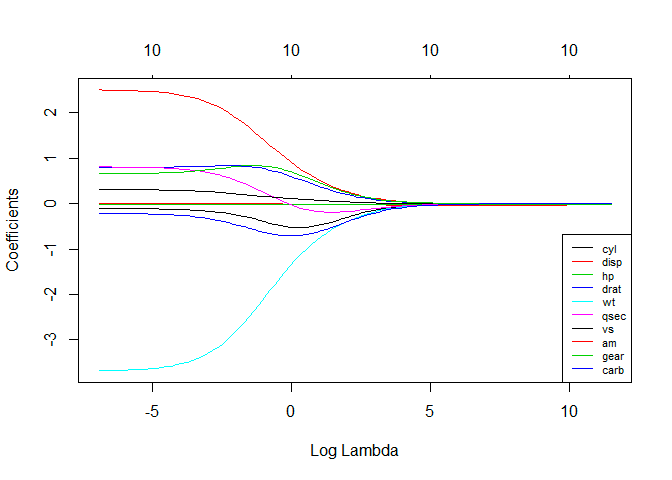
La source

5. Régression au lasso

Comme la régression ridge, la technique de régression lasso (Least Absolute Shrinkage and Selection Operator) pénalise la taille absolue du coefficient de régression. De plus, la technique de régression au lasso utilise une sélection de variables, ce qui entraîne une diminution des valeurs de coefficient vers le zéro absolu.

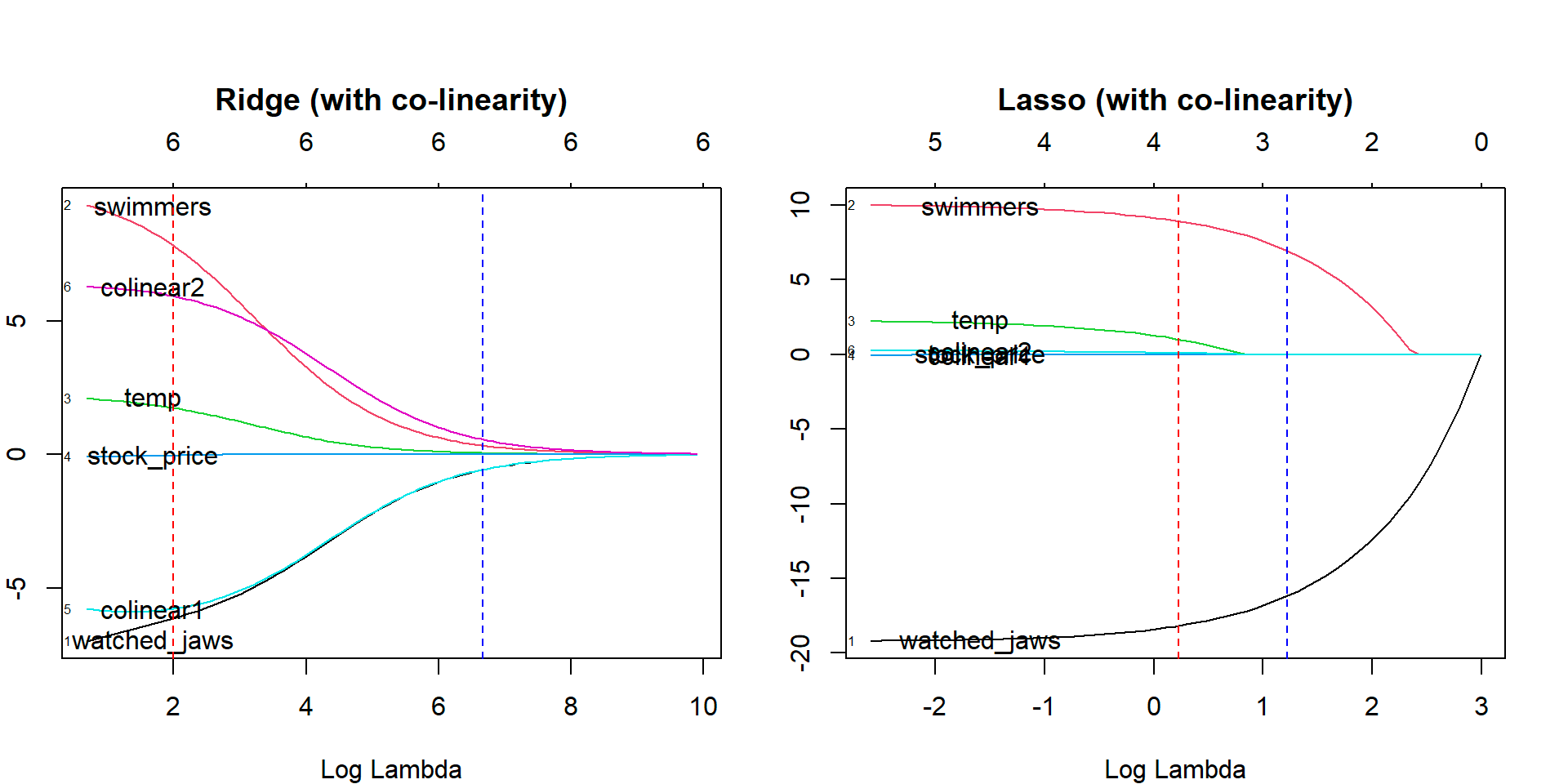
La source

6. Régression quantile

La technique d'analyse de régression quantile est une extension de l'analyse de régression linéaire. Il est utilisé lorsque les conditions de la régression linéaire ne sont pas remplies ou que les données comportent des valeurs aberrantes. La régression quantile trouve des applications en statistique et en économétrie.

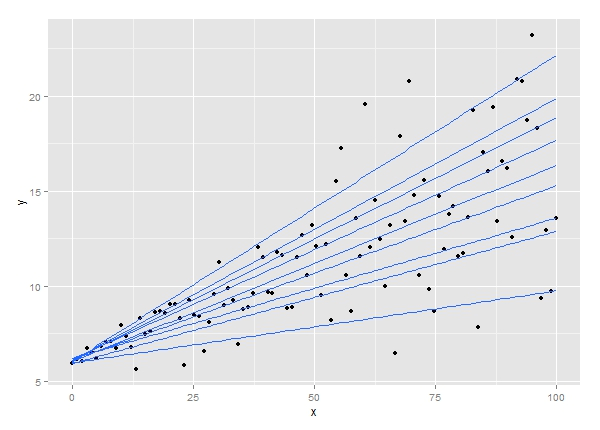
La source

7. Régression linéaire bayésienne

La régression linéaire bayésienne est l'un des types de techniques d'analyse de régression dans l'apprentissage automatique qui utilise le théorème de Bayes pour déterminer la valeur des coefficients de régression. Au lieu de trouver les moindres carrés, cette technique détermine la distribution a posteriori des caractéristiques. En conséquence, la technique a plus de stabilité que la simple régression linéaire.

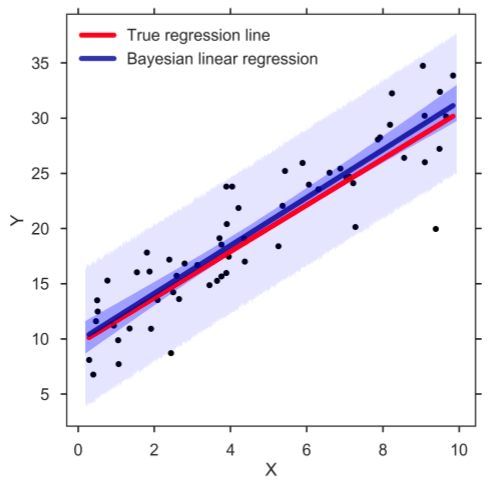
La source

8. Régression en composantes principales

La technique de régression des composantes principales est généralement utilisée pour analyser les données de régression multiple avec multicolinéarité. Comme la technique de régression des crêtes, la méthode de régression des composantes principales minimise les erreurs types en conférant un degré de biais aux estimations de régression. La technique comporte deux étapes : premièrement, l'analyse en composantes principales est appliquée aux données d'apprentissage, puis les échantillons transformés sont utilisés pour former un régresseur.

9. Régression partielle des moindres carrés

La technique de régression des moindres carrés partiels est l'un des types rapides et efficaces de techniques d'analyse de régression basées sur la covariance. Il est bénéfique pour les problèmes de régression où le nombre de variables indépendantes est élevé avec une multicolinéarité probable entre les variables. La technique réduit les variables à un plus petit ensemble de prédicteurs, qui sont ensuite utilisés pour effectuer une régression.

10. Régression nette élastique

La technique de régression nette élastique est un hybride des modèles de régression de crête et de lasso et est utile lorsqu'il s'agit de variables fortement corrélées. Il utilise les pénalités des méthodes de régression ridge et lasso pour régulariser les modèles de régression.

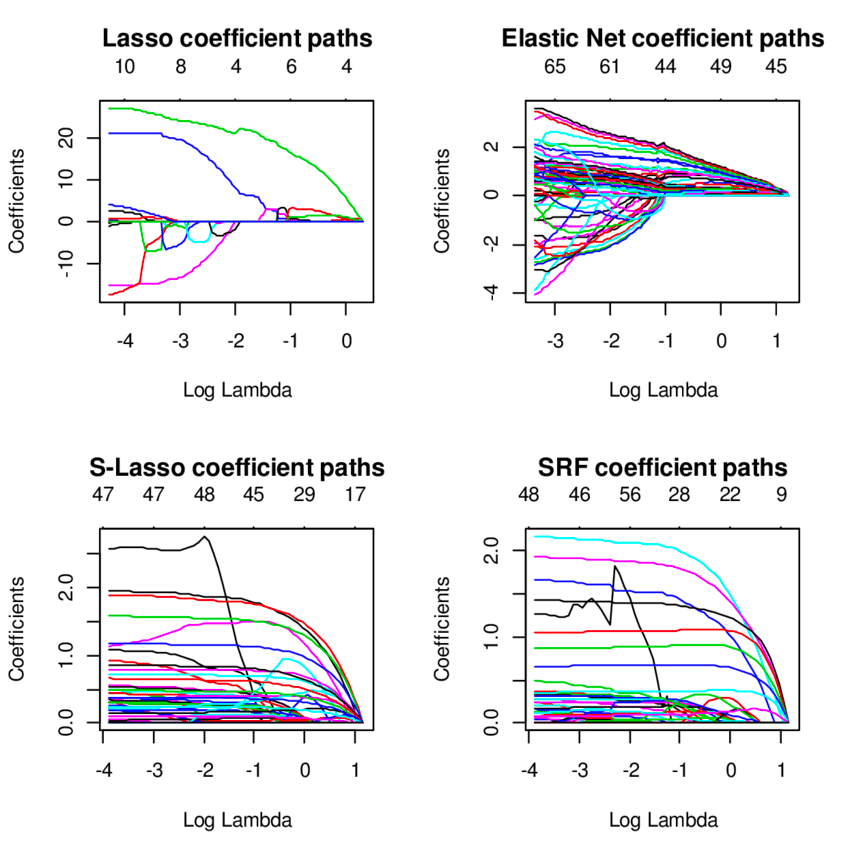
La source

Sommaire

Outre les techniques d'analyse de régression dont nous avons discuté ici, plusieurs autres types de modèles de régression sont utilisés dans l'apprentissage automatique, tels que la régression écologique, la régression pas à pas, la régression jackknife et la régression robuste. Le cas d'utilisation spécifique de tous ces différents types de techniques de régression dépend de la nature des données disponibles et du niveau de précision qui peut être atteint. Dans l'ensemble, l'analyse de régression présente deux avantages principaux. Ceux-ci sont les suivants :

• Il indique la relation entre une variable dépendante et une variable indépendante.

• Il montre la force de l'impact des variables indépendantes sur une variable dépendante.

Aller de l'avant : décrochez une maîtrise ès sciences en apprentissage automatique et IA

Êtes-vous à la recherche d'un programme en ligne complet pour vous préparer à une carrière en apprentissage automatique et en intelligence artificielle?

upGrad propose une maîtrise ès sciences en apprentissage automatique et IA en association avec l'Université John Moores de Liverpool et l'IIIT Bangalore pour former des professionnels de l'IA et des scientifiques des données polyvalents.

Le programme en ligne complet de 20 mois est spécialement conçu pour les professionnels qui souhaitent maîtriser des concepts et des compétences avancés tels que l'apprentissage en profondeur, la PNL, les modèles graphiques, l'apprentissage par renforcement, etc. En outre, le programme vise à donner une base solide en statistiques ainsi que des langages de programmation et des outils clés tels que Python, Keras, TensorFlow, Kubernetes, MySQL, etc.

Faits saillants du programme :

• Master de l'Université John Moores de Liverpool
• PGP exécutif de l'IIIT Bangalore
• Plus de 40 sessions en direct, plus de 12 études de cas et projets, 11 missions de codage, six projets de synthèse
• Plus de 25 séances de mentorat avec des experts de l'industrie
• Assistance professionnelle à 360 degrés et soutien à l'apprentissage
• Opportunités de réseautage entre pairs

Avec une faculté, une pédagogie, une technologie et des experts de l'industrie de classe mondiale, upGrad est devenue la plus grande plate-forme EdTech supérieure d'Asie du Sud et a touché plus de 500 000 professionnels actifs dans le monde. Inscrivez-vous aujourd'hui pour faire partie de la base mondiale de plus de 40 000 apprenants d'upGrad dans plus de 80 pays !