Mise à niveau de l'animation CSS avec des courbes de mouvement

Il y a une animation de l'interface utilisateur, puis une bonne animation de l'interface utilisateur. Une bonne animation vous fait dire "Wow!" - c'est lisse, beau et, surtout, naturel, pas en bloc, rigide ou robotique. Si vous fréquentez Dribbble ou UpLabs, vous saurez de quoi je parle.

Lectures complémentaires sur le Smashing :

• Animations SVG et CSS avec clip-path
• Techniques d'animation pratiques
• Création d'animations "dessinées à la main" avec SVG
• La nouvelle API d'animation Web

Avec autant de concepteurs incroyables créant de si belles animations, tout développeur voudrait naturellement les recréer dans ses propres projets. Maintenant, CSS fournit des préréglages pour transition-timing-function , tels que ease-in , ease-out et ease-in-out , qui ajoutent un certain niveau de douceur et de réalisme, mais ils sont très génériques, n'est-ce pas ? À quel point ce serait ennuyeux si chaque animation sur le Web suivait les trois mêmes fonctions de synchronisation ?

L'une des propriétés de transition-timing-function est cubic-bezier(n1, n2, n3, n4) , dans laquelle vous pouvez passer quatre nombres pour créer votre propre fonction de synchronisation. Vers la fin de cet article, vous saurez exactement ce que ces quatre nombres représentent - mais croyez-moi, trouver quatre nombres pour capturer la transition que vous imaginez dans votre tête est loin d'être facile. Mais grâce à cubic-bezier et Ceasar, vous n'avez pas à le faire. Ces outils apportent des courbes de mouvement sur le Web.

Les courbes de mouvement sont principalement utilisées par les animateurs (par exemple, dans Adobe After Effects) pour créer des animations avancées et réalistes. Avec cubic-bezier et Ceasar, vous pouvez simplement manipuler la forme d'une courbe, et ces quatre nombres ( n1, n2, n3, n4 ) seront remplis pour vous, ce qui est absolument génial ! Néanmoins, pour utiliser et tirer le meilleur parti des courbes de mouvement, vous devez comprendre leur fonctionnement, et c'est ce que nous allons faire dans cet article. Commençons.

Comprendre les courbes de mouvement

Une courbe de mouvement n'est rien d'autre qu'un tracé entre une propriété animable et le temps. Une courbe de mouvement définit comment la vitesse d'une animation s'exécutant sous son influence varie dans le temps.

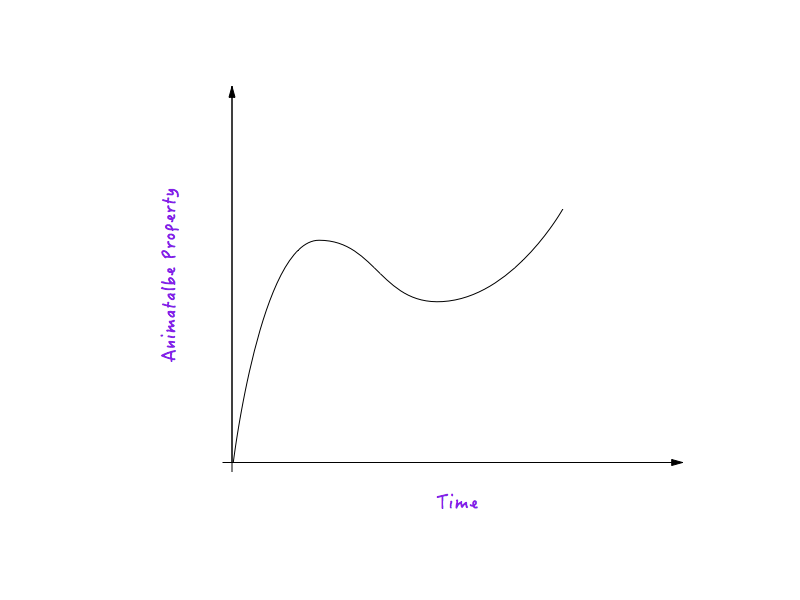
Prenons distance ( translateX ) comme exemple de propriété animable. (L'explication est valable pour toute autre propriété animable.)

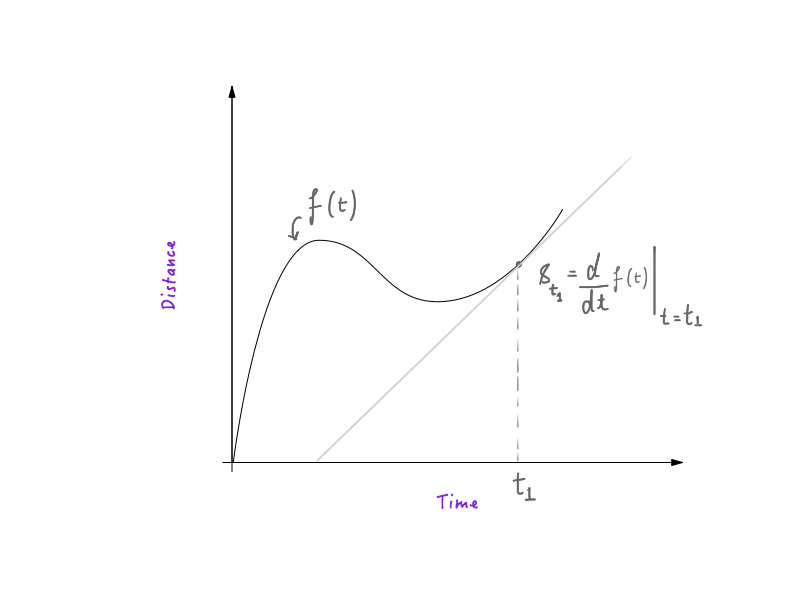
Si vous avez de l'expérience en physique et en calcul de base, vous saurez que déchiffrer la vitesse à partir d'un graphique distance-temps est très simple. La première dérivée de la distance en fonction du temps , par rapport au temps , est la vitesse, ce qui signifie qu'un objet suivant une courbe distance-temps aurait une vitesse plus grande aux endroits où la courbe est raide et plus faible aux endroits où la courbe est plus plate . Si vous savez comment cela fonctionne, tant mieux ! Vous êtes prêt et pouvez passer à la section suivante.

Maintenant, je suis conscient que la conception et le développement sont un domaine diversifié et que tout le monde n'a pas le même parcours. Peut-être que les deux paragraphes ci-dessus n'étaient que du jargon pour vous. Ne vous inquiétez pas. Nous allons continuer et donner un sens au jargon.

Considérez la boîte rouge ci-dessous. Soyons un peu insensibles ici et appelons la boîte rouge « Boxy » ; ce sera plus facile de s'y référer ainsi. D'accord, alors Boxy va se déplacer d'un bord à l'autre de l'écran de façon linéaire, et nous allons analyser son mouvement.

L'un des préréglages de transition-timing-function est linear . Pour faire bouger Boxy, il suffit d'ajouter la classe suivante.

 .moveForward { transform: translateX(1000px); }

Pour contrôler l'animation, nous définirions la propriété de transition pour Boxy comme suit :

 #boxy { width: 200px; height: 200px; background: red; transition-property: transform; transition-duration: 1s; transition-timing-function: linear; }

C'est une façon très détaillée de spécifier transition . En réalité, vous trouverez presque toujours transition écrite sous sa forme abrégée :

 #boxy { width: 200px; height: 200px; background: red; transition: transform 1s linear; }

Voyons aller.

Robotique, n'est-ce pas ? On pourrait dire que ce mouvement semble robotique parce qu'il est linéaire, ce qui est une réponse parfaitement plausible. Mais pourriez-vous expliquer pourquoi? Nous pouvons voir que le réglage linear entraîne un mouvement robotique, mais que se passe-t-il exactement derrière la scène ? C'est ce que nous allons découvrir en premier ; nous allons entrer dans les entrailles et comprendre pourquoi ce mouvement semble robotique, en bloc et non naturel.

Commençons par représenter graphiquement le mouvement de Boxy pour voir si nous pouvons avoir un aperçu. Notre graphique aura deux axes, le premier étant la distance et le second le temps. Boxy couvre une distance totale de 1000 pixels (distance) en 1 seconde (temps). Maintenant, ne soyez pas effrayé par tous les calculs ci-dessous - c'est très simple.

Voici notre graphique très simple, avec les axes comme mentionné.

Pour l'instant, c'est vide. Complétons-le avec quelques données.

Pour commencer, on sait qu'à 0 seconde, alors que l'animation n'a pas encore commencé, Boxy est dans sa position initiale (0 pixel). Et après 1 seconde, Boxy a parcouru un total de 1000 pixels, atterrissant sur le bord opposé de l'écran.

Traçons ces données sur le graphique.

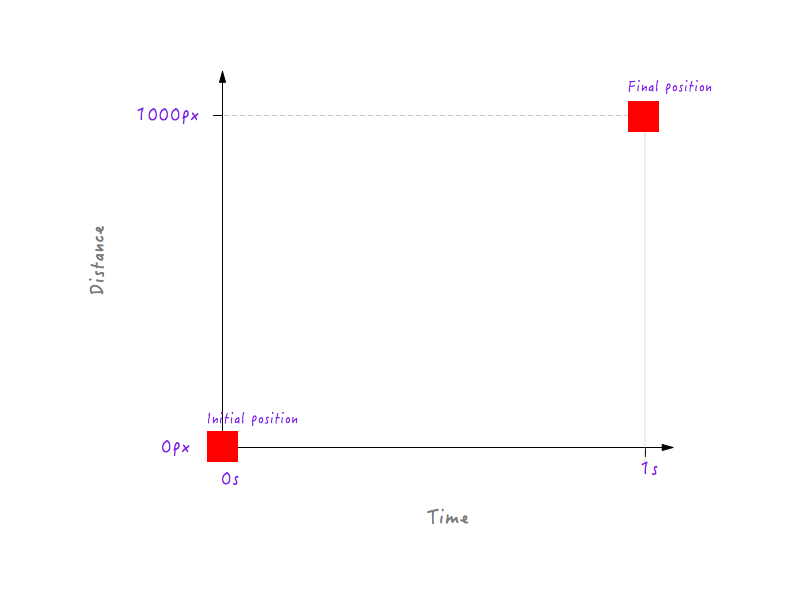
Jusqu'ici tout va bien. Mais deux points de données ne suffisent pas - nous avons besoin de plus. La figure suivante montre les positions de Boxy à différents moments (tout cela grâce à ma caméra à grande vitesse).

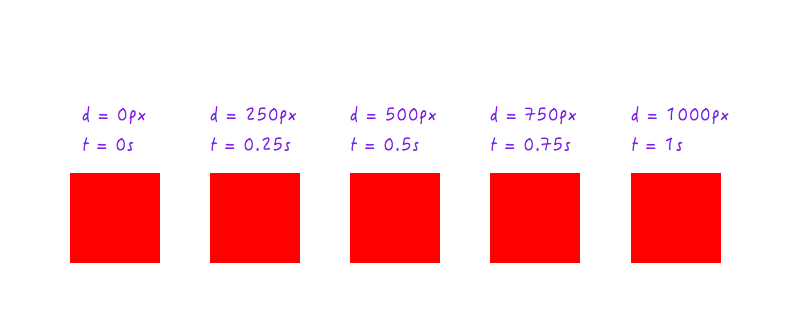
Ajoutons ces données à notre graphique.

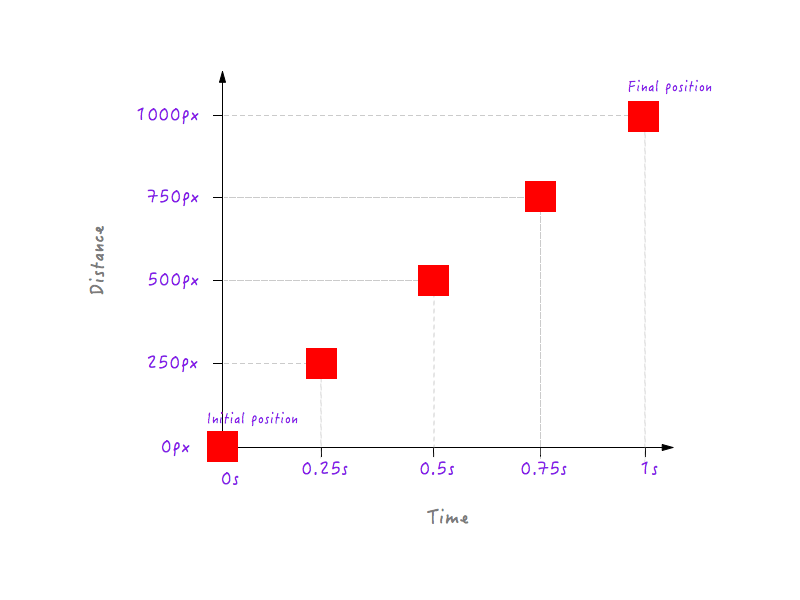
Vous pourriez, bien sûr, avoir beaucoup plus de points de données pour des temps différents (par exemple, 0,375 seconde, 0,6 seconde, etc.), mais ce que nous avons est suffisant pour compléter notre graphique. En joignant tous les points, nous avons complété le graphique. Tape m'en cinq!

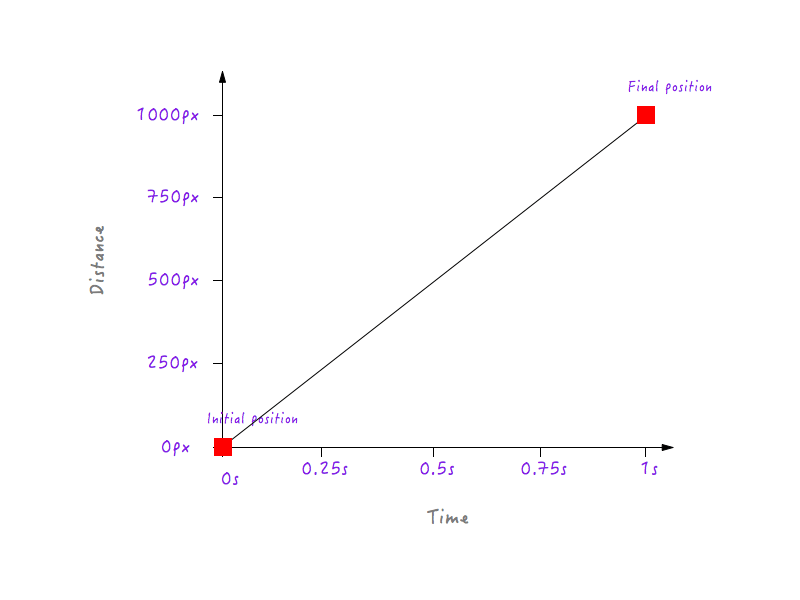
Cool, mais qu'est-ce que cela nous dit? Rappelez-vous que nous avons commencé notre enquête dans le but de comprendre pourquoi le mouvement linéaire de Boxy semble non naturel et robotique ? En un coup d'œil, ce graphique que nous venons de construire ne nous dit rien à ce sujet. Nous devons aller plus loin.

Gardez le graphique à l'esprit et parlons une minute de la vitesse. Je sais que vous savez ce qu'est la vitesse — j'aimerais juste l'exprimer en termes mathématiques. En fait, la formule de la vitesse est la suivante :

Ainsi, si une voiture parcourt une distance de 100 kilomètres en 1 heure, on dit que sa vitesse est de 100 kilomètres par heure.

Si la voiture double sa vitesse, elle commencera à parcourir le double de la distance (200 kilomètres) dans le même intervalle (1 heure), ou, en d'autres termes, elle couvrira la distance initiale de 100 kilomètres en la moitié du temps (0,5 heure) . Avoir du sens ?

De même, si la voiture réduisait de moitié sa vitesse (c'est-à-dire qu'elle ralentissait de moitié), elle commencerait à parcourir une distance de 50 kilomètres dans le même intervalle (1 heure), ou, en d'autres termes, elle parcourrait la distance initiale de 100 kilomètres en deux fois plus de temps (2 heures).

Génial! Avec cela à l'écart, reprenons là où nous nous sommes arrêtés. Nous essayions de comprendre comment le graphique entre la distance et le temps peut nous aider à comprendre pourquoi le mouvement linéaire de Boxy semble robotique.

Hé, attendez une seconde ! Nous avons un graphique entre la distance et le temps, et la vitesse peut être calculée à partir de la distance et du temps, n'est-ce pas ? Essayons de calculer la vitesse de Boxy à différents intervalles de temps.

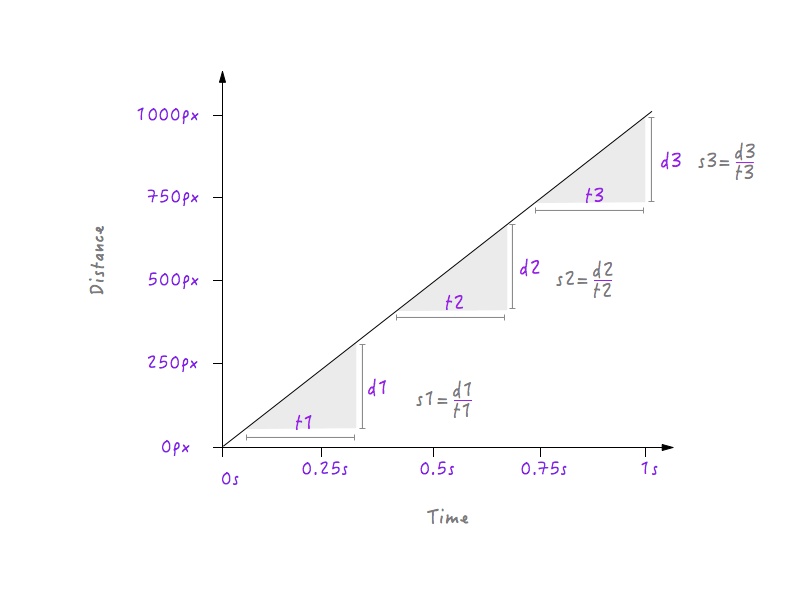
Ici, j'ai choisi trois intervalles de temps différents : un près du début, un au milieu et un à la fin près de la position finale. Comme on le voit, aux trois intervalles, Boxy a exactement la même vitesse (s1 = s2 = s3) de 1000 pixels par seconde ; c'est-à-dire que quel que soit l'intervalle que vous choisissez dans le graphique ci-dessus, vous trouverez Boxy se déplaçant à 1000 pixels par seconde. N'est-ce pas étrange ? Les choses dans la vraie vie ne bougent pas à une vitesse constante ; ils démarrent lentement, augmentent progressivement leur vitesse, se déplacent pendant un certain temps, puis ralentissent à nouveau avant de s'arrêter, mais Boxy démarre brusquement à une vitesse de 1000 pixels par seconde, se déplaçant à la même vitesse et s'arrêtant brusquement exactement à la même vitesse. C'est pourquoi le mouvement de Boxy semble robotique et contre nature. Nous allons devoir changer notre graphique pour résoudre ce problème. Mais avant de plonger, nous devrons savoir comment les changements de vitesse affecteront le graphique tracé entre la distance et le temps. Prêt? Cela va être amusant.

Doublez la vitesse de Boxy et voyons comment l'apparence du graphique change en réponse. La vitesse d'origine de Boxy, comme nous l'avons calculé ci-dessus, est de 1000 pixels par seconde. Parce que nous avons doublé la vitesse, Boxy pourra désormais couvrir la distance de 1000 pixels en deux fois moins de temps, c'est-à-dire en 0,5 seconde. Mettons cela sur un graphique.

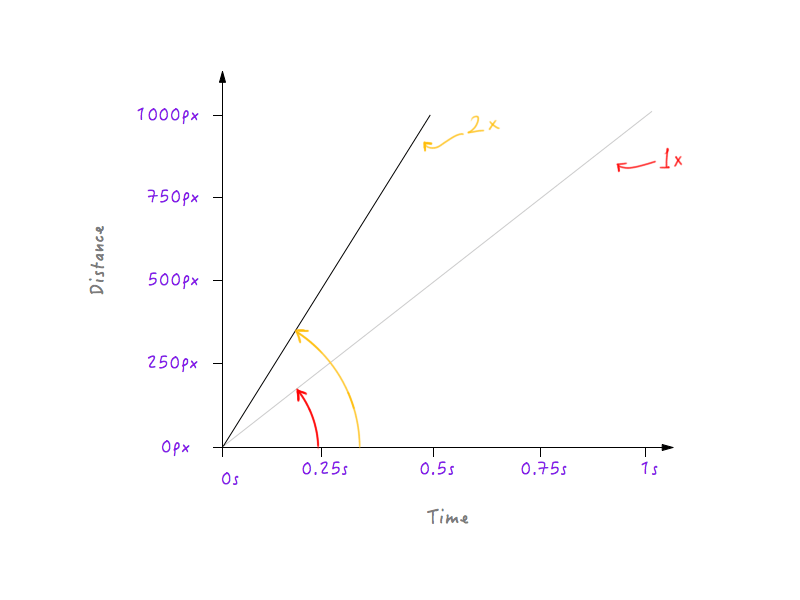
Et si on triplait la vitesse ? Boxy couvre désormais 1000 pixels en un tiers du temps (un tiers de seconde).

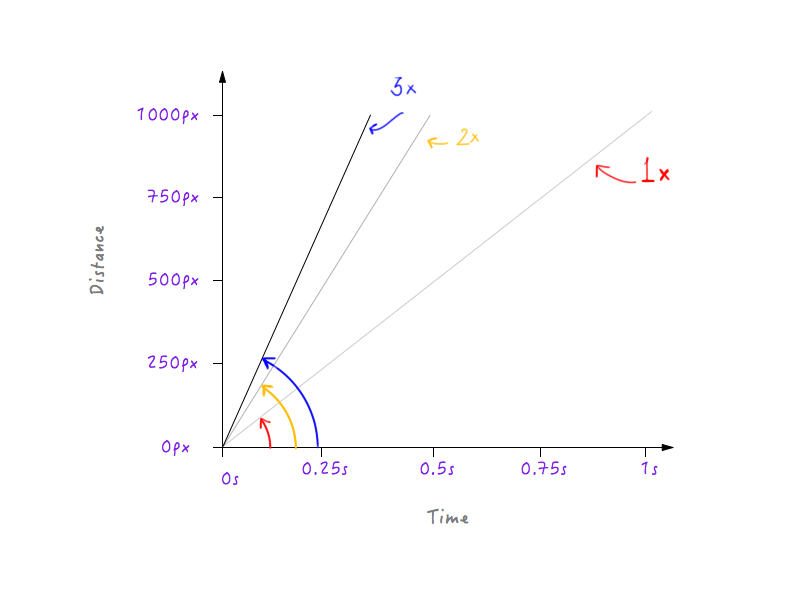
Hum, remarquez quelque chose ? Remarquez comment, lorsque le graphique change, l'angle que fait la ligne avec l'axe du temps augmente à mesure que la vitesse augmente.

Très bien, allons-y et réduisons de moitié la vitesse de Boxy. Réduire de moitié sa vitesse signifie que Boxy ne pourra couvrir que 500 pixels (la moitié de la distance d'origine) en 1 seconde. Mettons cela sur un graphique.

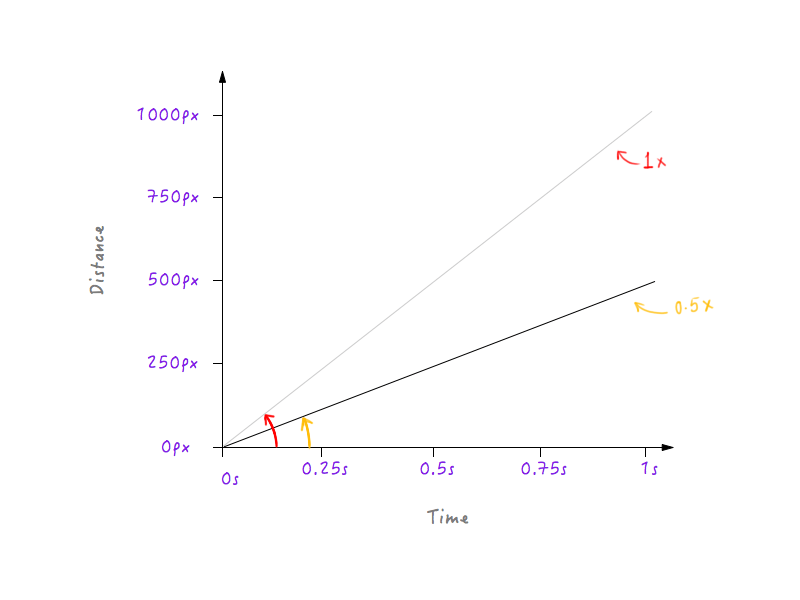
Ralentissons Boxy un peu plus, ce qui rend la vitesse un tiers de l'original. Boxy pourra couvrir un tiers de la distance initiale en 1 seconde.

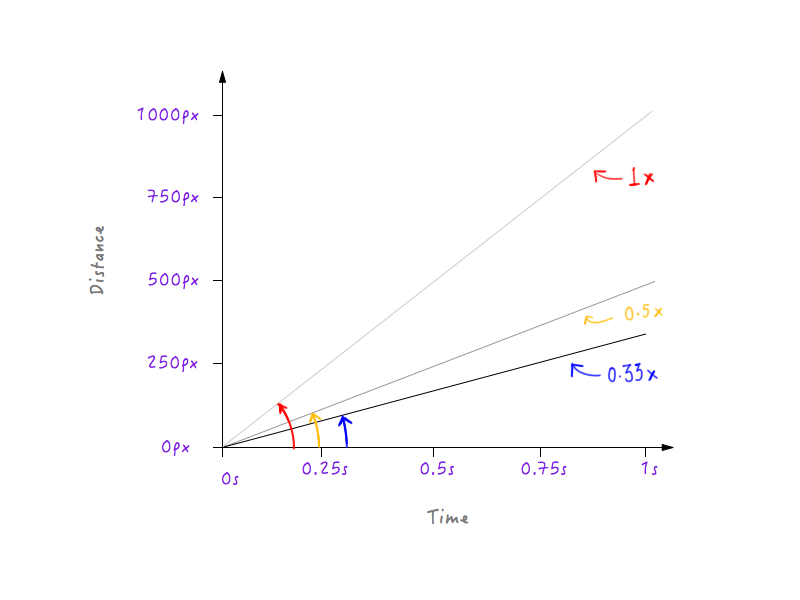
Voir un modèle? La ligne devient de plus en plus raide à mesure que nous augmentons la vitesse de Boxy et commence à s'aplatir à mesure que nous ralentissons Boxy.

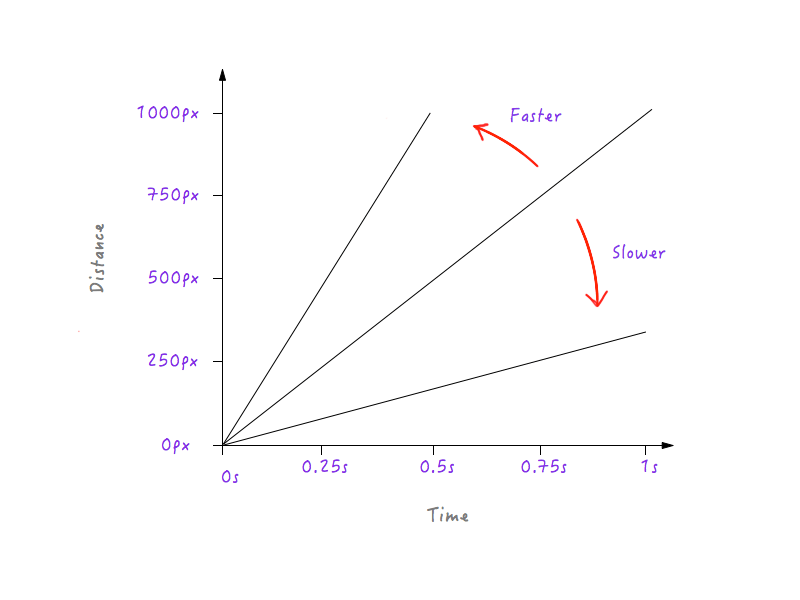
Cela a du sens car, pour une ligne plus raide, une petite progression dans le temps produit un changement de distance beaucoup plus important, impliquant une plus grande vitesse.

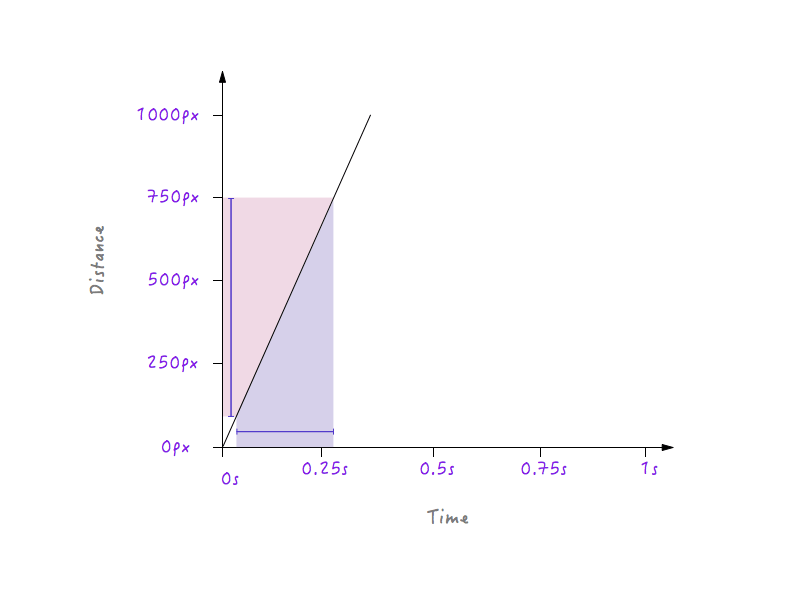
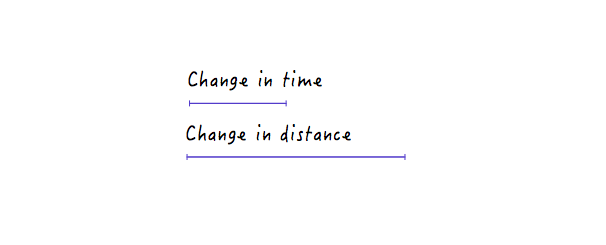
En revanche, pour une ligne moins raide, un grand changement de temps ne produit qu'un petit changement de distance, c'est-à-dire une vitesse plus faible.

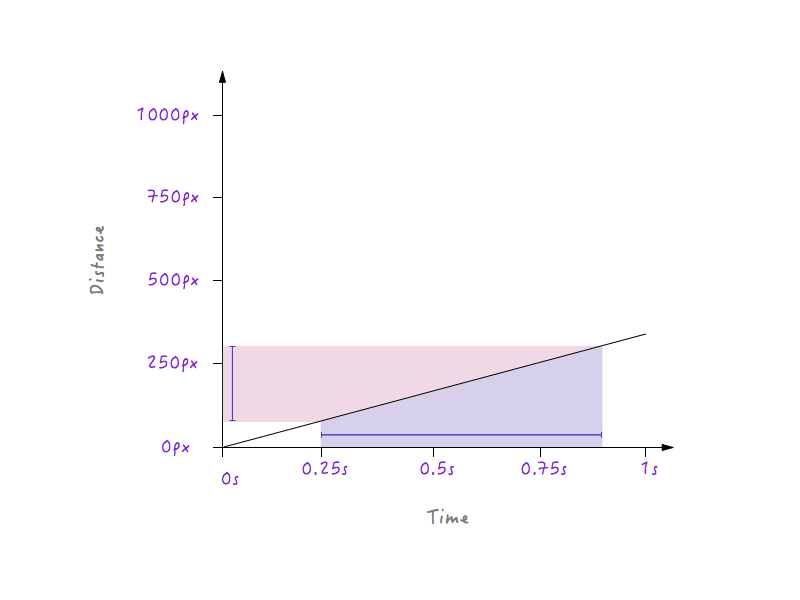
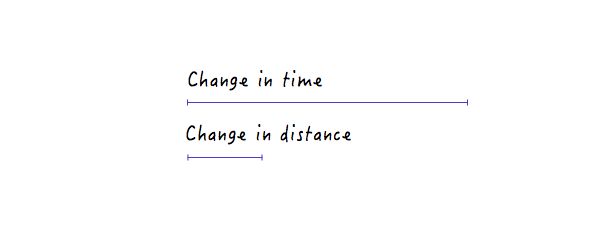
Avec tous les changements que nous avons apportés, Boxy se déplace toujours de manière linéaire, juste à des vitesses différentes. Cependant, avec nos connaissances nouvellement acquises sur la façon dont les changements de distance par rapport au temps peuvent affecter la vitesse, nous pouvons expérimenter et dessiner un graphique qui fait bouger Boxy d'une manière qui semble naturelle et réaliste.

Allons-y étape par étape. Tout d'abord, les choses dans la vraie vie commencent lentement et augmentent lentement en vitesse. Alors, faisons cela.

Dans toutes les itérations du graphique ci-dessous, vous remarquerez que les points aux coins opposés restent fixes. En effet, nous ne modifions pas la durée d'exécution de l'animation, ni la distance parcourue par Boxy.

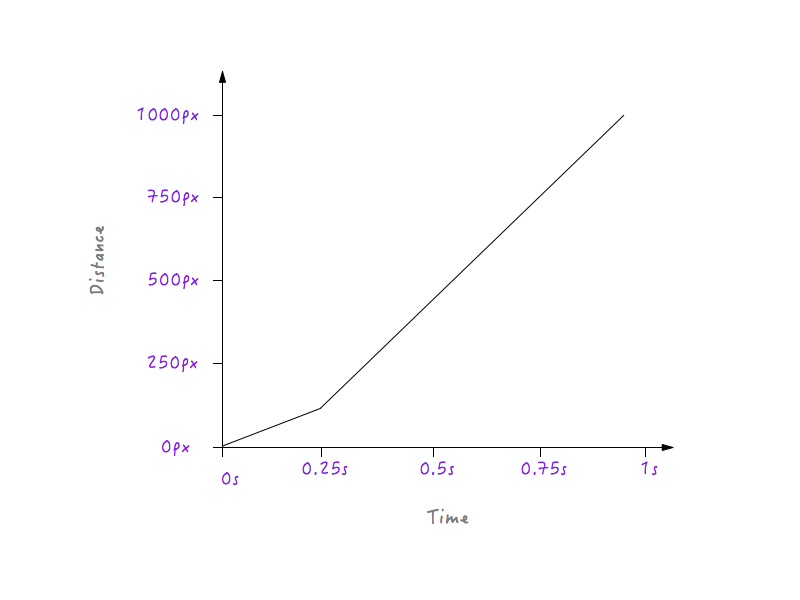
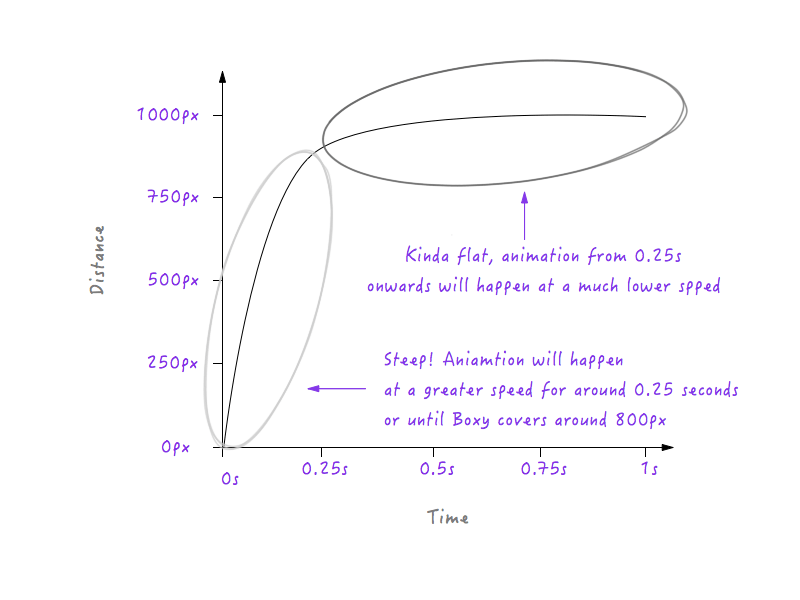
Si Boxy doit suivre le graphique ci-dessus, il se déplacera à une vitesse plus lente pendant 0,25 seconde, car la ligne est moins raide à partir de 0 à 0,25 seconde, puis il passera brusquement à une vitesse plus élevée après 0,25 seconde (la raison étant que la ligne du graphique devient plus raide après 0,25 seconde). Nous devrons cependant adoucir cette transition; nous ne voulons pas de coins — c'est ce qu'on appelle une courbe de mouvement, après tout. Convertissons ce coin en courbe.

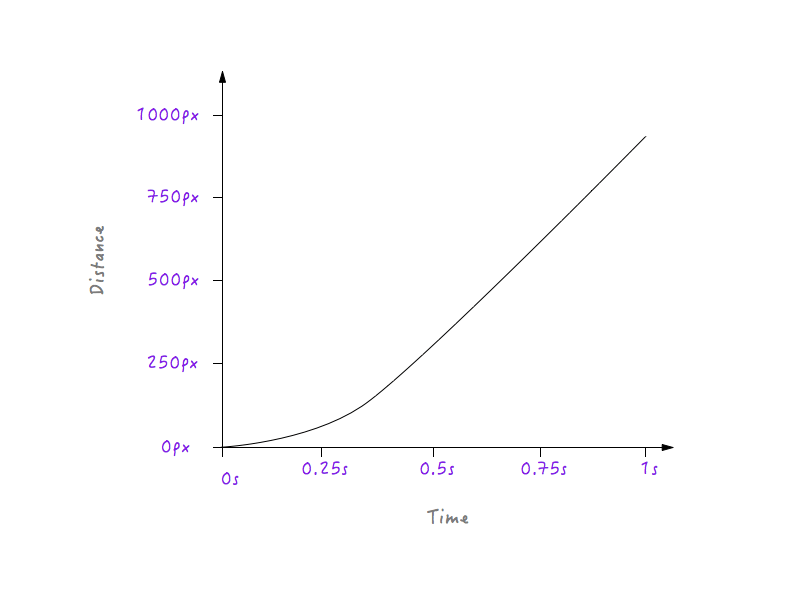
Remarquez la transition en douceur que Boxy subit du repos à l'augmentation progressive de la vitesse.

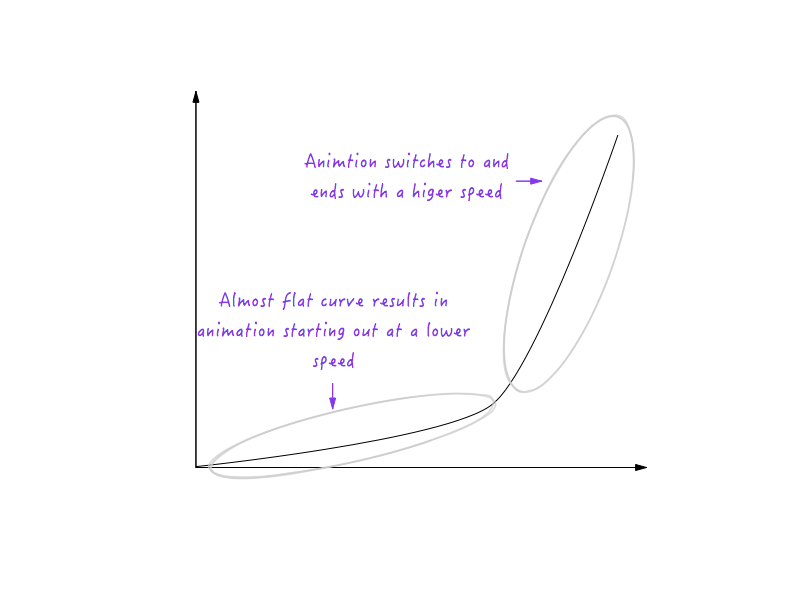
Bien! Ensuite, les objets de la vie réelle ralentissent progressivement avant de s'arrêter. Modifions le graphique pour que cela se produise. Encore une fois, nous choisirons un moment après lequel nous aimerions que Boxy commence à ralentir. Que diriez-vous d'environ 0,6 seconde ? J'ai déjà lissé le coin de la transition vers une courbe ici.

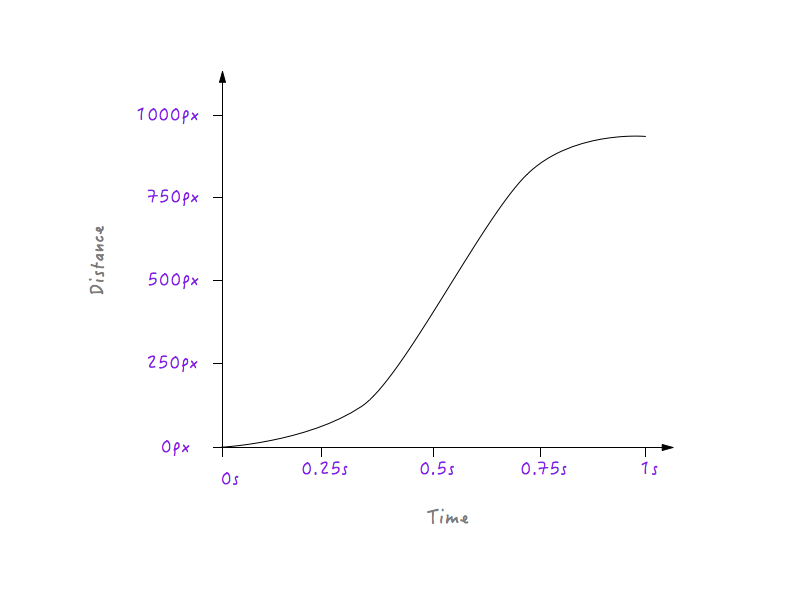
Regarde Boxy go ! Beaucoup plus naturel, n'est-ce pas ?

La courbe que nous avons dessinée à la place du coin est en fait une collection de nombreux petits segments de ligne ; et, comme vous le savez déjà, plus la ligne est raide sur le graphique, plus la vitesse est élevée, et plus la ligne est plate, plus la vitesse est lente. Remarquez comment dans la partie gauche de l'image, les segments de ligne qui composent la courbe deviennent de plus en plus raides, entraînant une augmentation progressive de la vitesse, et s'aplatissent progressivement sur le côté droit, entraînant une diminution progressive de la vitesse ?

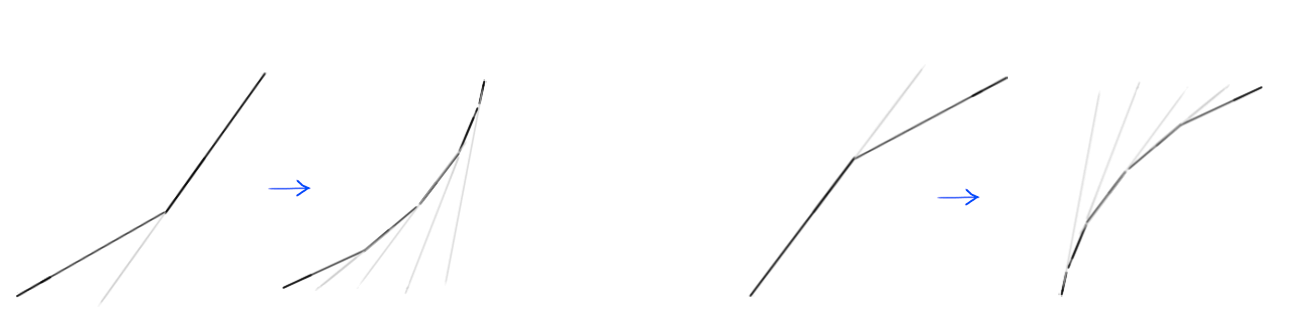
Avec toutes ces connaissances, donner un sens aux courbes de mouvement devient beaucoup plus facile. Regardons quelques exemples.

Utilisation des courbes de mouvement dans l'animation de l'interface utilisateur

La prochaine fois que vous devrez animer un élément de l'interface utilisateur, vous aurez à votre disposition la puissance des courbes de mouvement. Qu'il s'agisse d'une barre coulissante, d'une fenêtre modale ou d'un menu déroulant, ajouter la bonne quantité d'animation et la rendre fluide et naturelle augmentera considérablement la qualité de votre interface utilisateur. Cela rendra l'interface utilisateur agréable. Prenez le menu coulissant ci-dessous :

Cliquer sur le menu hamburger fait apparaître le menu de gauche, mais l'animation semble en bloc. La ligne 51 du CSS montre que l'animation a transition-timing-function définie sur linear . Nous pouvons améliorer cela. Passons à cubic-bezier et créons une fonction de synchronisation personnalisée.

Si vous lisez ceci, il est prudent de supposer que vous êtes un concepteur ou un développeur ou les deux et, par conséquent, que vous n'êtes pas étranger aux courbes de Bézier cubiques ; il y a de fortes chances que vous les ayez rencontrés au moins une fois. Les courbes de Bézier sont une merveille. Ils sont principalement utilisés en infographie pour dessiner des formes et sont utilisés dans des outils tels que Sketch et Adobe Illustrator pour dessiner des graphiques vectoriels. La raison pour laquelle les courbes de Bézier cubiques sont si populaires est qu'elles sont si faciles à utiliser : modifiez simplement les positions des quatre points différents et créez le type de courbe dont vous avez besoin.

Comme nous connaissons toujours les états initial et final de l'objet animé, nous pouvons fixer deux des points. Cela ne laisse que deux points dont nous devons modifier les positions. Les deux points fixes sont appelés points d'ancrage, et les deux autres sont des points de contrôle.

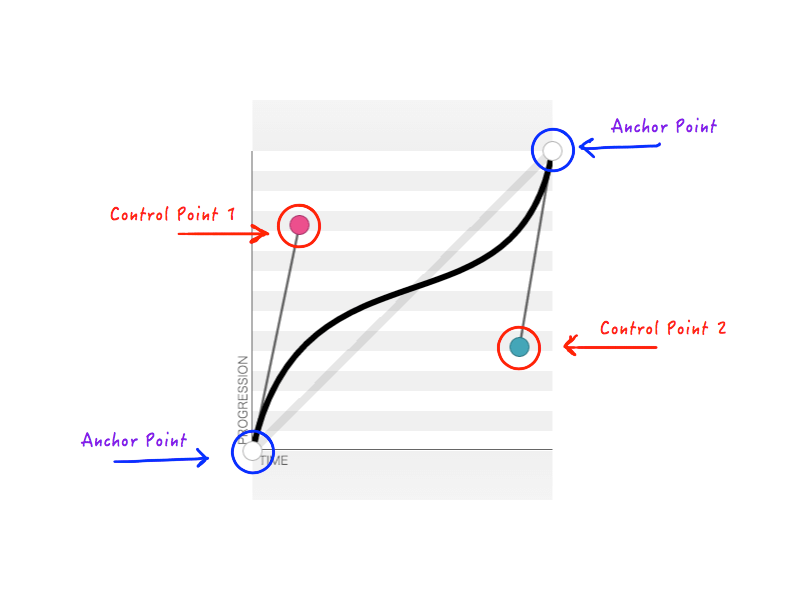
Comme vous vous en souvenez, cubic-bezier accepte quatre nombres ( n1, n2, n3, n4 ) lorsque vous créez une transition-timing-function personnalisée. Ces quatre nombres ne représentent rien d'autre que les positions des deux points de contrôle : n1, n2 représentent les coordonnées x et y du premier point de contrôle, et n3, n4 représentent les coordonnées du second point de contrôle. Étant donné que la modification de la position des points de contrôle modifiera la forme de la courbe et, par conséquent, notre animation dans son ensemble, le résultat est le même lorsque tout ou partie de n1, n2, n3, n4 est modifié. Par exemple, la figure ci-dessous représente cubic-bezier(.14, .78, .89, .35) :

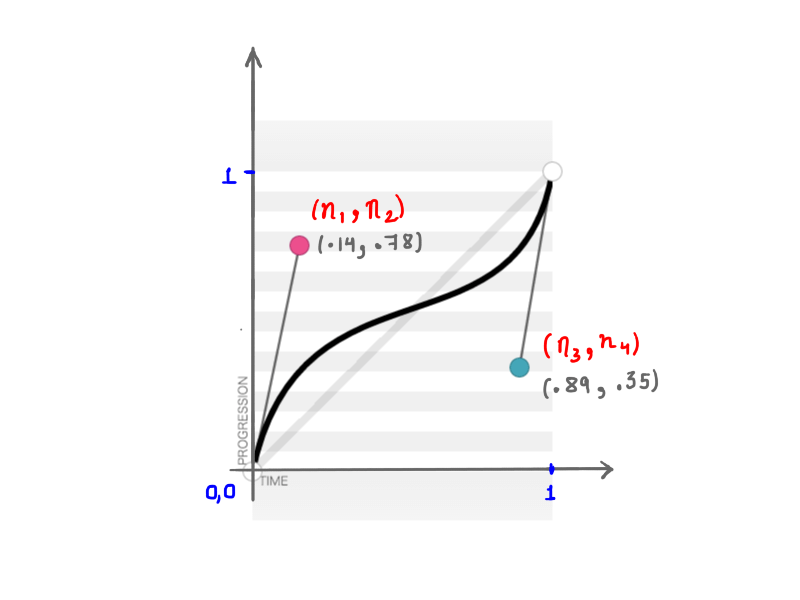
Les mathématiques derrière ces courbes apparemment simples sont fascinantes.

D'accord, d'accord, revenons là où nous allions avec cubic-bezier : créer une transition-timing-function personnalisée. Je veux le genre d'animation dans laquelle le menu glisse très rapidement, puis ralentit gracieusement et se termine :

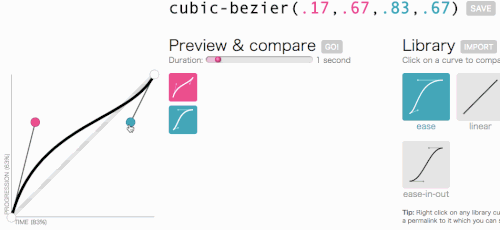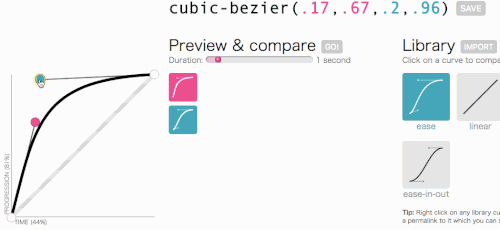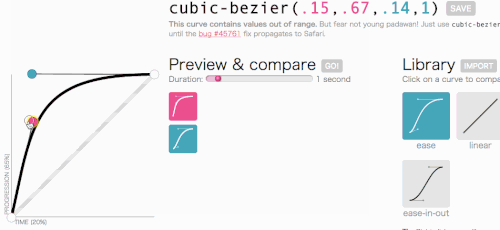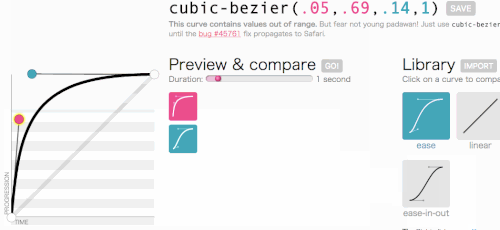
Cela semble bon. L'animation commencera rapidement puis ralentira, plutôt que de se déplacer à une vitesse constante tout au long. Je vais simplement copier cubic-bezier(.05, .69, .14, 1) du haut de la page et remplacer linear par celui-ci.

Regarde la différence? La deuxième itération semble beaucoup plus naturelle et attrayante. Imaginez si chaque animation de votre interface utilisateur suivait une fonction de synchronisation naturelle. À quel point cela serait-il formidable ?

Comme nous l'avons vu, les courbes de mouvement ne sont pas compliquées du tout. Ils sont très faciles à comprendre et à utiliser. Avec eux, vous pouvez faire passer votre interface utilisateur au niveau supérieur.

J'espère que vous avez appris comment fonctionnent les courbes de mouvement. Si vous faisiez beaucoup d'essais et d'erreurs pour que les courbes de mouvement fonctionnent comme vous le souhaitez, ou si vous ne les utilisiez pas du tout, vous devriez maintenant être à l'aise de les plier à votre guise et de créer de belles animations. Parce qu'après tout, l'animation compte.