Statistiques et modèle bayésiens : expliqués

La technique bayésienne est une approche statistique utilisée dans l'analyse des données et l'estimation des paramètres. Cette approche est basée sur le théorème de Bayes.

La statistique bayésienne suit un principe unique dans lequel elle aide à déterminer la distribution de probabilité conjointe pour les paramètres observés et non observés à l'aide d'un modèle statistique. La connaissance des statistiques est essentielle pour résoudre les problèmes analytiques dans ce scénario.

Depuis l'introduction du théorème de Bayes dans les années 1770 par Thomas Bayes, il est resté un outil indispensable en statistique. Les modèles bayésiens remplacent classiquement les modèles fréquentistes, car les innovations récentes en matière de statistiques ont permis de franchir des étapes importantes dans un large éventail d'industries, notamment la recherche médicale, la compréhension des recherches sur le Web et le traitement des langues naturelles (traitement du langage naturel).

Par exemple, la maladie d'Alzheimer est une maladie connue pour présenter un risque progressif à mesure qu'une personne vieillit. Cependant, à l'aide du théorème de Bayes, les médecins peuvent estimer la probabilité qu'une personne ait la maladie d'Alzheimer à l'avenir. Cela s'applique également au cancer et aux autres maladies liées à l'âge auxquelles une personne devient vulnérable au cours des dernières années de sa vie.

Statistiques fréquentes vs statistiques bayésiennes

Statistiques fréquentes vs statistiques bayésiennes ont toujours été un sujet de controverse et de cauchemars pour les débutants, qui ont tous deux du mal à choisir entre les deux. Au début du XXe siècle, les statistiques bayésiennes ont connu leur lot de problèmes de méfiance et d'acceptation. Avec le temps, cependant, les gens ont réalisé l'applicabilité des modèles bayésiens et les solutions précises qu'ils donnent.

Voici un aperçu des statistiques fréquentes et des complexités qui leur sont associées :

Statistiques fréquentes

Il s'agit d'une méthodologie inférentielle largement utilisée dans le monde des statistiques. Il analyse si un événement (mentionné comme hypothèse) a eu lieu ou non. Il estime également la probabilité que l'événement se produise pendant la durée de l'expérience. L'expérience est répétée jusqu'à ce que le résultat souhaité soit atteint.

Leurs échantillons de distribution sont de taille réelle, et l'expérience se répète théoriquement à l'infini. Voici un exemple montrant comment les statistiques de fréquence peuvent être utilisées pour étudier le lancer d'une pièce.

• La possibilité d'obtenir une tête en lançant la pièce une fois est de 0,5 (1/2).
• Le nombre de têtes indique le nombre réel de prospects obtenus.
• La différence entre le nombre réel de faces et le nombre prévu de faces augmentera à mesure que le nombre de lancers augmentera.

Donc ici, le résultat dépend du nombre de fois que l'expérience est répétée. C'est un inconvénient majeur des statistiques fréquentes.

D'autres défauts associés à sa conception et à ses techniques d'interprétation sont devenus évidents au XXe siècle, lorsque l'application de statistiques fréquentes aux modèles numériques était à son apogée.

Limites des statistiques fréquentes

Les trois principaux défauts des statistiques fréquentes sont énumérés ci-dessous :

1. Valeurs p variables

Les valeurs de p mesurées pour un échantillon de taille fixe dans une expérience avec un point final défini changent avec tout changement du point final et de la taille de l'échantillon. Il en résulte deux valeurs p pour une seule donnée qui est incorrecte.

2. Intervalles de confiance incohérents

L'IC (Intervalle de Confiance) dépend uniquement de la taille de l'échantillon. Cela rend le potentiel d'arrêt non pertinent.

3. Valeurs estimées de CI

Les intervalles de confiance ne sont pas une distribution de probabilité et leurs valeurs pour un paramètre ne sont qu'une estimation et non des valeurs réelles.

Les trois raisons ci-dessus ont donné naissance à l'approche bayésienne qui applique les probabilités aux problèmes statistiques.

Naissance des statistiques bayésiennes

Le révérend Thomas Bayes a proposé pour la première fois l'approche bayésienne des statistiques dans son essai écrit en 1763. Cette approche a été publiée par Richard Price en tant que stratégie en probabilité inverse pour prévoir les événements futurs en fonction du passé.

L'approche est basée sur le théorème de Bayes qui est expliqué ci-dessous :

Théorème de Bayes

L'axiome de probabilité de Renyi examine les probabilités conditionnelles, où les possibilités que l'événement A et l'événement B se produisent sont dépendantes ou conditionnelles. La probabilité conditionnelle de base peut s'écrire :

La probabilité que l'événement B se produise dépend de l'événement A.

L'équation ci-dessus est le fondement de la règle de Bayes, une expression mathématique du théorème de Bayes qui stipule :

Ici, ∩ désigne l'intersection.

La règle de Bayes peut s'écrire :

La règle de Bayes est le fondement des statistiques bayésiennes, où les informations disponibles sur un paramètre particulier dans un modèle statistique sont comparées et mises à jour avec les données collectées.

Les connaissances de base sont représentées par la distribution a priori, qui est ensuite comparée et étudiée avec les données observées ou collectées en tant que fonction de vraisemblance pour déterminer la distribution a posteriori.

Cette distribution a posteriori est utilisée pour faire des prédictions sur des événements futurs.

Les applications de l'approche bayésienne dépendent des paramètres suivants :

1. Définition de l'a priori et du modèle de données
2. Faire des déductions pertinentes
3. Examen et rationalisation des modèles

Que sont les réseaux de neurones bayésiens ?

Les réseaux de neurones bayésiens (BNN) sont des réseaux que vous créez lorsque vous étendez des réseaux standard à l'aide de la méthodologie statistique et que vous modifiez l'inférence postérieure pour suivre le surajustement. S'agissant d'une approche bayésienne, il existe une distribution de probabilité associée aux paramètres des réseaux de neurones.

Ils sont utilisés pour résoudre des problèmes complexes où il n'y a pas un flux libre de données disponibles. Les réseaux de neurones bayésiens aident à contrôler le surajustement dans des domaines tels que la biologie moléculaire et le diagnostic médical.

On peut envisager toute une distribution de réponses à une question plutôt qu'une seule possibilité en utilisant les réseaux de neurones bayésiens. Ils vous aident à déterminer la sélection/comparaison de modèles et à résoudre les problèmes impliquant la régularisation.

Les statistiques bayésiennes offrent des outils mathématiques pour rationaliser et mettre à jour les connaissances subjectives concernant de nouvelles données ou preuves scientifiques. Contrairement à l'approche statistique fréquente, elle fonctionne sur la base de l'hypothèse que les probabilités dépendent de la fréquence des événements se répétant dans les mêmes conditions.

En bref, la technique bayésienne est une extension de l'hypothèse et de l'opinion d'un individu. L'aspect clé du modèle bayésien qui le rend plus efficace est sa compréhension que les individus diffèrent dans leurs opinions en fonction du type d'informations qu'ils reçoivent.

Cependant, à mesure que de nouvelles preuves et données apparaissent, les individus ont un point de convergence, l' inférence bayésienne . Cette mise à jour rationnelle est la particularité de la statistique bayésienne qui la rend plus efficace sur des problèmes analytiques.

Ici, la probabilité de 0 est appliquée lorsqu'il n'y a aucun espoir qu'un événement se produise, et la probabilité de 1 est appliquée lorsqu'il est certain que l'événement se produira. Une probabilité entre 0 et 1 laisse place à d'autres résultats potentiels.

La règle de Bayes est maintenant appliquée pour obtenir une inférence bayésienne afin d'obtenir une meilleure inférence à partir du modèle.

Comment appliquer la règle de Bayes pour obtenir une inférence bayésienne ?

Considérez l'équation:

P(θ|D) = P(D|θ.)P(θ) / P(D)

P(θ) désigne la distribution a priori,

P(θ|D) désigne la croyance a posteriori,

P(D) représente la preuve,

P(D|θ) indique la vraisemblance.

L'objectif principal de l'inférence bayésienne est d'offrir une méthode rationnelle et mathématiquement précise pour mélanger les croyances avec des preuves afin d'obtenir des croyances postérieures mises à jour. Les croyances a posteriori peuvent être utilisées comme croyances a priori lorsque de nouvelles données sont générées. Ainsi, l'inférence bayésienne aide à mettre à jour les croyances en continu à l'aide de la règle de Bayes.

En considérant le même exemple de pile ou face, le modèle bayésien met à jour la procédure des croyances antérieures aux croyances postérieures avec de nouveaux pile ou face. La méthode bayésienne donne les probabilités suivantes.

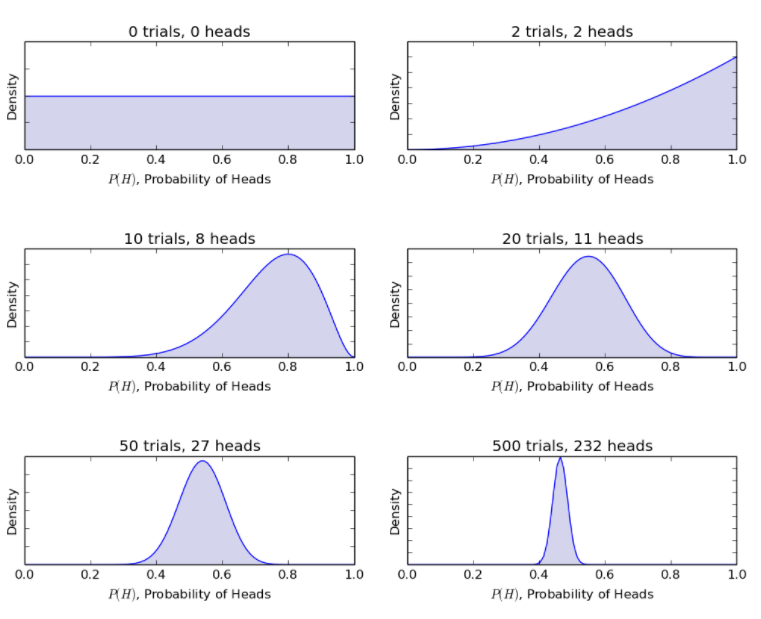
La source

Ainsi, le modèle bayésien permet de rationaliser un scénario incertain avec des informations restreintes vers un scénario plus défini avec une quantité considérable de données.

Différences notables entre le modèle bayésien et le modèle fréquentiste

Statistiques fréquentes

Statistiques bayésiennes

L'objectif est considéré comme une estimation ponctuelle, et CI

Le but est considéré comme une distribution a posteriori

La procédure part des observations

Le processus commence à partir de la distribution précédente

Chaque fois que de nouvelles observations sont faites, l'approche fréquentiste recalcule le modèle existant.

Chaque fois que de nouvelles observations sont faites, la distribution a posteriori (idéologie/hypothèse) est mise à jour

Exemples : Estimation de la moyenne, du test t et de l'ANOVA.

Exemples : Estimation de la distribution a posteriori de la moyenne et du chevauchement des intervalles de haute densité.

Avantages des statistiques bayésiennes

• Il fournit un moyen organique et simple de mélanger des informations préconçues avec un cadre solide avec des preuves scientifiques. Les informations passées sur un paramètre peuvent être utilisées pour former une distribution antérieure pour une enquête future. Les inférences respectent le théorème de Bayes.
• Les inférences d'un modèle bayésien sont des hypothèses logiques et mathématiquement exactes et non grossières. La précision reste constante quelle que soit la taille de l'échantillon.
• Les statistiques bayésiennes suivent le principe de vraisemblance. Lorsque deux échantillons différents ont une fonction de vraisemblance commune pour une croyance θ, toutes les inférences sur la croyance doivent être similaires. Les techniques statistiques classiques ne suivent pas le principe de vraisemblance.
• Les solutions d'une analyse bayésienne peuvent être facilement interprétées.
• Il offre une plate-forme propice à divers modèles tels que les modèles hiérarchiques et les problèmes de données incomplètes. Les calculs de tous les modèles paramétriques peuvent être suivis virtuellement à l'aide d'autres techniques numériques.

Applications réussies des modèles bayésiens à travers l'histoire

Les méthodes bayésiennes ont eu de nombreuses applications réussies pendant la Seconde Guerre mondiale. Quelques-uns d'entre eux sont énumérés ci-dessous :

• Un statisticien russe, Andrey Kolmogorov , a utilisé avec succès les méthodes bayésiennes pour améliorer l'efficacité de l'artillerie russe.
• Des modèles bayésiens ont été utilisés pour casser les codes des sous-marins allemands.
• Un mathématicien américain d'origine française, Bernard Koopman, a aidé les alliés à identifier l'emplacement des sous-marins allemands à l'aide de modèles bayésiens pour intercepter les transmissions radio.

Si vous souhaitez en savoir plus sur les statistiques bayésiennes, voici la certification avancée d'upGrad en apprentissage automatique et cloud pour comprendre les concepts sous-jacents à travers des projets industriels et des études de cas réels. Le cours de 12 mois est proposé par l'IIT Madras et prend en charge l'apprentissage à son rythme.

Contactez-nous pour plus de détails.