Exemple de réseau bayésien [avec représentation graphique]

introduction

En statistique, les modèles probabilistes sont utilisés pour définir une relation entre des variables et peuvent être utilisés pour calculer les probabilités de chaque variable. Dans de nombreux problèmes, il existe un grand nombre de variables. Dans de tels cas, les modèles entièrement conditionnels nécessitent une énorme quantité de données pour couvrir chaque cas des fonctions de probabilité qui peuvent être difficiles à calculer en temps réel. Il y a eu plusieurs tentatives pour simplifier les calculs de probabilité conditionnelle tels que le Naive Bayes, mais cela ne s'est toujours pas avéré efficace car il réduit considérablement plusieurs variables.

La seule façon est de développer un modèle qui peut préserver les dépendances conditionnelles entre les variables aléatoires et l'indépendance conditionnelle dans d'autres cas. Cela nous amène au concept de réseaux bayésiens. Ces réseaux bayésiens nous aident à visualiser efficacement le modèle probabiliste pour chaque domaine et à étudier la relation entre les variables aléatoires sous la forme d'un graphique convivial.

Apprenez le cours ML des meilleures universités du monde. Gagnez des programmes de maîtrise, Executive PGP ou Advanced Certificate pour accélérer votre carrière.

Que sont les réseaux bayésiens ?

Par définition, les réseaux bayésiens sont un type de modèle graphique probabiliste qui utilise les inférences bayésiennes pour les calculs de probabilité. Il représente un ensemble de variables et ses probabilités conditionnelles avec un graphe acyclique dirigé (DAG). Ils sont principalement adaptés pour considérer un événement qui s'est produit et prédire la probabilité que l'une des nombreuses causes connues possibles soit le facteur contributif.

La source

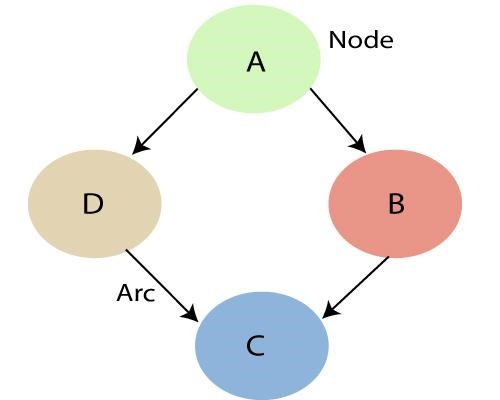
Comme mentionné ci-dessus, en utilisant les relations spécifiées par le réseau bayésien, nous pouvons obtenir la distribution de probabilité conjointe (JPF) avec les probabilités conditionnelles. Chaque nœud du graphique représente une variable aléatoire et l'arc (ou flèche dirigée) représente la relation entre les nœuds. Ils peuvent être de nature continue ou discrète.

Dans le diagramme ci-dessus A, B, C et D sont 4 variables aléatoires représentées par des nœuds donnés dans le réseau du graphe. Pour le nœud B, A est son nœud parent et C est son nœud enfant. Le nœud C est indépendant du nœud A.

Avant d'entrer dans la mise en œuvre d'un réseau bayésien, il y a quelques bases de probabilité qui doivent être comprises.

Propriété de Markov locale

Les réseaux bayésiens satisfont la propriété connue sous le nom de propriété de Markov locale. Il stipule qu'un nœud est conditionnellement indépendant de ses non-descendants, compte tenu de ses parents. Dans l'exemple ci-dessus, P(D|A, B) est égal à P(D|A) car D est indépendant de son non-descendant, B. Cette propriété nous aide à simplifier la distribution conjointe. La propriété de Markov locale nous amène au concept de champ aléatoire de Markov qui est un champ aléatoire autour d'une variable censée suivre les propriétés de Markov.

Probabilite conditionnelle

En mathématiques, la probabilité conditionnelle de l'événement A est la probabilité que l'événement A se produise étant donné qu'un autre événement B s'est déjà produit. En termes simples, p(A | B) est la probabilité que l'événement A se produise, étant donné que l'événement B se produit. Cependant, il existe deux types de possibilités d'événements entre A et B. Il peut s'agir soit d'événements dépendants, soit d'événements indépendants. Selon leur type, il existe deux manières différentes de calculer la probabilité conditionnelle.

• Étant donné que A et B sont des événements dépendants, la probabilité conditionnelle est calculée comme P (A | B) = P (A et B) / P (B)
• Si A et B sont des événements indépendants, alors l'expression de la probabilité conditionnelle est donnée par, P(A| B) = P (A)

Distribution de probabilité conjointe

Avant d'aborder un exemple de réseaux bayésiens, comprenons le concept de distribution de probabilité conjointe. Considérons 3 variables a1, a2 et a3. Par définition, les probabilités de toutes les différentes combinaisons possibles de a1, a2 et a3 sont appelées sa distribution de probabilité conjointe.

Si P[a1,a2, a3,….., an] est le JPD des variables suivantes de a1 à an, alors il existe plusieurs façons de calculer la distribution de probabilité conjointe comme une combinaison de divers termes tels que,

P[a1,a2, a3,….., an] = P[a1 | a2, a3,….., une] * P[a2, a3,….., une]

= P[a1 | a2, a3,….., an] * P[a2 | a3,….., une]….P[an-1|an] * P[an]

En généralisant l'équation ci-dessus, nous pouvons écrire la distribution de probabilité conjointe comme suit :

P(X je |X je-1 ,………, X n ) = P(X je |Parents(X je ))

Exemple de réseaux bayésiens

Comprenons maintenant le mécanisme des Réseaux Bayésiens et leurs avantages à l'aide d'un exemple simple. Dans cet exemple, imaginons que l'on nous confie la tâche de modéliser les notes ( m ) d'un élève pour un examen qu'il vient de passer. À partir du graphique de réseau bayésien ci-dessous, nous voyons que les notes dépendent de deux autres variables. Elles sont,

• Niveau d'examen ( e )– Cette variable discrète indique la difficulté de l'examen et a deux valeurs (0 pour facile et 1 pour difficile)
• Niveau de QI ( i ) - Cela représente le niveau de quotient intellectuel de l'élève et est également de nature discrète avec deux valeurs (0 pour bas et 1 pour haut)

De plus, le niveau de QI de l'élève nous amène également à une autre variable, qui est le score d'aptitude de l'élève ( s ). Maintenant, avec les notes que l'étudiant a obtenues, il peut être admis dans une université particulière. La distribution de probabilité d'être admis ( a ) dans une université est également donnée ci-dessous.

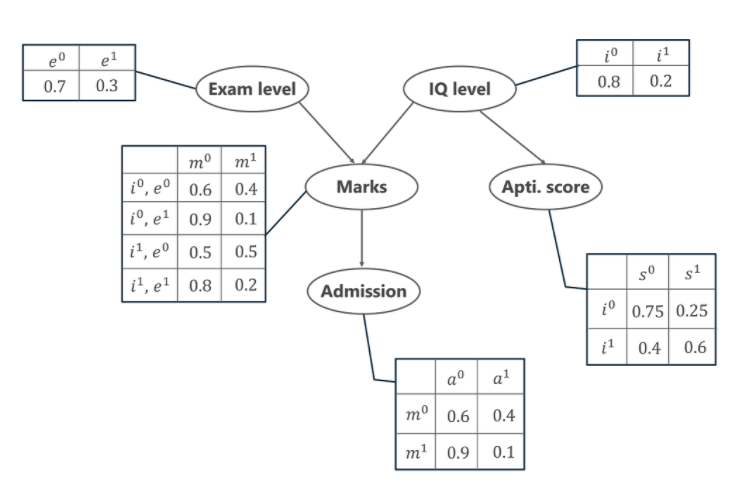
Dans le graphique ci-dessus, nous voyons plusieurs tableaux représentant les valeurs de distribution de probabilité des 5 variables données. Ces tables sont appelées table de probabilités conditionnelles ou CPT. Il y a quelques propriétés du CPT données ci-dessous -

• La somme des valeurs CPT dans chaque ligne doit être égale à 1 car tous les cas possibles pour une variable particulière sont exhaustifs (représentant toutes les possibilités).
• Si une variable de nature booléenne a k parents booléens, alors dans le CPT, elle a 2K valeurs de probabilité.

Pour en revenir à notre problème, énumérons d'abord tous les événements possibles qui se produisent dans le tableau ci-dessus.

1. Niveau d'examen (e)
2. Niveau de QI (i)
3. Note(s) d'aptitude
4. Marques (m)
5. Entrée (a)

Ces cinq variables sont représentées sous la forme d'un graphe acyclique dirigé (DAG) dans un format de réseau bayésien avec leurs tables de probabilités conditionnelles. Maintenant, pour calculer la distribution de probabilité conjointe des 5 variables, la formule est donnée par,

P[a, m, je, e, s]= P(a | m) . P(m | je, e) . P(i) . P(e) . P(s | je)

De la formule ci-dessus,

• P(a | m) désigne la probabilité conditionnelle que l'étudiant soit admis en fonction des notes qu'il a obtenues à l'examen.
• P(m | i, e) représente les notes que l'étudiant obtiendra compte tenu de son niveau de QI et de la difficulté du niveau d'examen.
• P(i) et P(e) représentent la probabilité du niveau de QI et du niveau d'examen.
• P(s | i) est la probabilité conditionnelle du score d'aptitude de l'élève, compte tenu de son niveau de QI.

Avec les probabilités suivantes calculées, nous pouvons trouver la distribution de probabilité conjointe de l'ensemble du réseau bayésien.

Calcul de la distribution de probabilité conjointe

Calculons maintenant le JPD pour deux cas.

Cas 1 : Calculez la probabilité que, malgré le niveau d'examen difficile, l'étudiant ayant un faible niveau de QI et un faible score d'aptitude, réussisse l'examen et soit admis à l'université.

À partir de l'énoncé du problème de mot ci-dessus, la distribution de probabilité conjointe peut être écrite comme ci-dessous,

P[a=1, m=1, i=0, e=1, s=0]

À partir des tables de probabilité conditionnelle ci-dessus, les valeurs des conditions données sont introduites dans la formule et sont calculées comme ci-dessous.

P[a=1, m=1, i=0, e=0, s=0] = P(a=1 | m=1) . P(m=1 | je=0, e=1) . P(i=0) . P(e=1) . P(s=0 | je=0)

= 0,1 * 0,1 * 0,8 * 0,3 * 0,75

= 0,0018

Cas 2 : Dans un autre cas, calculez la probabilité que l'étudiant ait un niveau de QI et un score d'aptitude élevés, l'examen étant facile mais ne réussissant pas et ne garantissant pas l'admission à l'université.

La formule du JPD est donnée par

P[a=0, m=0, i=1, e=0, s=1]

Ainsi,

P[a=0, m=0, i=1, e=0, s=1]= P(a=0 | m=0) . P(m=0 | je=1, e=0) . P(i=1) . P(e=0) . P(s=1 | je=1)

= 0,6 * 0,5 * 0,2 * 0,7 * 0,6

= 0,0252

Par conséquent, de cette manière, nous pouvons utiliser les réseaux bayésiens et les tables de probabilité pour calculer la probabilité de divers événements possibles qui se produisent.

Lisez aussi : Idées et sujets de projets d'apprentissage automatique

Conclusion

Il existe d'innombrables applications aux réseaux bayésiens dans le filtrage anti-spam, la recherche sémantique, la récupération d'informations et bien d'autres. Par exemple, avec un symptôme donné, nous pouvons prédire la probabilité qu'une maladie survienne avec plusieurs autres facteurs contribuant à la maladie. Ainsi, le concept de réseau bayésien est présenté dans cet article ainsi que sa mise en œuvre avec un exemple concret.

Si vous êtes curieux de maîtriser l'apprentissage automatique et l'IA, dynamisez votre carrière avec un cours avancé sur l'apprentissage automatique et l'IA avec l'IIIT-B et l'Université John Moores de Liverpool.