Théorème de Bayes dans l'apprentissage automatique : introduction, application et exemple
Publié: 2021-02-04Table des matières
Introduction : qu'est-ce que le théorème de Bayes ?
Le théorème de Bayes porte le nom du mathématicien anglais Thomas Bayes, qui a beaucoup travaillé sur la théorie de la décision, le domaine des mathématiques qui implique des probabilités. Le théorème de Bayes est également largement utilisé dans l'apprentissage automatique, où il s'agit d'un moyen simple et efficace de prédire les classes avec précision et exactitude. La méthode bayésienne de calcul des probabilités conditionnelles est utilisée dans les applications d'apprentissage automatique qui impliquent des tâches de classification.
Une version simplifiée du théorème de Bayes, connue sous le nom de classification naïve de Bayes, est utilisée pour réduire le temps et les coûts de calcul. Dans cet article, nous vous présentons ces concepts et discutons des applications du théorème de Bayes dans l'apprentissage automatique.
Rejoignez le cours d'apprentissage automatique en ligne des meilleures universités du monde - Masters, Executive Post Graduate Programs et Advanced Certificate Program in ML & AI pour accélérer votre carrière.
Pourquoi utiliser le théorème de Bayes en Machine Learning ?
Le théorème de Bayes est une méthode pour déterminer les probabilités conditionnelles, c'est-à-dire la probabilité qu'un événement se produise étant donné qu'un autre événement s'est déjà produit. Parce qu'une probabilité conditionnelle inclut des conditions supplémentaires - en d'autres termes, plus de données - elle peut contribuer à des résultats plus précis.
Ainsi, les probabilités conditionnelles sont indispensables pour déterminer des prédictions et des probabilités précises dans l'apprentissage automatique. Étant donné que le domaine devient de plus en plus omniprésent dans une variété de domaines, il est important de comprendre le rôle des algorithmes et des méthodes comme le théorème de Bayes dans l'apprentissage automatique.
Avant d'entrer dans le théorème lui-même, comprenons quelques termes à travers un exemple. Supposons qu'un libraire dispose d'informations sur l'âge et les revenus de ses clients. Il veut savoir comment les ventes de livres sont réparties entre trois tranches d'âge de clients : les jeunes (18-35), les personnes d'âge moyen (35-60) et les seniors (60+).

Appelons nos données X. Dans la terminologie bayésienne, X est appelé preuve. Nous avons une hypothèse H, où nous avons un certain X qui appartient à une certaine classe C.
Notre but est de déterminer la probabilité conditionnelle de notre hypothèse H étant donné X, c'est-à-dire P(H | X).
En termes simples, en déterminant P(H | X), nous obtenons la probabilité que X appartienne à la classe C, étant donné X. X a des attributs d'âge et de revenu - disons, par exemple, 26 ans avec un revenu de 2 000 $. H est notre hypothèse que le client achètera le livre.
Portez une attention particulière aux quatre termes suivants :
- Preuve - Comme indiqué précédemment, P (X) est connu comme preuve. Il s'agit simplement de la probabilité que le client soit, dans ce cas, âgé de 26 ans et gagne 2 000 $.
- Probabilité a priori - P(H), connue sous le nom de probabilité a priori, est la probabilité simple de notre hypothèse, à savoir que le client achètera un livre. Cette probabilité ne sera pas fournie avec une entrée supplémentaire basée sur l'âge et le revenu. Étant donné que le calcul est effectué avec moins d'informations, le résultat est moins précis.
- Probabilité postérieure - P (H | X) est connue sous le nom de probabilité postérieure. Ici, P(H | X) est la probabilité que le client achète un livre (H) étant donné X (qu'il ait 26 ans et gagne 2 000 $).
- Probabilité – P(X | H) est la probabilité de vraisemblance. Dans ce cas, étant donné que nous savons que le client achètera le livre, la probabilité de vraisemblance est la probabilité que le client ait 26 ans et ait un revenu de 2 000 $.
Compte tenu de ceux-ci, le théorème de Bayes déclare:
P(H | X) = [ P(X | H) * P(H) ] / P(X)
Notez l'apparition des quatre termes ci-dessus dans le théorème - probabilité postérieure, probabilité de vraisemblance, probabilité antérieure et preuve.
Lire : Bayes naïf expliqué
Comment appliquer le théorème de Bayes dans l'apprentissage automatique
Le classificateur Naive Bayes, une version simplifiée du théorème de Bayes, est utilisé comme algorithme de classification pour classer les données en différentes classes avec précision et rapidité.
Voyons comment le Naive Bayes Classifier peut être appliqué comme algorithme de classification.
- Prenons un exemple général : X est un vecteur constitué de 'n' attributs, c'est-à-dire X = {x1, x2, x3, …, xn}.
- Supposons que nous ayons 'm' classes {C1, C2, …, Cm}. Notre classificateur devra prédire que X appartient à une certaine classe. La classe offrant la probabilité a posteriori la plus élevée sera choisie comme la meilleure classe. Donc mathématiquement, le classificateur prédira pour la classe Ci ssi P(Ci | X) > P(Cj | X). Application du théorème de Bayes :
P(Ci | X) = [ P(X | Ci) * P(Ci) ] / P(X)
- P(X), étant indépendant de la condition, est constant pour chaque classe. Donc pour maximiser P(Ci | X), il faut maximiser [P(X | Ci) * P(Ci)]. Considérant que chaque classe est également probable, nous avons P(C1) = P(C2) = P(C3) … = P(Cn). Donc, en fin de compte, nous devons maximiser uniquement P(X | Ci).
- Étant donné que le grand ensemble de données typique est susceptible d'avoir plusieurs attributs, il est coûteux en calcul d'effectuer l'opération P(X | Ci) pour chaque attribut. C'est là qu'intervient l'indépendance conditionnelle de classe pour simplifier le problème et réduire les coûts de calcul. Par indépendance conditionnelle de classe, nous entendons que nous considérons que les valeurs de l'attribut sont conditionnellement indépendantes les unes des autres. C'est la classification naïve de Bayes.
P(Xi | C) = P(x1 | C) * P(x2 | C) *… * P(xn | C)
Il est maintenant facile de calculer les plus petites probabilités. Une chose importante à noter ici : puisque xk appartient à chaque attribut, nous devons également vérifier si l'attribut dont nous parlons est catégorique ou continu .
- Si nous avons un attribut catégoriel , les choses sont plus simples. Nous pouvons simplement compter le nombre d'instances de la classe Ci consistant en la valeur xk pour l'attribut k, puis diviser cela par le nombre d'instances de la classe Ci.
- Si nous avons un attribut continu, considérant que nous avons une fonction de distribution normale, nous appliquons la formule suivante, avec une moyenne ? et écart-type ? :
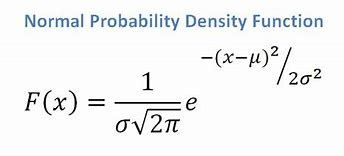

La source
Au final, on aura P(x | Ci) = F(xk, ?k, ?k).
- Maintenant, nous avons toutes les valeurs dont nous avons besoin pour utiliser le théorème de Bayes pour chaque classe Ci. Notre classe prédite sera la classe obtenant la probabilité la plus élevée P(X | Ci) * P(Ci).
Exemple : Classification prédictive des clients d'une librairie
Nous avons l'ensemble de données suivant d'une librairie :
| Âge | Revenu | Élève | Credit_Rating | Achats_Livre |
| Jeunesse | Haut | Non | Équitable | Non |
| Jeunesse | Haut | Non | Excellent | Non |
| Âge moyen | Haut | Non | Équitable | Oui |
| Sénior | Moyen | Non | Équitable | Oui |
| Sénior | Meugler | Oui | Équitable | Oui |
| Sénior | Meugler | Oui | Excellent | Non |
| Âge moyen | Meugler | Oui | Excellent | Oui |
| Jeunesse | Moyen | Non | Équitable | Non |
| Jeunesse | Meugler | Oui | Équitable | Oui |
| Sénior | Moyen | Oui | Équitable | Oui |
| Jeunesse | Moyen | Oui | Excellent | Oui |
| Âge moyen | Moyen | Non | Excellent | Oui |
| Âge moyen | Haut | Oui | Équitable | Oui |
| Sénior | Moyen | Non | Excellent | Non |
Nous avons des attributs comme l'âge, le revenu, l'étudiant et la cote de crédit. Notre classe, buys_book, a deux résultats : Oui ou Non.
Notre objectif est de classer en fonction des attributs suivants :
X = {âge = jeune, étudiant = oui, revenu = moyen, cote de crédit = juste}.
Comme nous l'avons montré précédemment, pour maximiser P(Ci | X), nous devons maximiser [ P(X | Ci) * P(Ci) ] pour i = 1 et i = 2.
Par conséquent, P(buys_book = yes) = 9/14 = 0,643
P(buys_book = non) = 5/14 = 0,357
P(âge = jeune | achète_livre = oui) = 2/9 = 0,222
P(âge = jeune | achète_livre = non) =3/5 = 0,600
P(revenu = moyen | achat_livre = oui) = 4/9 = 0,444
P(revenu = moyen | achat_livre = non) = 2/5 = 0,400
P(étudiant = oui | achète_livre = oui) = 6/9 = 0,667
P(étudiant = oui | achète_livre = non) = 1/5 = 0,200
P(credit_rating = fair | buys_book = yes) = 6/9 = 0,667
P(credit_rating = fair | buys_book = no) = 2/5 = 0,400
En utilisant les probabilités calculées ci-dessus, nous avons
P(X | achète_livre = oui) = 0,222 x 0,444 x 0,667 x 0,667 = 0,044
De même,
P(X | achète_livre = non) = 0,600 x 0,400 x 0,200 x 0,400 = 0,019
Quelle classe Ci fournit le maximum P(X|Ci)*P(Ci) ? Nous calculons :
P(X | buys_book = yes)* P(buys_book = yes) = 0,044 x 0,643 = 0,028
P(X | achat_livre = non)* P(achat_livre = non) = 0,019 x 0,357 = 0,007

En comparant les deux ci-dessus, puisque 0,028 > 0,007, le classificateur Naive Bayes prédit que le client avec les attributs mentionnés ci-dessus achètera un livre.
Checkout : Idées et sujets de projets d'apprentissage automatique
Le classificateur bayésien est-il une bonne méthode ?
Les algorithmes basés sur le théorème de Bayes dans l'apprentissage automatique fournissent des résultats comparables à d'autres algorithmes, et les classificateurs bayésiens sont généralement considérés comme des méthodes simples de haute précision. Cependant, il faut veiller à se rappeler que les classificateurs bayésiens sont particulièrement appropriés lorsque l'hypothèse d'indépendance conditionnelle de classe est valide, et non dans tous les cas. Une autre préoccupation pratique est que l'acquisition de toutes les données de probabilité n'est pas toujours possible.
Conclusion
Le théorème de Bayes a de nombreuses applications en apprentissage automatique, en particulier dans les problèmes basés sur la classification. L'application de cette famille d'algorithmes dans l'apprentissage automatique implique de se familiariser avec des termes tels que probabilité a priori et probabilité a posteriori. Dans cet article, nous avons abordé les bases du théorème de Bayes, son utilisation dans les problèmes d'apprentissage automatique et travaillé sur un exemple de classification.
Étant donné que le théorème de Bayes constitue un élément crucial des algorithmes basés sur la classification dans l'apprentissage automatique, vous pouvez en savoir plus sur le programme de certificat avancé d'upGrad en apprentissage automatique et en PNL . Ce cours a été conçu en gardant à l'esprit différents types d'étudiants intéressés par l'apprentissage automatique, offrant un mentorat 1-1 et bien plus encore.
Pourquoi utilisons-nous le théorème de Bayes en Machine Learning ?
Le théorème de Bayes est une méthode de calcul des probabilités conditionnelles, ou la probabilité qu'un événement se produise si un autre s'est déjà produit. Une probabilité conditionnelle peut conduire à des résultats plus précis en incluant des conditions supplémentaires - en d'autres termes, plus de données. Afin d'obtenir des estimations et des probabilités correctes en Machine Learning, des probabilités conditionnelles sont nécessaires. Compte tenu de la prévalence croissante du domaine dans un large éventail de domaines, il est essentiel de comprendre l'importance des algorithmes et des approches comme le théorème de Bayes dans l'apprentissage automatique.
Le classificateur bayésien est-il un bon choix ?
Dans l'apprentissage automatique, les algorithmes basés sur le théorème de Bayes produisent des résultats comparables à ceux d'autres méthodes, et les classificateurs bayésiens sont largement considérés comme de simples approches de haute précision. Cependant, il est important de garder à l'esprit que les classificateurs bayésiens sont mieux utilisés lorsque la condition d'indépendance conditionnelle de classe est correcte, et non dans toutes les circonstances. Une autre considération est qu'il n'est pas toujours possible d'obtenir toutes les données de probabilité.
Comment appliquer concrètement le théorème de Bayes ?
Le théorème de Bayes calcule la probabilité d'occurrence sur la base de nouvelles preuves qui y sont ou pourraient y être liées. La méthode peut également être utilisée pour voir comment de nouvelles informations hypothétiques affectent la probabilité d'un événement, en supposant que les nouvelles informations sont vraies. Prenez, par exemple, une seule carte choisie parmi un jeu de 52 cartes. La probabilité que la carte devienne un roi est de 4 divisé par 52, soit 1/13, soit environ 7,69 %. Gardez à l'esprit que le jeu contient quatre rois. Disons qu'il est révélé que la carte choisie est une figure. Parce qu'il y a 12 cartes faciales dans un jeu, la probabilité que la carte choisie soit un roi est de 4 divisé par 12, soit environ 33,3 %.
