Théorème de Bayes expliqué avec un exemple - Guide complet

introduction

Qu'est-ce que le théorème de Bayes ?

Le théorème de Bayes est utilisé pour le calcul d'une probabilité conditionnelle où l'intuition échoue souvent. Bien que largement utilisé en probabilité, le théorème est également appliqué dans le domaine de l'apprentissage automatique. Son utilisation dans l'apprentissage automatique comprend l'ajustement d'un modèle à un ensemble de données de formation et le développement de modèles de classification.

Qu'est-ce que la probabilité conditionnelle ?

Une probabilité conditionnelle est généralement définie comme la probabilité d'un événement compte tenu de l'occurrence d'un autre événement.

• Si A et B sont deux événements, alors la probabilité conditionnelle peut être désignée par P(A étant donné B) ou P(A|B).
• La probabilité conditionnelle peut être calculée à partir de la probabilité conjointe (A | B) = P(A, B) / P(B)

• La probabilité conditionnelle n'est pas symétrique ; Par exemple P(A | B) != P(B | A)

D'autres façons de calculer la probabilité conditionnelle incluent l'utilisation de l'autre probabilité conditionnelle, c'est-à-dire

P(A|B) = P(B|A) * P(A) / P(B)

L'inverse est également utilisé

P(B|A) = P(A|B) * P(B) / P(A)

Cette méthode de calcul est utile lorsqu'il est difficile de calculer la probabilité conjointe. Sinon, lorsque la probabilité conditionnelle inverse est disponible, le calcul via celle-ci devient facile.

Ce calcul alternatif de probabilité conditionnelle est appelé règle de Bayes ou théorème de Bayes. Il porte le nom de la personne qui l'a décrit pour la première fois, « le révérend Thomas Bayes ».

La formule du théorème de Bayes

Le théorème de Bayes est un moyen de calculer la probabilité conditionnelle lorsque la probabilité conjointe n'est pas disponible. Parfois, le dénominateur n'est pas directement accessible. Dans de tels cas, la méthode alternative de calcul est la suivante :

P(B) = P(B|A) * P(A) + P(B|pas A) * P(pas A)

C'est la formulation du théorème de Bayes qui montre un autre calcul de P(B).

P(A|B) = P(B|A) * P(A) / P(B|A) * P(A) + P(B|pas A) * P(pas A)

La formule ci-dessus peut être décrite avec des parenthèses autour du dénominateur

P(A|B) = P(B|A) * P(A) / (P(B|A) * P(A) + P(B|pas A) * P(pas A))

De plus, si nous avons P (A), alors le P (non A) peut être calculé comme

P(non A) = 1 – P(A)

De même, si nous avons P(not B|not A), alors P(B|not A) peut être calculé comme

P(B|non A) = 1 – P(non B|non A)

Théorème de probabilité conditionnelle de Bayes

Le théorème de Bayes se compose de plusieurs termes dont les noms sont donnés en fonction du contexte de son application dans l'équation.

La probabilité postérieure fait référence au résultat de P(A|B) et la probabilité a priori fait référence à P(A).

• P(A|B) : Probabilité a posteriori.
• P(A) : Probabilité a priori.

De même, P(B|A) et P(B) sont appelés la probabilité et la preuve.

• P(B|A) : Probabilité.
• P(B) : Preuve.

Par conséquent, le théorème de Bayes de la probabilité conditionnelle peut être reformulé comme suit :

Postérieure = Probabilité * Antérieure / Preuve

Si nous devons calculer la probabilité qu'il y ait du feu étant donné qu'il y a de la fumée, alors l'équation suivante sera utilisée :

P(Feu|Fumée) = P(Fumée|Feu) * P(Feu) / P(Fumée)

Où, P(Feu) est le Prieur, P(Fumée|Feu) est la Probabilité, et P(Fumée) est la preuve.

Une illustration du théorème de Bayes

Un exemple de théorème de Bayes est décrit pour illustrer l'utilisation du théorème de Bayes dans un problème.

Problème

Trois cases étiquetées A, B et C sont présentes. Les détails des boîtes sont :

• La boîte A contient 2 boules rouges et 3 boules noires
• La boîte B contient 3 boules rouges et 1 boule noire
• Et la case C contient 1 boule rouge et 4 boules noires

Les trois cases sont identiques et ont une probabilité égale d'être ramassées. Quelle est donc la probabilité que la bille rouge ait été récupérée dans la case A ?

Solution

Soit E l'événement où une balle rouge est ramassée et A, B et C indiquent que la balle est ramassée dans leurs cases respectives. Par conséquent, la probabilité conditionnelle serait P(A|E) qui doit être calculée.

Les probabilités existantes P(A) = P(B) = P (C) = 1 / 3, puisque toutes les cases ont la même probabilité d'être sélectionnées.

P(E|A) = Nombre de billes rouges dans la case A / Nombre total de billes dans la case A = 2 / 5

De même, P(E|B) = 3 / 4 et P(E|C) = 1 / 5

Alors preuve P(E) = P(E|A)*P(A) + P(E|B)*P(B) + P(E|C)*P(C)

= (2/5) * (1/3) + (3/4) * (1/3) + (1/5) * (1/3) = 0,45

Par conséquent, P(A|E) = P(E|A) * P(A) / P(E) = (2/5) * (1/3) / 0,45 = 0,296

Exemple de théorème de Bayes

Le théorème de Bayes donne la probabilité d'un "événement" avec les informations données sur les "tests".

• Il y a une différence entre « événements » et « tests ». Par exemple, il existe un test pour une maladie du foie, qui est différent d'avoir réellement la maladie du foie, c'est-à-dire un événement.
• Les événements rares peuvent avoir un taux de faux positifs plus élevé.

Exemple 1

Quelle est la probabilité qu'un patient ait une maladie du foie s'il est alcoolique ?

Ici, « être alcoolique » est le « test » (type de test décisif) pour une maladie du foie.

• A est l'événement, c'est-à-dire « le patient a une maladie du foie » ».

Selon les enregistrements antérieurs de la clinique, il est indiqué que 10% des patients entrant dans la clinique souffrent d'une maladie du foie.

Par conséquent, P(A)=0,10

• B est le test décisif que "le patient est un alcoolique".

Les dossiers antérieurs de la clinique ont montré que 5% des patients entrant dans la clinique sont alcooliques.

Par conséquent, P(B)=0,05

• En outre, 7% des patients chez qui on a diagnostiqué une maladie du foie sont des alcooliques. Ceci définit le B|A : la probabilité qu'un patient soit alcoolique, sachant qu'il a une maladie du foie est de 7 %.

Selon la formule du théorème de Bayes ,

P(A|B) = (0,07 * 0,1)/0,05 = 0,14

Ainsi, pour un patient alcoolique, les chances d'avoir une maladie du foie sont de 0,14 (14%).

Exemple2

• Les incendies dangereux sont rares (1%)
• Mais la fumée est assez courante (10%) à cause des barbecues,
• Et 90% des incendies dangereux produisent de la fumée

Quelle est la probabilité d'incendie dangereux lorsqu'il y a de la fumée ?

Calcul

P(Feu|Fumée) =P(Feu) P(Fumée|Feu)/P(Fumée)

= 1 % × 90 %/10 %

= 9%

Exemple 3

Quel est le risque de pluie pendant la journée ? Où, Rain signifie pluie pendant la journée, et Cloud signifie matin nuageux.

La chance de Pluie étant donnée Cloud s'écrit P(Rain|Cloud)

P(Pluie|Nuage) = P(Pluie) P(Nuage|Pluie)/P(Nuage)

P(pluie) est la probabilité de pluie = 10 %

P(Cloud|Rain) est la probabilité de Cloud, étant donné que la pluie se produit = 50 %

P(Cloud) est la probabilité de Cloud = 40 %

P(Pluie|Nuage) = 0,1 x 0,5/0,4 = 0,125

Par conséquent, 12,5 % de chance de pluie.

Applications

Plusieurs applications du théorème de Bayes existent dans le monde réel. Les quelques applications principales du théorème sont :

1. Hypothèses de modélisation

Le théorème de Bayes trouve une large application dans l'apprentissage automatique appliqué et établit une relation entre les données et un modèle. L'apprentissage automatique appliqué utilise le processus de test et d'analyse de différentes hypothèses sur un ensemble de données donné.

Pour décrire la relation entre les données et le modèle, le théorème de Bayes fournit un modèle probabiliste.

P(h|D) = P(D|h) * P(h) / P(D)

Où,

P(h|D) : Probabilité a posteriori de l'hypothèse

P(h) : Probabilité a priori de l'hypothèse.

Une augmentation de P(D) diminue le P(h|D). Inversement, si P(h) et la probabilité d'observer les données données sous l'hypothèse augmentent, alors la probabilité de P(h|D) augmente.

2. Théorème de Bayes pour la classification

La méthode de classification implique l'étiquetage d'une donnée donnée. Il peut être défini comme le calcul de la probabilité conditionnelle d'une étiquette de classe compte tenu d'un échantillon de données.

P(classe|données) = (P(données|classe) * P(classe)) / P(données)

Où P(classe|données) est la probabilité de classe compte tenu des données fournies.

Le calcul peut être effectué pour chaque classe. La classe ayant la plus grande probabilité peut être affectée aux données d'entrée.

Le calcul de la probabilité conditionnelle n'est pas réalisable dans les conditions d'un petit nombre d'exemples. Par conséquent, l'application directe du théorème de Bayes n'est pas réalisable. Une solution au modèle de classification réside dans le calcul simplifié.

• Classificateur naïf de Bayes

Le théorème de Bayes considère que les variables d'entrée dépendent d'autres variables qui causent la complexité du calcul. Par conséquent, l'hypothèse est supprimée et chaque variable d'entrée est considérée comme une variable indépendante. En conséquence, le modèle passe d'un modèle de probabilité conditionnelle dépendant à indépendant. Cela réduit finalement la complexité.

Cette simplification du théorème de Bayes est appelée Bayes naïf. Il est largement utilisé pour les modèles de classification et de prédiction.

• Classificateur optimal de Bayes

Il s'agit d'un type de modèle probabiliste qui implique la prédiction d'un nouvel exemple compte tenu de l'ensemble de données d'apprentissage. Un exemple du classificateur optimal de Bayes est "Quelle est la classification la plus probable de la nouvelle instance compte tenu des données d'entraînement ?"

Le calcul de la probabilité conditionnelle d'une nouvelle instance compte tenu des données d'apprentissage peut être effectué à l'aide de l'équation suivante

P(vj | D) = somme {h dans H} P(vj | hi) * P(hi | D)

Où vj est une nouvelle instance à classer,

H est l'ensemble des hypothèses de classification de l'instance,

salut est une hypothèse donnée,

P(vj | hi) est la probabilité a posteriori pour vi étant donné l'hypothèse hi, et

P(hi | D) est la probabilité a posteriori de l'hypothèse hi compte tenu des données D.

3. Utilisations du théorème de Bayes en apprentissage automatique

L'application la plus courante du théorème de Bayes en apprentissage automatique est le développement de problèmes de classification. D'autres applications plutôt que la classification incluent l'optimisation et les modèles occasionnels.

• Optimisation bayésienne

Il est toujours difficile de trouver une entrée qui se traduit par le coût minimum ou maximum d'une fonction objectif donnée. L'optimisation bayésienne est basée sur le théorème de Bayes et fournit un aspect pour la recherche d'un problème d'optimisation global. Le procédé comprend la construction d'un modèle probabiliste (fonction de substitution), la recherche dans une fonction d'acquisition et la sélection d'échantillons candidats pour évaluer la fonction objectif réelle.

Dans l'apprentissage automatique appliqué, l'optimisation bayésienne est utilisée pour régler les hyperparamètres d'un modèle performant.

• Réseaux de croyances bayésiennes

Les relations entre les variables peuvent être définies à l'aide de modèles probabilistes. Ils sont également utilisés pour le calcul des probabilités. Un modèle de probabilité entièrement conditionnel peut ne pas être en mesure de calculer les probabilités en raison du grand volume de données. Naive Bayes a simplifié l'approche pour le calcul. Encore une autre méthode existe où un modèle est développé sur la base de la dépendance conditionnelle connue entre les variables aléatoires et l'indépendance conditionnelle dans d'autres cas. Le réseau bayésien affiche cette dépendance et cette indépendance à travers le modèle de graphe probabiliste avec des arêtes dirigées. La dépendance conditionnelle connue est affichée sous forme d'arêtes dirigées et les connexions manquantes représentent les indépendances conditionnelles dans le modèle.

4. Filtrage bayésien du spam

Le filtrage du spam est une autre application du théorème de Bayes. Deux événements sont présents :

• Événement A : Le message est un spam.
• Test X : Le message contient certains mots (X)

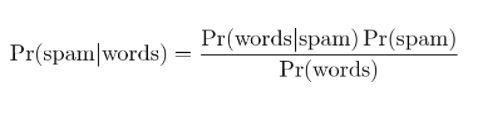
Avec l'application du théorème de Bayes, il est possible de prédire si le message est un spam compte tenu des « résultats du test ». L'analyse des mots d'un message peut calculer les chances qu'il s'agisse d'un message indésirable. Avec la formation de filtres avec des messages répétés, il met à jour le fait que la probabilité d'avoir certains mots dans le message serait du spam.

Une application du théorème de Bayes avec un exemple

Un producteur de catalyseur produit un appareil pour tester les défauts d'un certain électrocatalyseur (EC). Le producteur de catalyseur affirme que le test est fiable à 97 % si l'EC est défectueux et fiable à 99 % lorsqu'il est sans défaut. Cependant, on peut s'attendre à ce que 4 % dudit EC soient défectueux à la livraison. La règle de Bayes est appliquée pour déterminer la véritable fiabilité de l'appareil. Les ensembles d'événements de base sont

A : le CE est défectueux ; A' : le CE est sans faute ; B : l'EC est testé pour être défectueux ; B' : le CE est testé pour être irréprochable.

Les probabilités seraient

B/A : EC est (connu comme) défectueux, et testé défectueux, P(B/A) = 0,97,

B'/A : EC est (connu pour être) défectueux, mais testé sans défaut, P(B'/A)=1-P(B/A)=0,03,

B/A' : EC est (connu comme) défectueux, mais testé défectueux, P(B/A') = 1- P(B'/A')=0.01

B'/A : = EC est (connu pour être) sans défaut, et testé sans défaut P(B'/A') = 0,99

Les probabilités calculées par le théorème de Bayes sont :

La probabilité de calcul montre qu'il existe une forte possibilité de rejeter des EC sans défaut (environ 20 %) et une faible possibilité d'identifier des EC défectueux (environ 80 %).

Conclusion

L'une des caractéristiques les plus frappantes d'un théorème de Bayes est qu'à partir de quelques rapports de probabilité, une énorme quantité d'informations peut être obtenue. Avec les moyens de vraisemblance, la probabilité d'un événement antérieur peut être transformée en probabilité postérieure. Les approches du théorème de Bayes peuvent être appliquées dans les domaines de la statistique, de l'épistémologie et de la logique inductive.

Si vous souhaitez en savoir plus sur le théorème de Bayes, l'IA et l'apprentissage automatique, consultez le programme Executive PG d'IIIT-B & upGrad en apprentissage automatique et en IA, conçu pour les professionnels en activité et offrant plus de 450 heures de formation rigoureuse, plus de 30 cas études et missions, statut IIIT-B Alumni, plus de 5 projets de synthèse pratiques et aide à l'emploi avec les meilleures entreprises.