¿Qué es el pensamiento bayesiano? Introducción y Teorema

Un teorema estadístico propuesto por el estadístico y filósofo inglés Thomas Bayes en el siglo XVIII sigue siendo una luz de guía para científicos y analistas de todo el mundo. Hoy, el pensamiento bayesiano encuentra aplicación en la medicina, la ciencia, la tecnología y varias otras disciplinas y continúa influyendo fuertemente en nuestra visión del mundo y las acciones resultantes.

La idea de Thomas Bayes era sorprendentemente simple. Según Bayes, la probabilidad de que una hipótesis sea cierta depende de dos condiciones: qué tan razonable es en base a lo que ya sabemos (el conocimiento previo) y qué tan bien se ajusta a la nueva evidencia. Por lo tanto, el pensamiento bayesiano se diferencia de la prueba de hipótesis tradicional en que el primero incluye el conocimiento previo antes de sacar conclusiones precipitadas.

Con la introducción preliminar en mente, profundicemos un poco más sobre las estadísticas bayesianas.

Estadísticas bayesianas

En términos simples, las estadísticas bayesianas aplican probabilidades a problemas estadísticos para actualizar creencias previas a la luz de la evidencia de nuevos datos. La probabilidad expresa un grado de creencia en un evento específico.

El grado de creencia puede basarse en el conocimiento previo sobre el evento basado en suposiciones personales o resultados de experimentos anteriores. Las estadísticas bayesianas utilizan el teorema de Bayes para calcular probabilidades. El Teorema de Bayes, a su vez, describe la probabilidad condicional de un evento con base en nueva evidencia e información previa relacionada con el evento.

Con eso en mente, repasemos el concepto fundamental de probabilidad condicional antes de comprender en profundidad el Teorema de Bayes.

La probabilidad condicional

La probabilidad condicional se puede definir como la probabilidad de un evento o resultado basado en la ocurrencia de un evento o resultado anterior. Se calcula multiplicando la probabilidad del evento anterior por la probabilidad del evento posterior o condicional.

Veamos un ejemplo para entender mejor el concepto .

• El evento A es que una familia que planea una excursión irá de picnic. Hay un 80% de posibilidades de que la familia vaya al picnic.
• El evento B es que lloverá el día que la familia salga de picnic. El pronóstico del tiempo dice que hay un 60% de probabilidad de precipitaciones el día del picnic.
• Por lo tanto, la probabilidad (P) de que la familia vaya de picnic y llueva se calcula de la siguiente manera:

P (Picnic y lluvia) = P (Lluvia | Picnic) P (Picnic) = (0,60) * (0,80) = 0,48

En el ejemplo anterior, la probabilidad condicional analiza los dos eventos A y B en relación entre sí, es decir, la probabilidad de que la familia vaya de picnic y también llueva el mismo día.

Por lo tanto, la probabilidad condicional difiere de la probabilidad incondicional porque esta última se refiere a la probabilidad de que ocurra un evento independientemente de si ha tenido lugar otro evento o eventos o si hay otras condiciones presentes.

La fórmula de la probabilidad condicional

La fórmula para la probabilidad condicional proviene de la regla de multiplicación de probabilidad:

P (A y B) o P (AUB) = P ( B dado A) o P (B | A) * P (A)

En la ecuación anterior, P (A y B) es la probabilidad conjunta, que se refiere a la posibilidad de que dos o más eventos ocurran simultáneamente. También se escribe como P (A,B).

Aquí se explica cómo deducir la ecuación de probabilidad condicional de la regla de la multiplicación:

Paso 1: Escribe la regla de la multiplicación.

P (A y B) = P (B | A) * P (A)

Paso 2: Divide ambos lados de la ecuación por P (A).

P (A y B) / P (A) = P (B | A) * P (A) / P (A)

Paso 3: Cancele P (A) en el lado derecho de la ecuación.

P (A y B) / P (A) = P (B | A)

Paso 4: Reescribe la ecuación.

P (A y B) = P (B | A) / P (A)

Por lo tanto, la fórmula para la probabilidad condicional se da como:

P (A y B) = P (B | A) / P (A)

Teorema de Bayes

Usando el Teorema de Bayes, podemos actualizar nuestras creencias y convicciones en base a pruebas nuevas y relevantes. Por ejemplo, si estamos tratando de calcular la probabilidad de que una persona determinada tenga cáncer, generalmente supondremos que es el porcentaje de la población que tiene cáncer. Sin embargo, si introducimos evidencia extra, como que la persona en cuestión sea un fumador habitual, podemos actualizar nuestra percepción (y por lo tanto la probabilidad) ya que la probabilidad de tener cáncer es mayor si un individuo es fumador. Por lo tanto, utilizamos tanto nuestro conocimiento previo como la evidencia adicional para mejorar nuestras estimaciones.

La fórmula del teorema de Bayes

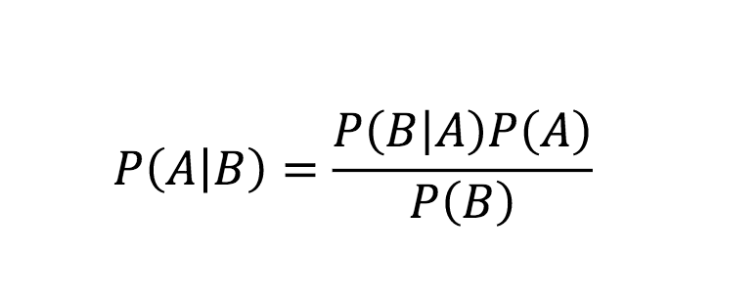
Fuente

La ecuación anterior es la regla de Bayes. Ahora, echemos un vistazo a la derivación paso a paso de la ecuación del Teorema de Bayes.

Paso 1: Considere dos eventos, A y B. A es el evento cuya probabilidad queremos calcular y B es la evidencia adicional relacionada con A.

Paso 2: Escriba la relación entre la probabilidad conjunta y la probabilidad condicional de los eventos A y B.

PAG (A, B) = PAG (A | B) * PAG (B) = PAG (B, A) = PAG (B | A) * PAG (A)

Paso 3: Establecer los dos términos de probabilidad condicional iguales entre sí.

PAG (A | B) * PAG (B) = PAG (B | A) * PAG (A)

Paso 4: Divide ambos lados de la ecuación por P (B).

P (A | B) * P (B) / P (B) = P (B | A) * P (A) / P (B)

Paso 5: Cancele P (B) en el lado izquierdo de la ecuación.

PAG (A | B) = PAG (B | A) * PAG (A) / PAG (B)

Por lo tanto, obtenemos la fórmula del Teorema de Bayes de la siguiente manera:

PAG (A | B) = PAG (B | A) * PAG (A) / PAG (B)

Comprender los términos en la ecuación del teorema de Bayes

PAG (A | B) = PAG (B | A) * PAG (A) / PAG (B)

• P (A | B) se llama la probabilidad posterior o la probabilidad que estamos tratando de estimar. En base al ejemplo anterior, la probabilidad posterior sería la probabilidad de que la persona tenga cáncer, dado que la persona es fumadora habitual.
• P (B | A) se llama probabilidad , y se refiere a la probabilidad de detectar la evidencia adicional, dada nuestra hipótesis inicial. En el ejemplo anterior, la probabilidad es la probabilidad de que la persona sea fumadora, dado que la persona tiene cáncer.
• P (A) es la probabilidad previa o la probabilidad de nuestra hipótesis sin ninguna evidencia o información adicional. En el ejemplo anterior, la probabilidad previa es la probabilidad de tener cáncer.
• P (B) es la probabilidad marginal o la probabilidad total de observar la evidencia. En el contexto del ejemplo anterior, la probabilidad marginal es la probabilidad de ser fumador.

Un ejemplo simple para entender el teorema de Bayes

Usando algunos números hipotéticos del ejemplo anterior, veremos el efecto de aplicar el Teorema de Bayes.

Supongamos que la probabilidad de tener cáncer es 0,06, es decir, el 6% de las personas tienen cáncer. Ahora, digamos que la probabilidad de ser fumador es 0.20 o el 20% de las personas son fumadores, y el 30% de las personas con cáncer son fumadores. Entonces, P (Fumador | Cáncer) = 0.30.

Inicialmente, la probabilidad de tener cáncer es simplemente 0,06 (previa). Pero usando la nueva evidencia, podemos calcular P (Cáncer | Fumador) = P ((Fumador | Cáncer) * P (Cáncer)) / P (Fumador) = (0.30*0.06) / (0.20) = 0.09.

Aprenda cursos de ciencia de datos en línea de las mejores universidades del mundo. Obtenga programas Executive PG, programas de certificados avanzados o programas de maestría para acelerar su carrera.

Camino a seguir: Domine los conceptos de estadística para una carrera en ciencia de datos o aprendizaje automático

La plataforma de aprendizaje EdTech superior de upGrad ha impactado a más de 500 000 profesionales que trabajan en todo el mundo con su gran cantidad de cursos y experiencias de aprendizaje inmersivo. Con una base de más de 40 000 estudiantes repartidos en más de 85 países, los cursos relevantes para la industria de upGrad están garantizados para avanzar en su carrera en el campo de su elección.

La Maestría en Ciencias en Ciencia de Datos es un curso de 18 meses que imparte habilidades clave en Estadística, Análisis Predictivo, Aprendizaje Automático, Análisis de Big Data, Visualización de Datos, etc.

Puntos destacados del programa:

• Maestría de la Universidad John Moores de Liverpool y PGP Ejecutivo de IIIT Bangalore
• Más de 500 horas de contenido, más de 60 estudios de casos y proyectos, más de 20 sesiones en vivo, más de 14 lenguajes de programación y herramientas
• Redes de la industria, sesiones de resolución de dudas y apoyo al aprendizaje.

El Programa de Certificado Avanzado en Aprendizaje Automático y Aprendizaje Profundo es un curso riguroso de 6 meses con oportunidades de trabajo en red entre pares, proyectos prácticos, tutoría de la industria y asistencia profesional de 360 ​​grados.

Puntos destacados del programa:

• Prestigioso reconocimiento del IIIT Bangalore
• Más de 240 horas de contenido, más de 5 estudios de casos y proyectos, más de 24 sesiones en vivo, cobertura de 12 lenguajes de programación, herramientas y bibliotecas
• Sesiones de coaching grupales 1:8 y sesiones de tutoría 1:1 con expertos de la industria

Conclusión

El pensamiento bayesiano sustenta varias áreas del pensamiento, la investigación y las creencias humanas, aunque la mayoría de nosotros no somos conscientes de ello. Desde la detección del cáncer y el calentamiento global hasta la política monetaria y la evaluación de riesgos y seguros , el pensamiento bayesiano es fundamental. Incluso se cree que el famoso matemático británico Alan Turing empleó el enfoque bayesiano para descifrar el Código Enigma alemán durante la Segunda Guerra Mundial.

¡Regístrese en upGrad y aumente su conocimiento de conceptos estadísticos clave y más!