Regresión polinomial: importancia, implementación paso a paso

Introducción

En este vasto campo del Machine Learning, ¿cuál sería el primer algoritmo que la mayoría de nosotros habríamos estudiado? Sí, es la regresión lineal. Siendo principalmente el primer programa y algoritmo que uno habría aprendido en sus primeros días de programación de aprendizaje automático, la regresión lineal tiene su propia importancia y poder con un tipo de datos lineal.

¿Qué sucede si el conjunto de datos con el que nos encontramos no es linealmente separable? ¿Qué pasa si el modelo de regresión lineal no puede derivar ningún tipo de relación entre las variables independientes y dependientes?

Viene otro tipo de regresión conocido como Regresión Polinomial. Fiel a su nombre, Polynomial Regression es un algoritmo de regresión que modela la relación entre la variable dependiente (y) y la variable independiente (x) como un polinomio de grado n. En este artículo, comprenderemos el algoritmo y las matemáticas detrás de la regresión polinomial junto con su implementación en Python.

¿Qué es la regresión polinomial?

Como se definió anteriormente, la regresión polinomial es un caso especial de regresión lineal en el que una ecuación polinomial con un grado (n) especificado se ajusta a los datos no lineales que forman una relación curvilínea entre las variables dependientes e independientes.

y= segundo 0 + segundo 1 x 1 + segundo 2 x 1 2 + segundo 3 x 1 3 +…… segundo norte x 1 norte

Aquí,

y es la variable dependiente (variable de salida)

x1 es la variable independiente (predictores)

b 0 es el sesgo

b 1 , b 2 , ….b n son los pesos en la ecuación de regresión.

A medida que aumenta el grado de la ecuación polinomial ( n ), la ecuación polinomial se vuelve más complicada y existe la posibilidad de que el modelo tienda a sobreajustarse, lo que se discutirá en la parte posterior.

Comparación de ecuaciones de regresión

Regresión lineal simple ===> y= b0+b1x

Regresión lineal múltiple ===> y= b0+b1x1+ b2x2+ b3x3+…… bnxn

Regresión polinomial ===> y= b0+b1x1+ b2x12+ b3x13+…… bnx1n

De las tres ecuaciones anteriores, vemos que hay varias diferencias sutiles en ellas. Las regresiones lineales simple y múltiple se diferencian de la ecuación de regresión polinomial en que tiene un grado de solo 1. La regresión lineal múltiple consta de varias variables x1, x2, etc. Aunque la ecuación de regresión polinomial tiene solo una variable x1, tiene un grado n que la diferencia de las otras dos.

Necesidad de regresión polinomial

En los diagramas a continuación, podemos ver que en el primer diagrama, se intenta ajustar una línea lineal en el conjunto dado de puntos de datos no lineales. Se entiende que se vuelve muy difícil que una línea recta forme una relación con estos datos no lineales. Debido a esto, cuando entrenamos el modelo, la función de pérdida aumenta provocando el alto error.

Por otro lado, cuando aplicamos la regresión polinomial, es claramente visible que la línea se ajusta bien a los puntos de datos. Esto significa que la ecuación polinomial que se ajusta a los puntos de datos deriva algún tipo de relación entre las variables del conjunto de datos. Por lo tanto, para los casos en los que los puntos de datos se organizan de forma no lineal, necesitamos el modelo de regresión polinomial.

Implementación de regresión polinomial en Python

A partir de aquí, construiremos un modelo de aprendizaje automático en Python que implemente la regresión polinomial. Compararemos los resultados obtenidos con la Regresión Lineal y la Regresión Polinomial. Entendamos primero el problema que vamos a resolver con la regresión polinomial.

Descripción del problema

En esto, considere el caso de una Start-up que busca contratar a varios candidatos de una empresa. Hay diferentes vacantes para diferentes puestos de trabajo en la empresa. La puesta en marcha tiene detalles del salario para cada función en la empresa anterior. Así, cuando un candidato menciona su salario anterior, el RRHH de la start-up necesita verificarlo con los datos existentes. Así, tenemos dos variables independientes que son Posición y Nivel. La variable dependiente (salida) es el salario que se va a predecir mediante la regresión polinomial.

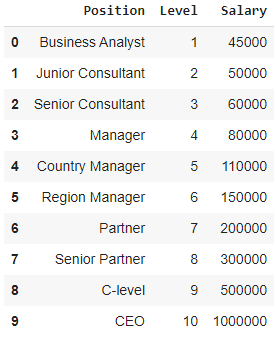
Al visualizar la tabla anterior en un gráfico, vemos que los datos son de naturaleza no lineal. En otras palabras, a medida que aumenta el nivel, el salario aumenta a una tasa más alta, lo que nos da una curva como la que se muestra a continuación.

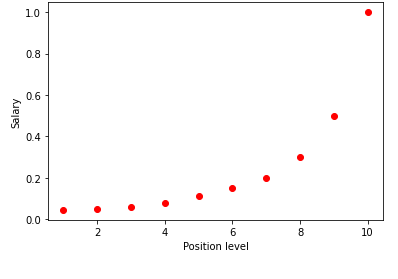
Paso 1: Preprocesamiento de datosEl primer paso para construir cualquier modelo de Machine Learning es importar las bibliotecas. Aquí, solo tenemos tres bibliotecas básicas para importar. Después de esto, el conjunto de datos se importa desde mi repositorio de GitHub y se asignan las variables dependientes y las variables independientes. Las variables independientes se almacenan en la variable X y la variable dependiente se almacena en la variable y.

importar numpy como np

importar matplotlib.pyplot como plt

importar pandas como pd

conjunto de datos = pd.read_csv('https://raw.githubusercontent.com/mk-gurucharan/Regression/master/PositionSalaries_Data.csv')

X = conjunto de datos.iloc[:, 1:-1].valores

y = conjunto de datos.iloc[:, -1].valores

Aquí, en el término [:, 1:-1], los primeros dos puntos representan que se deben tomar todas las filas y el término 1:-1 denota que las columnas que se incluirán van desde la primera columna hasta la penúltima columna, lo que viene dado por -1.

Paso 2: Modelo de regresión linealEn el próximo paso, construiremos un modelo de Regresión Lineal Múltiple y lo usaremos para predecir los datos salariales de las variables independientes. Para ello se importa la clase LinearRegression de la librería sklearn. Luego se ajusta a las variables X e y con fines de entrenamiento.

de sklearn.linear_model importar LinearRegression

regresor = LinearRegression()

regresor.fit(X, y)

Una vez construido el modelo, al visualizar los resultados, obtenemos el siguiente gráfico.

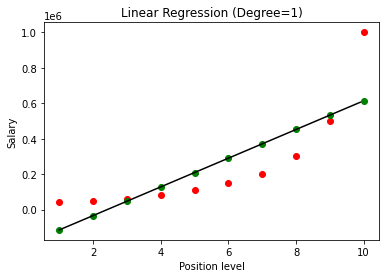
Como se ve claramente, al tratar de ajustar una línea recta en un conjunto de datos no lineal, el modelo de aprendizaje automático no deriva ninguna relación. Por lo tanto, debemos optar por la regresión polinomial para obtener una relación entre las variables.

Paso 3: Modelo de regresión polinomialEn este próximo paso, ajustaremos un modelo de regresión polinomial en este conjunto de datos y visualizaremos los resultados. Para esto importamos otra Clase del módulo sklearn llamada PolynomialFeatures en la cual damos el grado de la ecuación polinomial a construir. Luego, la clase LinearRegression se usa para ajustar la ecuación polinomial al conjunto de datos.

de sklearn.preprocessing import PolynomialFeatures

de sklearn.linear_model importar LinearRegression

poly_reg = PolynomialFeatures (grado = 2)

X_poly = poly_reg.fit_transform(X)

lin_reg = Regresión Lineal()

lin_reg.fit(X_poli, y)

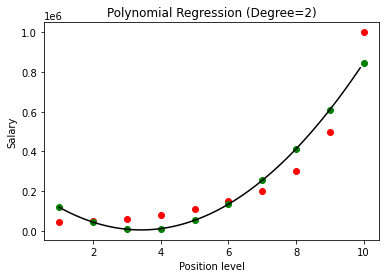
En el caso anterior, hemos dado el grado de la ecuación polinomial para que sea igual a 2. Al trazar el gráfico, vemos que hay algún tipo de curva que se deriva pero aún hay mucha desviación de los datos reales (en rojo ) y los puntos de la curva previstos (en verde). Por lo tanto, en el siguiente paso aumentaremos el grado del polinomio a números más altos, como 3 y 4, y luego lo compararemos entre sí.

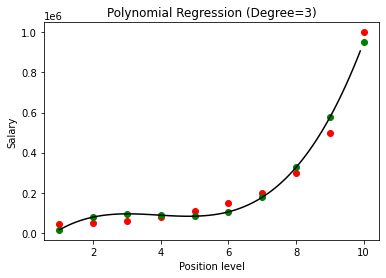
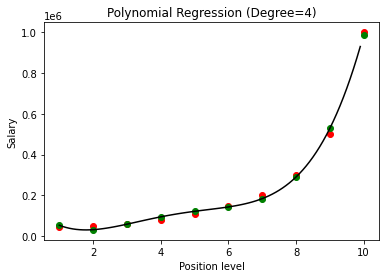
Al comparar los resultados de la Regresión Polinomial con los grados 3 y 4, vemos que a medida que aumenta el grado, el modelo entrena bien con los datos. Por lo tanto, podemos inferir que un grado más alto permite que la ecuación polinomial se ajuste con mayor precisión a los datos de entrenamiento. Sin embargo, este es el caso perfecto de overfitting. Por lo tanto, se vuelve importante elegir el valor de n precisamente para evitar el sobreajuste.

¿Qué es el sobreajuste?

Como su nombre indica, el sobreajuste se denomina una situación estadística en la que una función (o un modelo de aprendizaje automático en este caso) se ajusta demasiado a un conjunto de puntos de datos limitados. Esto hace que la función funcione mal con nuevos puntos de datos.

En Machine Learning, si se dice que un modelo se ajusta demasiado a un conjunto determinado de puntos de datos de entrenamiento, cuando el mismo modelo se introduce en un conjunto de puntos completamente nuevo (por ejemplo, el conjunto de datos de prueba), se comporta muy mal como el el modelo de sobreajuste no se ha generalizado bien con los datos y solo se sobreajusta en los puntos de datos de entrenamiento.

En la regresión polinomial, existe una buena posibilidad de que el modelo se sobreajuste en los datos de entrenamiento a medida que aumenta el grado del polinomio. En el ejemplo que se muestra arriba, vemos un caso típico de sobreajuste en la regresión polinomial que se puede corregir con solo una base de prueba y error para elegir el valor óptimo del grado.

Lea también: Ideas de proyectos de aprendizaje automático

Conclusión

Para concluir, la regresión polinomial se utiliza en muchas situaciones en las que existe una relación no lineal entre las variables dependientes e independientes. Aunque este algoritmo sufre de sensibilidad hacia los valores atípicos, se puede corregir tratándolos antes de ajustar la línea de regresión. Por lo tanto, en este artículo, se nos presentó el concepto de regresión polinomial junto con un ejemplo de su implementación en la programación de Python en un conjunto de datos simple.

Si está interesado en obtener más información sobre el aprendizaje automático, consulte el Diploma PG en aprendizaje automático e IA de IIIT-B y upGrad, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, IIIT- B Estado de exalumno, más de 5 proyectos prácticos finales prácticos y asistencia laboral con las mejores empresas.

Aprenda el curso ML de las mejores universidades del mundo. Obtenga programas de maestría, PGP ejecutivo o certificado avanzado para acelerar su carrera.

¿A qué te refieres con regresión lineal?

La regresión lineal es un tipo de análisis numérico predictivo a través del cual podemos encontrar el valor de una variable desconocida con la ayuda de una variable dependiente. También explica la conexión entre una variable dependiente y una o más independientes. La regresión lineal es una técnica estadística para demostrar un vínculo entre dos variables. La regresión lineal traza una línea de tendencia a partir de un conjunto de puntos de datos. La regresión lineal se puede utilizar para generar un modelo de predicción a partir de datos aparentemente aleatorios, como diagnósticos de cáncer o precios de acciones. Hay varios métodos para calcular la regresión lineal. El enfoque de mínimos cuadrados ordinarios, que estima variables desconocidas en los datos y las transforma visualmente en la suma de las distancias verticales entre los puntos de datos y la línea de tendencia, es uno de los más frecuentes.

¿Cuáles son algunos de los inconvenientes de la regresión lineal?

En la mayoría de los casos, el análisis de regresión se utiliza en la investigación para establecer que existe un vínculo entre las variables. Sin embargo, la correlación no implica causalidad, ya que un vínculo entre dos variables no implica que una provoque que suceda la otra. Incluso una línea en una regresión lineal básica que se adapte bien a los puntos de datos puede no garantizar una relación entre las circunstancias y los resultados lógicos. Usando un modelo de regresión lineal, puede determinar si existe o no alguna correlación entre las variables. Se requerirá una investigación adicional y un análisis estadístico para determinar la naturaleza exacta del vínculo y si una variable causa la otra.

¿Cuáles son los supuestos básicos de la regresión lineal?

En la regresión lineal, hay tres suposiciones clave. Las variables dependientes e independientes deben, ante todo, tener una conexión lineal. Se utiliza un diagrama de dispersión de las variables dependientes e independientes para verificar esta relación. En segundo lugar, debe haber una multicolinealidad mínima o nula entre las variables independientes del conjunto de datos. Implica que las variables independientes no están relacionadas. El valor debe ser limitado, lo cual está determinado por el requisito de dominio. La homocedasticidad es el tercer factor. La suposición de que los errores se distribuyen uniformemente es una de las suposiciones más esenciales.