Aprenda el algoritmo Naive Bayes para el aprendizaje automático [con ejemplos]
Publicado: 2021-02-25Tabla de contenido
Introducción
En matemáticas y programación, algunas de las soluciones más simples suelen ser las más poderosas. El ingenuo Algoritmo de Bayes viene como un ejemplo clásico de esta afirmación. Incluso con el fuerte y rápido avance y desarrollo en el campo del aprendizaje automático, este algoritmo Naive Bayes sigue siendo uno de los algoritmos más utilizados y eficientes. El algoritmo de Bayes ingenuo encuentra sus aplicaciones en una variedad de problemas que incluyen tareas de clasificación y problemas de procesamiento del lenguaje natural (NLP).
La hipótesis matemática del Teorema de Bayes sirve como el concepto fundamental detrás de este Algoritmo de Naive Bayes. En este artículo, repasaremos los conceptos básicos del teorema de Bayes, el algoritmo Naive Bayes junto con su implementación en Python con un problema de ejemplo en tiempo real. Junto con estos, también veremos algunas ventajas y desventajas del algoritmo Naive Bayes en comparación con sus competidores.
Conceptos básicos de probabilidad
Antes de aventurarnos a comprender el Teorema de Bayes y el Algoritmo de Naive Bayes, repasemos nuestro conocimiento existente sobre los fundamentos de la Probabilidad.
Como todos sabemos por definición, dado un evento A, la probabilidad de que ese evento ocurra viene dada por P(A). En probabilidad, dos eventos A y B se denominan eventos independientes si la ocurrencia del evento A no altera la probabilidad de ocurrencia del evento B y viceversa. Por otro lado, si la ocurrencia de uno cambia la probabilidad del otro, entonces se denominan eventos dependientes.
Conozcamos un nuevo término llamado probabilidad condicional . En matemáticas, la probabilidad condicional para dos eventos A y B dada por P (A | B) se define como la probabilidad de que ocurra el evento A dado que el evento B ya ocurrió. Dependiendo de la relación entre los dos eventos A y B en cuanto a si son dependientes o independientes, la probabilidad condicional se calcula de dos maneras.
- La probabilidad condicional de dos eventos dependientes A y B viene dada por P (A| B) = P (A y B) / P (B)
- La expresión para la probabilidad condicional de dos eventos independientes A y B está dada por, P (A| B) = P (A)
Conociendo las matemáticas detrás de la Probabilidad y las Probabilidades Condicionales, pasemos ahora al Teorema de Bayes.

Teorema de Bayes
En estadística y teoría de la probabilidad, el teorema de Bayes, también conocido como la regla de Bayes, se utiliza para determinar la probabilidad condicional de los eventos. En otras palabras, el teorema de Bayes describe la probabilidad de un evento con base en el conocimiento previo de las condiciones que podrían ser relevantes para el evento.
Para entenderlo de una manera más sencilla, considera que necesitamos saber la probabilidad de que el precio de una casa sea muy alto. Si conocemos los otros parámetros, como la presencia de escuelas, tiendas médicas y hospitales cercanos, entonces podemos hacer una evaluación más precisa de los mismos. Esto es exactamente lo que realiza el Teorema de Bayes.
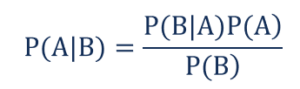
tal que,
- P(A|B): la probabilidad condicional de que ocurra el evento A, dado que ha ocurrido el evento B, también conocida como probabilidad posterior .
- P(B|A) – la probabilidad condicional de que ocurra el evento B, dado que el evento A ha ocurrido, también conocido como probabilidad de verosimilitud .
- P (A): la probabilidad de que ocurra el evento A, también conocida como probabilidad previa.
- P (B): la probabilidad de que ocurra el evento B, también conocida como probabilidad marginal.
Supongamos que tenemos un problema simple de aprendizaje automático con 'n' variables independientes y la variable dependiente que es la salida es un valor booleano (verdadero o falso). Supongamos que los atributos independientes son de naturaleza categórica. Consideremos 2 categorías para este ejemplo. Por lo tanto, con estos datos, necesitamos calcular el valor de la Probabilidad de Verosimilitud, P(B|A).
Por lo tanto, al observar lo anterior, encontramos que necesitamos calcular 2*(2^ n -1 ) parámetros para poder aprender este modelo de Machine Learning. De manera similar, si tenemos 30 atributos booleanos independientes, entonces el número total de parámetros a calcular será cercano a los 3 mil millones, lo cual es un costo computacional extremadamente alto.
Esta dificultad para construir un modelo de Machine Learning con el Teorema de Bayes condujo al nacimiento y desarrollo del Algoritmo Naive Bayes.
Algoritmo bayesiano ingenuo
Para que sea práctico, la complejidad del teorema de Bayes antes mencionada debe reducirse. Esto se logra exactamente en el Algoritmo Naive Bayes haciendo algunas suposiciones. Las suposiciones hechas son que cada característica hace una contribución independiente e igual al resultado.
El algoritmo de Bayes ingenuo es un algoritmo de aprendizaje supervisado y se basa en el teorema de Bayes, que se utiliza principalmente para resolver problemas de clasificación. Es uno de los clasificadores más simples y precisos que construye modelos de aprendizaje automático para hacer predicciones rápidas. Matemáticamente es un clasificador probabilístico ya que realiza predicciones utilizando la función de probabilidad de los eventos.
Problema de ejemplo
Para comprender la lógica detrás de las suposiciones, analicemos un conjunto de datos simple para obtener una mejor intuición.
| Color | Escribe | Origen | ¿Hurto? |
| Negro | Sedán | Importado | sí |
| Negro | todoterreno | Importado | No |
| Negro | Sedán | Doméstico | sí |
| Negro | Sedán | Importado | No |
| marrón | todoterreno | Doméstico | sí |
| marrón | todoterreno | Doméstico | No |
| marrón | Sedán | Importado | No |
| marrón | todoterreno | Importado | sí |
| marrón | Sedán | Doméstico | No |
Del conjunto de datos anterior, podemos derivar los conceptos de las dos suposiciones que definimos para el Algoritmo Naive Bayes anterior.
- La primera suposición es que todas las características son independientes entre sí. Aquí vemos que cada atributo es independiente como el color “Rojo” es independiente del Tipo y Origen del auto.
- A continuación, a cada característica se le debe dar la misma importancia. De manera similar, solo tener conocimiento sobre el tipo y el origen del automóvil no es suficiente para predecir el resultado del problema. Por lo tanto, ninguna de las variables es irrelevante y, por lo tanto, todas contribuyen por igual al resultado.
En resumen, A y B son condicionalmente independientes dado C si y sólo si, dado el conocimiento de que C ocurre, el conocimiento de si A ocurre no proporciona información sobre la probabilidad de que B ocurra, y el conocimiento de si B ocurre no proporciona información sobre la probabilidad de que ocurra A. Estas suposiciones hacen que el algoritmo de Bayes sea Naive . De ahí el nombre, Algoritmo Naive Bayes.
Por lo tanto, para el problema anterior, el teorema de Bayes se puede reescribir como:
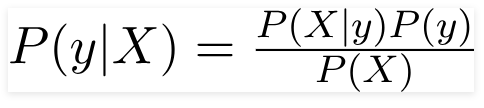
tal que,
- El vector de características independiente, X = (x 1 , x 2 , x 3 ……x n ) que representa las características como el color, el tipo y el origen del automóvil.
- La variable de salida, y tiene solo dos resultados Sí o No.
Por lo tanto, al sustituir los valores anteriores, obtenemos la fórmula de Naive Bayes como,
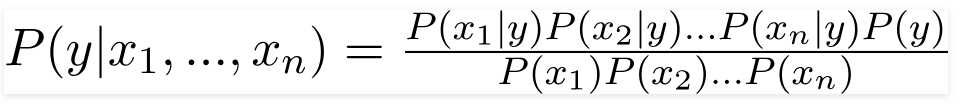
Para calcular la probabilidad posterior P(y|X), tenemos que crear una tabla de frecuencias para cada atributo contra la salida. Luego, convertimos las tablas de frecuencia en tablas de probabilidad, después de lo cual finalmente usamos la ecuación bayesiana ingenua para calcular la probabilidad posterior para cada clase. La clase con la probabilidad posterior más alta se elige como el resultado de la predicción. A continuación se encuentran las tablas de frecuencia y probabilidad para los tres predictores.
Tabla de frecuencia de color Tabla de probabilidad de color
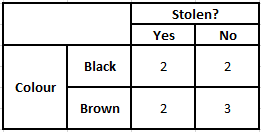
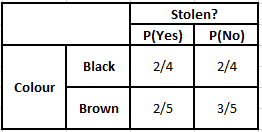
Tabla de frecuencia de tipo Tabla de probabilidad de tipo
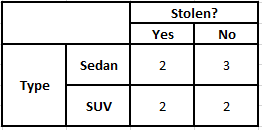
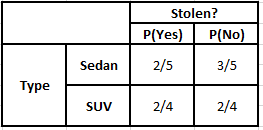

Frecuencia Tabla de origen Probabilidad Tabla de origen
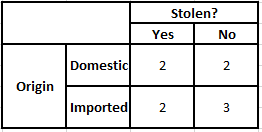
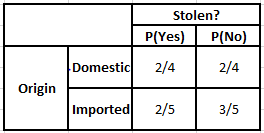
Considere el caso en el que necesitamos calcular las probabilidades posteriores para las condiciones dadas a continuación:
| Color | Escribe | Origen |
| marrón | todoterreno | Importado |
Por lo tanto, a partir de la fórmula anterior, podemos calcular las probabilidades posteriores como se muestra a continuación:
P(Sí | X) = P(Marrón | Sí) * P(SUV | Sí) * P(Importado | Sí) * P(Sí)
= 2/5 * 2/4 * 2/5 * 1
= 0,08
P(No | X) = P(Marrón | No) * P(SUV | No) * P(Importado | No) * P(No)
= 3/5 * 2/4 * 3/5 * 1
= 0,18
De los valores calculados anteriormente, como las Probabilidades Posteriores para No son Mayores que Sí (0.18>0.08), entonces se puede inferir que un automóvil con Color Marrón, Tipo SUV de Origen Importado se clasifica como “No”. Por lo tanto, el coche no es robado.
Implementación en Python
Ahora que hemos entendido las matemáticas detrás del algoritmo Naive Bayes y también lo hemos visualizado con un ejemplo, veamos su código de aprendizaje automático en lenguaje Python.
Relacionado: Clasificador Naive Bayes
Análisis del problema
Para implementar el programa Naive Bayes Classification en Machine Learning usando Python, usaremos el muy famoso 'Iris Flower Dataset'. El conjunto de datos de flores de Iris o el conjunto de datos de Iris de Fisher es un conjunto de datos multivariado introducido por el estadístico, eugenista y biólogo británico Ronald Fisher en 1998. Este es un conjunto de datos muy pequeño y básico que consiste en datos muy menos numéricos que contienen información sobre 3 clases de flores pertenecientes a la especie Iris que son:
- Iris Setosa
- Iris Versicolor
- iris virginica
Hay 50 muestras de cada una de las tres especies que suman un conjunto de datos total de 150 filas. Los 4 atributos (o) variables independientes que se utilizan en este conjunto de datos son:
- longitud del sépalo en cm
- anchura del sépalo en cm
- longitud del pétalo en cm
- ancho de pétalo en cm
La variable dependiente es la " especie " de la flor que se identifica por los cuatro atributos dados anteriormente.
Paso 1: importar las bibliotecas
Como siempre, el paso principal en la construcción de cualquier modelo de Machine Learning será importar las bibliotecas relevantes. Para ello, cargaremos las librerías NumPy, Mathplotlib y Pandas para preprocesar los datos.
importar numpy como np
importar matplotlib.pyplot como plt
importar pandas como pd
Paso 2: cargar el conjunto de datos
El conjunto de datos de flores de Iris que se usará para entrenar el clasificador Naive Bayes se cargará en un marco de datos de Pandas. Las 4 variables independientes se asignarán a la variable X y la variable de especie de salida final se asignará a y.
conjunto de datos = pd.read_csv(' https://raw.githubusercontent.com/mk-gurucharan/Classification/master/IrisDataset.csv' )X = conjunto de datos.iloc[:,:4].valores
y = conjunto de datos['especies'].valoresconjuntodedatos.head(5)>>
longitud_del_sépalo anchura_del_sépalo longitud_del_pétalo anchura_del_pétalo especie
5.1 3.5 1.4 0.2 setosa
4,9 3,0 1,4 0,2 setosa
4,7 3,2 1,3 0,2 setosa
4,6 3,1 1,5 0,2 setosa
5,0 3,6 1,4 0,2 setosa
Paso 3: dividir el conjunto de datos en el conjunto de entrenamiento y el conjunto de prueba
Después de cargar el conjunto de datos y las variables, el siguiente paso es preparar las variables que se someterán al proceso de entrenamiento. En este paso, tenemos que dividir las variables X e Y en los conjuntos de datos de entrenamiento y prueba. Para ello, asignaremos aleatoriamente el 80 % de los datos al conjunto de entrenamiento que se utilizará con fines de entrenamiento y el 20 % restante de los datos como conjunto de prueba en el que se probará la precisión del clasificador Naive Bayes entrenado.
de sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size = 0.2)
Paso 4: Escalado de funciones
Aunque este es un proceso adicional a este pequeño conjunto de datos, lo agrego para que lo use en un conjunto de datos más grande. En esto, los datos en los conjuntos de entrenamiento y prueba se reducen a un rango de valores entre 0 y 1. Esto reduce el costo computacional.
de sklearn.preprocessing importar StandardScaler
sc = escalador estándar()
tren_X = sc.fit_transform(tren_X)
X_test = sc.transform(X_test)
Paso 5: entrenar el modelo de clasificación Naive Bayes en el conjunto de entrenamiento
Es en este paso que importamos la clase Naive Bayes de la biblioteca sklearn. Para este modelo, usamos el modelo Gaussiano, hay varios otros modelos como Bernoulli, Categorical y Multinomial. Por lo tanto, X_train y y_train se ajustan a la variable clasificadora con fines de entrenamiento.
de sklearn.naive_bayes importar GaussianNB
clasificador = GaussianNB()
clasificador.fit(tren_X, tren_y)
Paso 6: predicción de los resultados del conjunto de pruebas:
Predecimos la clase de la especie para el conjunto de prueba utilizando el modelo entrenado y lo comparamos con los valores reales de la clase de especie.
y_pred = clasificador.predecir(X_test)
df = pd.DataFrame({'Valores reales':y_test, 'Valores previstos':y_pred})
df>>
Valores reales Valores pronosticados
setosa setosa
setosa setosa
virginica virginica
versicolor versicolor
setosa setosa
setosa setosa
… … … … …
virgen versicolor
virginica virginica
setosa setosa
setosa setosa
versicolor versicolor
versicolor versicolor
En la comparación anterior, vemos que hay una predicción incorrecta que ha predicho Versicolor en lugar de virginica.
Paso 7 – Matriz de confusión y precisión
Como nos ocupamos de la clasificación, la mejor manera de evaluar nuestro modelo de clasificador es imprimir la matriz de confusión junto con su precisión en el conjunto de prueba.
de sklearn.metrics importar confusion_matrix
cm = confusion_matrix(y_test, y_pred)de sklearn.metrics import precision_score

imprimir ("Precisión: ", precision_score(y_test, y_pred))
cm>>Precisión: 0.9666666666666667
>>matriz([[14, 0, 0],
[ 0, 7, 0],
[ 0, 1, 8]])
Conclusión
Por lo tanto, en este artículo, hemos repasado los conceptos básicos del Algoritmo Naive Bayes, entendido las matemáticas detrás de la Clasificación junto con un ejemplo resuelto a mano. Finalmente, implementamos un código de aprendizaje automático para resolver un conjunto de datos popular utilizando el algoritmo de clasificación Naive Bayes.
Si está interesado en obtener más información sobre IA, aprendizaje automático, consulte el Diploma PG de IIIT-B y upGrad en Aprendizaje automático e IA, que está diseñado para profesionales que trabajan y ofrece más de 450 horas de capacitación rigurosa, más de 30 estudios de casos y asignaciones, Estado de ex alumnos de IIIT-B, más de 5 proyectos prácticos finales y asistencia laboral con las mejores empresas.
¿Cómo es útil la probabilidad en el aprendizaje automático?
Es posible que tengamos que tomar decisiones basadas en información parcial o incompleta en escenarios del mundo real. La probabilidad nos ayuda a cuantificar las incertidumbres en dichos sistemas y gestionar el riesgo de la tarea. El método tradicional funciona solo para los resultados deterministas de acciones específicas, pero siempre hay cierto margen de incertidumbre en cualquier modelo de predicción. Esta incertidumbre puede provenir de muchos parámetros de los datos de entrada, como el ruido en los datos. Además, las vistas bayesianas de los teoremas de probabilidad pueden ayudar al reconocimiento de patrones a partir de los datos de entrada. Para esto, la probabilidad usa el concepto de estimación de máxima verosimilitud y, por lo tanto, es útil para producir resultados relevantes.
¿Cuál es el uso de la matriz de confusión?
La matriz de confusión es una matriz de 2x2 que se utiliza para interpretar el rendimiento del modelo de clasificación. Los valores verdaderos de los datos de entrada deben conocerse para que esto funcione, por lo que no se pueden representar para datos sin etiquetar. Consiste en el número de falsos positivos (FP), verdaderos positivos (TP), falsos negativos (FN) y verdaderos negativos (TN). Las predicciones se clasifican en estas clases utilizando el conteo del conjunto de entrenamiento y el conjunto de prueba. Nos ayuda a visualizar parámetros útiles como exactitud, precisión, recuperación y especificidad. Es relativamente fácil de entender y le da una idea clara sobre el algoritmo.
¿Cuáles son los diferentes tipos de modelo Naive Bayes?
Todos los tipos se basan principalmente en el teorema de Bayes. El modelo Naive Bayes generalmente tiene tres tipos: Gaussiano, Bernoulli y Multinomial. El Gaussian Naive Bayes ayuda con valores continuos de los parámetros de entrada, y asume que todas las clases de datos de entrada se distribuyen uniformemente. El ingenuo Bayes de Bernoulli es un modelo basado en eventos donde las características de los datos son independientes y están presentes en valores booleanos. Multinomial Naive Bayes también se basa en un modelo basado en eventos. Tiene las características de los datos en forma de vector, lo que representa frecuencias relevantes en función de la ocurrencia de los eventos.
